Что такое прямоугольник ромб квадрат какие свойства вы знаете
Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма.
Определение 2
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой.
Напомним основные свойства параллелограмма.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Рассмотрим далее подробно понятия прямоугольника, ромба и квадрата.
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
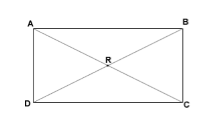
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $angle B=angle A={90}^0$, а $AB$ – общая сторона, то по I признаку равенства треугольников, $triangle ABD=triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $angle DRC=angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $triangle DRC=triangle ARB$. Значит, $angle RDC=angle RCD=angle RAB={rm }angle RBA$.
Так как $angle DRA=angle CRB$, как вертикальные, то по I признаку равенства треугольников $triangle DRA=triangle CRB$. Значит, $angle RDA=angle RAD=angle RCB={rm }angle RBC$.
Следовательно, $angle A=angle B=angle C=angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
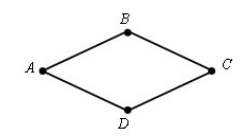
Рисунок 3. Ромб
Рассмотрим свойство ромба.
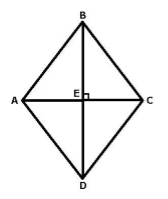
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).

Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ – медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).

Рисунок 5. Квадрат
Очевидно, что квадрат — частный случай ромба. Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.
Пример задачи
Пример 1
Найти периметр квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
[a^2+a^2=100] [{2a}^2=100] [a^2=50] [a=5sqrt{2}] [P=4a=20sqrt{2}]
Ответ: $20sqrt{2}$.
Источник
Инфоурок
›
Геометрия
›Презентации›Презентация по геометрии “Прямоугольник, ромб, квадрат” (8 кл)

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Учебное занятие по геометрии в 8 классе
2 слайд

Описание слайда:
Ввести определения прямоугольника, ромба, квадрата как частных видов параллелограмма, изучить их свойства и признаки, закрепить полученные знания при решении задач. Повторить, обобщить, систематизировать знания учащихся о параллелограммах. Цели учебного занятия:
3 слайд

Описание слайда:
Прямоугольник Ромб Квадрат Решение задач Тест
4 слайд

Описание слайда:
ПРЯМОУГОЛЬНИК Прямоугольник – это параллелограмм, у которого все углы прямые.
5 слайд

Описание слайда:
Свойства прямоугольника Диагонали прямоугольника равны Диагонали прямоугольника точкой пересечения делятся пополам В прямоугольнике противоположные стороны равны
6 слайд

Описание слайда:
Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
7 слайд

Описание слайда:
РОМБ Ромб – это параллелограмм, у которого все стороны равны.
8 слайд

Описание слайда:
Слово ромб произошло от греческого слова rombos – “бубен”. Впервые термин употребляется у древнегреческих учёных Герона и Паппа Александрийского
9 слайд

Описание слайда:
СВОЙСТВА РОМБА Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам. Диагонали ромба являются биссектрисами его углов.
10 слайд

Описание слайда:
ПРИЗНАК РОМБА Параллелограмм является ромбом, если его диагонали взаимно перпендикулярны.
11 слайд

Описание слайда:
КВАДРАТ Квадратом называется прямоугольник, у которого все стороны равны Квадратом называется ромб, у которого все углы прямые
12 слайд

Описание слайда:
Слово квадрат произошло от латинского слова quadratus – “четырехугольный” (от guattuor – “четыре”). Квадратом также называют возведение в степень 2 χ² 3² Y² 5²
13 слайд

Описание слайда:
СВОЙСТВА КВАДРАТА Все углы квадрата прямые. Диагонали квадрата равны. Диагонали квадрата взаимно перпендикулярны, точкой пересечения делятся пополам. Диагонали квадрата делят углы квадрата пополам.
14 слайд

Описание слайда:
Решение задач: 1
15 слайд

16 слайд

17 слайд

18 слайд

Описание слайда:
Тест + + – 2. Все стороны равны + + + 3.Противолежащие углы равны + + – 7. Диагонали взаимно перпендикулярны + – + 6. Диагонали равны + + + 5. Диагонали пересекаются и точкой пересечения делятся пополам + – + 4. Все углы прямые + + + 1.Противолежащие стороны параллельны и равны Квадрат Ромб Прямоугольник Да – «+» Нет – «-»
19 слайд

Описание слайда:
Задача 1. Диагонали прямоугольника АВСD пересекаются в точке О, АВО = 36. Найдите АОD. Задача 2. Найдите периметр ромба ABCD, если В = 120, а BD=8 см. Задача 3. Периметр ромба ABCD равен 16 см. Высота, опущенная к стороне AD из вершины B, равна 2 см. Найдите углы ромба. Домашнее задание – На выбор можно решить любые две задачи.
20 слайд

Описание слайда:
Как только бросили нам клич Мы все тут тотчас собрались. Я – параллелограмм Важнее всех фигур, Я всех их свойствами своими наделил. Но их достоинств я не смею умалить Ведь место в геометрии и есть для них. Хоть стороны мои попарно и равны и параллельны, Всё же я в печали, что не равны мои диагонали, Да и углы они не делят пополам.
21 слайд

Описание слайда:
А я – особый параллелограмм, Все стороны мои наклонены, Да и к тому же все равны. Меня за это ромбом величают, Геометрической фигурой называют Диагонали под прямым углом пройдут, Они же тотчас пополам углы разделят На части равные фигуру разобьют.
22 слайд

Описание слайда:
А я – прямоугольник, В отличии от всех Все стороны свои держу я строго, Две – чуть поменьше, ну а две – побольше, Которые напротив – те равны, А те, что смежные углом прямым скрепляю, И преимущество имею я: Ведь все ж равны мои диагонали.
23 слайд

Описание слайда:
Рекомендуюсь: я квадрат. Любую площадь я замерить рад. С глубокой древности я – мера площадей, Она в квадрате стороны моей. Имею я четыре стороны. И все они равны. Но у меня притом равны диагонали, Углы они мне делят пополам, На части равные разбит я ими сам. Вобрав все важное в себя, Фигурой знатной стал и я.
24 слайд

Описание слайда:
А я фигура не похожая на всех. Хоть я и не параллелограмм. Но среди них мне место есть Ведь у меня же параллельны основания, Бывают стороны равны, диагонали, Ещё углы при основании, Тогда трапецией я равнобокую зовусь.
25 слайд

Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка – книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики

Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-308521
Вам будут интересны эти курсы:
Оставьте свой комментарий
Источник
Прямоугольник – параллелограмм, у которого все углы прямые.
Диагональю прямоугольника называется любой отрезок, соединяющий две вершины противоположных углов прямоугольника. Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Свойства прямоугольника
- Противоположные стороны прямоугольника равны.
- Каждый угол прямоугольника равен 90°.
- Значит, противоположные углы равны и сумма углов, прилежащих к одной стороне, равна 180°.
- Диагонали прямоугольника точкой пересечения делятся пополам.
- Диагональ прямоугольника делит его на два равных прямоугольных треугольника.
- Накрест лежащие углы при диагонали равны.
- Диагонали прямоугольника равны.
- Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности.
- Около любого прямоугольника можно описать окружность, при этом диагональ прямоугольника равна диаметру описанной окружности.
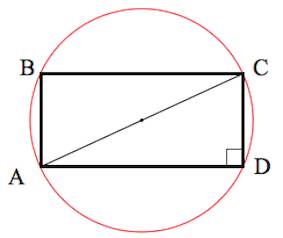
Признаки прямоугольника
- Если три угла четырехугольника прямые, то этот четырехугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны и для квадрата.
- Все четыре стороны квадрата имеют одинаковую длину, то есть они равны.
- Противоположные стороны квадрата параллельны.
- Сумма углов квадрата равна 360°.
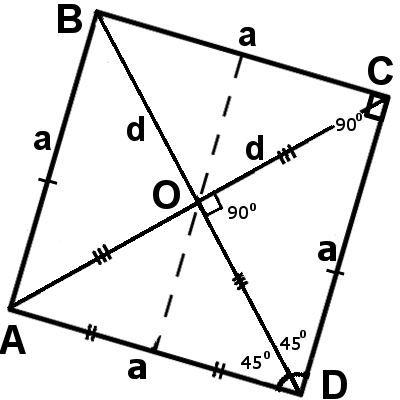
- Диагонали квадрата имеют одинаковые длины.
- Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружностей.
- Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные, и прямоугольные.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Формулы определения длины диагонали квадрата:
(d=asqrt{2}; d=sqrt{2S}; d=2R; d=2rsqrt{2}).
Ромбом называется параллелограмм, у которого все стороны равны. Если у ромба все углы прямые, тогда он называется квадратом.
Свойства ромба
- Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
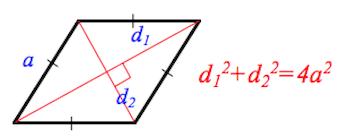
- Диагонали перпендикулярны.
- Диагонали являются биссектрисами его углов.
- Центром вписанной в ромб окружности будет точка пересечения его диагоналей.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.
- Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.
Формулы определения длины стороны ромба:
(a=frac{S}{h_a}; a=sqrt{frac{S}{sinalpha}}; a=frac{S}{2r}; a=frac{sqrt{d_1^2+d_2^2}}{2}).
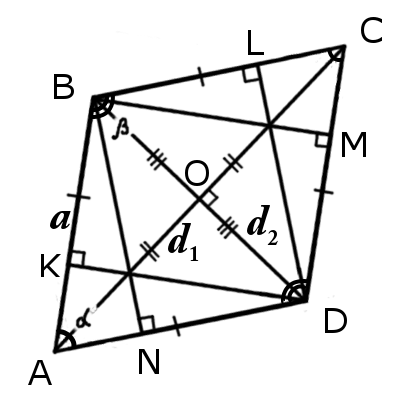
Формулы определения длины диагонали ромба:
(d_1=asqrt{2-2cosbeta}; d_2=asqrt{2+2cosbeta}; d_1=sqrt{4a^2-d_2^2}; d_2=sqrt{4a^2-d_1^2}).
Диагональ ромба равна его стороне. Найдите меньший угол ромба.
В параллелограмме (ABCD) сторона (AB=7, AD=3,sinA=frac67). Найдите большую высоту параллелограмма.
Биссектриса одного из углов прямоугольника делит сторону прямоугольника пополам. Найдите периметр прямоугольника, если его меньшая сторона равна 10.
Диагональ квадрата равна (2sqrt{8}) см. Найдите сторону квадрата.
Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Числовое значение площади прямоугольника принадлежит промежутку
Источник
Видеоурок 1: Прямоугольник, ромб и квадрат. Часть 1
Видеоурок 2: Прямоугольник, ромб и квадрат. Часть 2
Лекция: Параллелограмм, прямоугольник, ромб, квадрат
 Четырехугольники
Четырехугольники
Один подраздел многоугольников мы изучили в прошлом вопросе, сейчас же перейдем к изучению четырехугольников – это многоугольники, у которых 4 стороны, 4 вершины, 4 угла.
В школьном курсе геометрии изучают несколько основных типов четырехугольников – это параллелограмм, прямоугольник, ромб, квадрат и трапецию. В этом же вопросы мы рассмотрим все, кроме трапеции, поскольку все первые 4 типа многоугольников имеют некоторые похожие черты – у них противолежащая пара сторон параллельна.
Отличительная особенность всех четырехугольников – это то, что сумма всех углом равна 360 градусов.
Ну давайте начнем характеризовать все четырехугольники, имеющиеся в теме.
 Параллелограмм
Параллелограмм
Исходя из названия, можно судить, что у данного четырехугольника что-то параллельное. Это совершенно верно, параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

Все четырехугольники характеризуются своими свойствами, поэтому давайте ознакомимся со свойствами параллелограмма:
Параллельные стороны параллелограмма попарно равны между собой

Противолежащие углы параллелограмма также равны

Диагонали параллелограмма пересекаются в точке, которая делит из пополам

Если у четырехугольника присутствуют перечисленные свойства, то он является параллелограммом:
- Какой – то Один признак выполнен
- Все свойства параллелограмма можно использовать
Для любого параллелограмма справедлива следующая формула, по которой ясно, что сумма квадратов сторон диагоналей равна сумме квадратов всех сторон:

Данное свойство вытекает из теоремы Пифагора для двух прямоугольных треугольников.
Любую сторону можно найти по известным величинам диагоналей и углов между ними:

Найти стороны параллелограмма можно не только через диагонали, но и через высоты и площади:

Одними из наиболее важных формул являются формулы для нахождения диагоналей найти их можно по известным сторонам и углу между ними:

Но на самом деле самыми важными формулами являются формулы для нахождения площадей:

 Квадрат
Квадрат
Правильный четырехугольник – это квадрат. Как известно, у всех правильных фигур равны стороны и равны углы. Квадрат можно назвать частным случаем параллелограмма, поскольку все свойства и признаки параллелограмма видны и у квадрата.Свойства квадрата:
- Все стороны равны.
- Все углы равны 90 градусам.
- Диагонали квадрата равны и пересекаются под прямым углом, а точка их пересечения делит их пополам.

Отличительной особенностью диагонали квадрата является то, что она есть гипотенузой прямоугольного треугольника с катетами, равными сторонам квадрата, а гипотенузой равной диагонали. Именно поэтому из теоремы Пифагора диагональ квадрата всегда в раз больше его стороны.

Так как у квадрата все стороны равны, то найти периметр и площадь этой фигуры не составляет ни малейшего труда:


 Прямоугольник
Прямоугольник
Эта фигура характеризуется тем, что все её углы прямые, то есть по 90 градусов.
Свойства прямоугольника:
У прямоугольника все противолежащие стороны параллельны и равны между собой.
Все углы прямые.
Точка пересечения диагоналей делит их на равные части.

Квадрат диагонали прямоугольника равен сумме квадратов его сторон:

Как можно было понять, данная формула была выведена из теоремы Пифагора, поскольку в основе прямоугольника лежат 2 прямоугольных треугольника.
Формулы нахождения сторон по известным величинам диагоналей, а также площадей:
Формулы сторон прямоугольника

Формулы периметра прямоугольника

Формулы площадей

 Ромб
Ромб
И наконец-то мы подошли к последнему из параллелограммов, который называется ромбом.
У ромба, как и у квадрата, все стороны равно, но, как и у любого параллелограмма, его стороны попарно параллельны.
Отличительной особенностью ромба считается то, что его диагонали, пересекаясь под прямым углом, делятся пополам.
Не имеет смысла перечислять все свойства ромба, поскольку они аналогичны свойствам параллелограмма, а так же квадрата.
У ромба так же существует связь между длинами диагоналей и его сторон. Поскольку в основании ромба лежат 4 прямоугольных треугольника, то можно было вывести формулу связи диагоналей и сторон через теорему Пифагора:

Формулы для сторон ромба

Формулы площадей ромба

Источник

