Что такое ромб квадрат какие их свойства

Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
Источник:
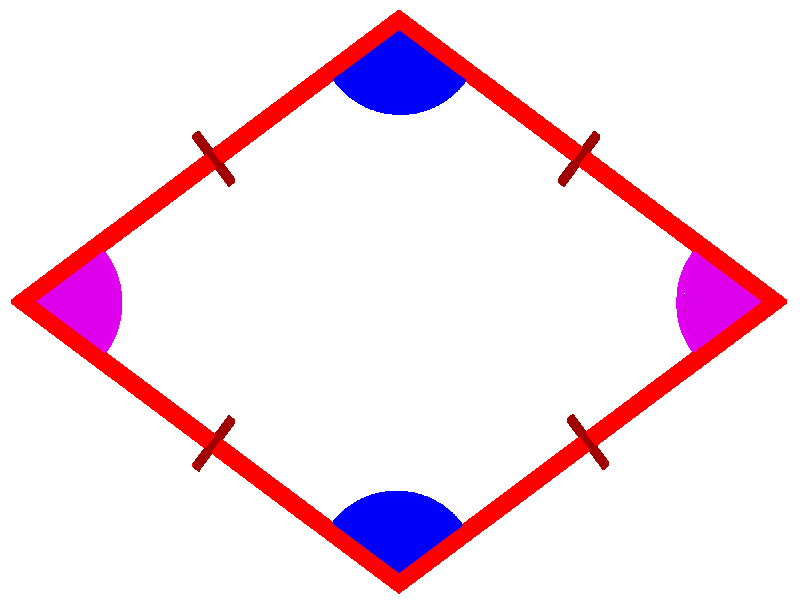
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
Источник:
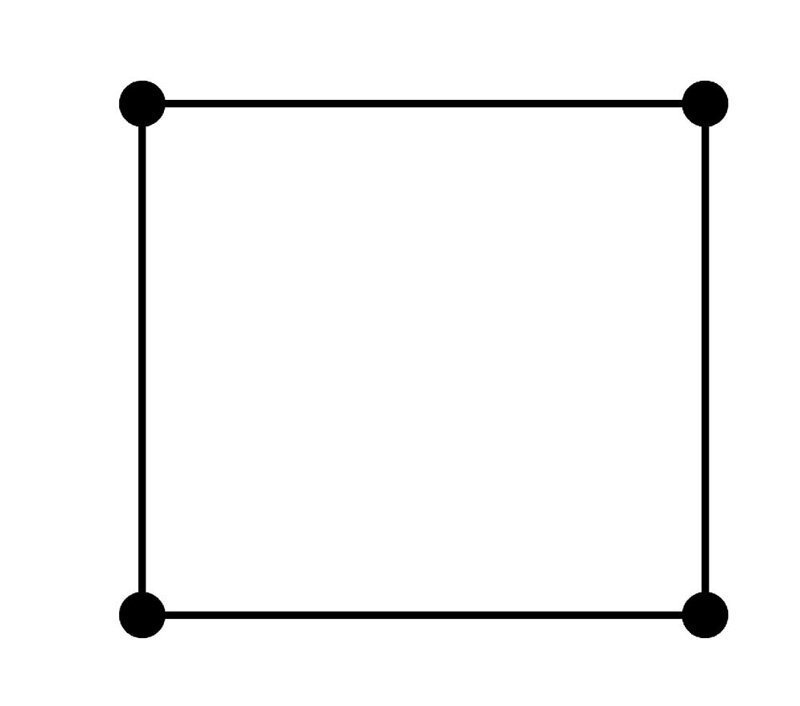
С квадратом все намного проще, его определение звучит так: квадрат – это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:

Понравился пост? Поддержи Фишки, нажми:
Источник
Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма.
Определение 2
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой.
Напомним основные свойства параллелограмма.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Рассмотрим далее подробно понятия прямоугольника, ромба и квадрата.
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
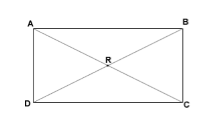
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $angle B=angle A={90}^0$, а $AB$ – общая сторона, то по I признаку равенства треугольников, $triangle ABD=triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $angle DRC=angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $triangle DRC=triangle ARB$. Значит, $angle RDC=angle RCD=angle RAB={rm }angle RBA$.
Так как $angle DRA=angle CRB$, как вертикальные, то по I признаку равенства треугольников $triangle DRA=triangle CRB$. Значит, $angle RDA=angle RAD=angle RCB={rm }angle RBC$.
Следовательно, $angle A=angle B=angle C=angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
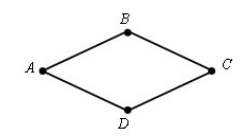
Рисунок 3. Ромб
Рассмотрим свойство ромба.
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).
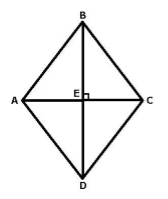
Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ – медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).

Рисунок 5. Квадрат
Очевидно, что квадрат — частный случай ромба. Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.
Пример задачи
Пример 1
Найти периметр квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
[a^2+a^2=100] [{2a}^2=100] [a^2=50] [a=5sqrt{2}] [P=4a=20sqrt{2}]
Ответ: $20sqrt{2}$.
Источник
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Источник
Комментарии преподавателя
Ромб и квадрат
1. Ромб и его свойства
Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма. Однако есть и специфические свойства, о которых пойдёт речь. Но для начала сформулируем одно из определений ромба.
Ромб – это параллелограмм, у которого все стороны равны.
Сформулируем и докажем теорему о свойствах ромба.
Теорема
Диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов) (см. Рис. 1).
Дано:
– ромб
Доказать:
.
Доказательство:
Рис. 1
Рассмотрим : – середина (так как ромб является параллелограммом, то его диагонали в точке пересечения делятся пополам). Кроме того, из определения ромба следует, что . Значит, треугольник – равнобедренный; является медианой этого треугольника, проведённой к основанию, а, значит, и биссектрисой, и высотой. Из этого следует, что:
, то есть диагонали ромба перпендикулярны;
, то есть диагонали ромба являются биссектрисами его углов (равенство остальных углов можно доказать аналогично).
Доказано.
Ещё один частный случай параллелограмма – квадрат.
2. Квадрат и его свойства
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат обладает всеми свойствами прямоугольника и ромба. А именно:
· все углы квадрата прямые;
· диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делят углы квадрата пополам.
3. Задачи на ромб и квадрат
Теперь рассмотрим несколько задач, в которых встречаются ромб и квадрат.
Задача 1.
В ромбе одна из диагоналей равна стороне (см. Рис. 2). Найти:
а) углы ромба;
б) углы между диагоналями и сторонами.
Дано: – ромб; .
Найти: а) ; б) .
Решение:
Рис. 2
а) (так как у ромба все стороны равны). Значит, треугольник – равносторонний. Отсюда следует, что угол . Так как в любом параллелограмме сумма соседних углов равна , то .
Ответ: .
б) По доказанной выше теореме: . Аналогично получаем, что .
Ответ: .
Задача 2.
Найти периметр ромба , в котором , а меньшая диагональ равна . Найти периметр ромба.
Дано: – ромб; .
Найти:
Решение:
Рис. 3
Рассмотрим треугольник , в нём: . Значит, данный треугольник равнобедренный, угол при вершине у него равен , два других угла при основании равны, поэтому данный треугольник – равносторонний. Значит: . Так как в ромбе все стороны равны, то периметр ромба равен: .
Ответ: .
Задача 3.
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .
Дано: – ромб, .
Найти:
Решение:
Рис. 4
Вспомним, что в любом параллелограмме противоположные углы, а сумма углов, прилежащих к одной стороне, равна . Из этого следует, что: . Теперь воспользуемся доказанной вначале теоремой: .
Ответ:
Задача 4.
Докажите, что параллелограмм является ромбом, если:
а) его диагонали взаимно перпендикулярны;
б) его диагонали являются биссектрисами углов.
а) Дано: – параллелограмм, .
Доказать: – ромб.
Доказательство:
Рис. 5
Рассмотрим треугольник : в нем является одновременно и высотой (так как диагонали перпендикулярны), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть – ромб.
Доказано.
б) Дано: – параллелограмм, – биссектрисы углов параллелограмма.
Доказать: – ромб.
Доказательство:
Рис. 6
Рассмотрим треугольник : в нем является одновременно и биссектрисой (так как диагонали являются биссектрисами углов), и медианой (так как диагонали в любом параллелограмме точкой пересечения делятся пополам). Значит, – равнобедренный. Из этого следует, что: . Если теперь воспользоваться тем, что в параллелограмме противоположные стороны равны, получаем, что: . То есть, – ромб.
Доказано.
Задача 5.
Докажите, что ромб, у которого один из углов прямой, является квадратом.
Дано: – ромб,
Доказать: – квадрат.
Доказательство:
Рис. 7
Вспомним, что квадрат – это одновременно прямоугольник и ромб. Если говорить о сформулированном строгом определении, то квадрат – это прямоугольник, у которого все стороны равны. Равенство сторон следует из того, что данный четырёхугольник – ромб. Осталось доказать, что он является ещё и прямоугольником. По условию: (у любого параллелограмма противоположные углы равны). Кроме того, сумма соседних углов параллелограмма равна . Значит: . Отсюда мы получаем, что – прямоугольник, а значит, и квадрат.
Доказано.
На этом уроке мы изучили ромб и квадрат, а также рассмотрели их свойства и решили различные задачи, в которых встречаются ромб и квадрат.
ИСТОЧНИК
https://x-uni.com/geometriya/8-klass/video/romb-i-kvadrat
https://www.youtube.com/watch?v=axMe7L_01j0
https://www.youtube.com/watch?v=y4x7r57AuSM
https://fs1.ppt4web.ru/uploads/ppt/17412/2387c05b0d646493088efdb6da84d39d.ppt
https://prezentacii.com/uploads/ppt/03-13/Prjamougolnik-Romb-Kvadrat.rar
https://900igr.net/prezentatsii/geometrija/Prjamougolnik-romb-kvadrat/Prjamougolnik-romb-kvadrat.html
https://u.900igr.net/zip/397eb071b35912c86e9059e79cf8ca54.zip
https://player.myshared.ru/1246878/data/images/img3.jpg
https://www.euroki.net/books/gdzs/273/112569.png
https://900igr.net/datas/geometrija/Prjamougolnik-romb-kvadrat/0005-005-Otvety-k-proverochnomu-testu.jpg
Источник
Квадрат это всегда ромб? Ромб и квадрат – это одно и то же? Почему квадрат это ромб? Эл Лепсоид более года назад Всё, как известно, познаётся в сравнении. Для ответа на поставленные вопросы (а их, с учетом пояснений, несколько) посмотрим, какие определения даются указанным геометрическим фигурам. Вот, например, ромбом называется Хотя есть и более обобщенное определение, согласно которому ромб – это Теперь смотрим на квадрат и видим, что им называют Но в более общем варианте квадрат – это Если сравнивать обобщенные варианты определения указанных фигур, то видим, что разница между ними только в дополнительной характеристике квадрата – у него все углы между собой равны. Так что, отвечая на основной вопрос можно сказать, что квадрат является ромбом, у которого все углы равны. И он всегда будет ромбом, как его не крути-верти. Получается, что квадрат – это разновидность ромба с одинаковыми углами. А вот сказать, что квадрат и ромб есть одно и то же, вряд ли получится, т.к., если квадрат можно считать разновидностью ромба (см. выше), то уж ромб в общем случае квадратом не является – так полной идентичности между ними нет. автор вопроса выбрал этот ответ лучшим Lolytushka более года назад Квадрат и ромб – это геометрические фигуры, которые имеют сходство по некоторым признакам. Главное отличие между ними состоит в том, что у квадрата обязательно все углы равны и являются прямыми, а у ромба равны только противоположные углы. То есть ромб не является квадратом, а вот квадрат вполне можно считать ромбом, одной из его разновидностей, так как все признаки есть для этого. Обе эти фигуры являются параллелограммами (противоположные стороны у них параллельны), имеют равенство всех сторон, а также их диагонали перпендикулярны друг другу. Рысси более года назад Квадрат и ромб это четырехугольники со схожими признаками, и у одного и у другого все стороны равны, в отличие от ромба у квадрата есть еще равность углов 90 градусов, у ромба углы разные, отсюда сделаем вывод что квадрат частный случай ромба, но никак не наоборот. Если поставить квадрат на один из углов он будет выглядеть как тот же ромб. Смотрим и удивляемся. ЛАТЫШКА более года назад Ещё как является! Безусловна одинаковость – равные стороны, он и параллелограммом является, если углубляться дальше: параллельность сторон. Потому с полным правом можно называть квадрат и ромбом, у которого все углы равны. Квадрат и ромб – разные геометрические фигуры, но квадрат это всегда и ромб, одновременно. Ответ : квадрат всегда является и ромбом андреюшка более года назад Квадрат можно считать только разновидностью ромба, но не самим ромбом. Ромб и квадрат – это принципиально разные фигуры. А быть разновидностью друг друга могут быть. С таким же успехом можно сказать, что и ромб является квадратом, ведь у него все стороны равны! Но правильнее начинать с того, что, по классике, квадрат является разновидностью прямоугольника, а ромб является разновидностью параллелограмма. Вот это будет самое правильное. Так и учат детей в школе. Прямоугольник, кстати, тоже является разновидностью параллелограмма. То есть у параллелограмма есть два класса, различаемые по разным признаками – по сторонам и по углам. Если все стороны равны, то этот параллелограмм – ромб. А если все углы прямые – то этот параллелограмм – прямоугольник. А разновидность прямоугольника – квадрат. И не надо дальше мешать между собой два этих признака. То что вы считаете квадрат ромбом – это никому не нужно (хотя это так), и никакой пользы не несет. Это все равно что взять такое общее понятие как одежда. У одежды есть две классификации – это штаны и рубашки. Это совершенно разные виды одежды. Но теперь добавим комбинезон. Что такое комбинезон? Можно сказать, что это рубашка, к которой пришиты штаны. А можно сказать, что это штаны, к которой пришита рубашка. То есть комбинезон, получается, это и штаны, и рубашка одновременно. Хотя, по сути, комбинезон, это новый вид одежды. Здесь как и в случае с ромбом/квадратом имеют место лишние заумствования, которые никому не нужны. Поэтому следует считать квадрат прямоугольником и не лезть в ромбовидное “царство”. Для квадрата главное – углы по 90 градусов. А для ромба главное, что у него все стороны равны, при этом лучше всего считать, что у него углы не 90 градусов. BAU более года назад Да, квадрат это всегда ромб. Ромб это не всегда квадрат. Квадрат просто частный случай ромба у которого прямые углы, а не только равные стороны. Безразличный более года назад Ромб обычно изображают несколько иначе. Квадрат рисуют лежащем на одном из оснований. А ромб изображают одной из вершин угла вниз. Поверните квадрат на 45 градусов и получите типичный ромб. Ромб это фигура, у которой все стороны раны. Квадрат тоже с такими же равными сторонами. Отсюда: квадрат, один из частных случаев ромба. Или так: квадрат это ромб с равными углами. Бекки Шарп более года назад Квадрат и ромб – плоские геометрические фигуры. И тот и тот имеют четыре стороны и четыре угла. И У ромба и у квадрата стороны равны. У квадрата еще и равны все углы, в отличие от ромба. Определение ромба же – это параллелограмм, у которого все стороны равны. Под это условие подходит и квадрат тоже. Квадрат – это ромб. Росинка Роса более года назад Квадрат это всегда ромб. Одно из его проявлений Ромб и квадрат – это не одно и то же. При одном и том же признаке – равенство сторон, у ромба углы могут быть попарно равны , и отличаться от 90 градусов. В квадрате же все стороны равны, и все углы равны – по 90 градусов Квадрат это частный случай ромба. Мозгунова Ирина более года назад Да, квадрат – это всегда ромб. Только у этого ромба все углы прямые. От четырёхугольника – к квадрату. Среди множества четырёхугольников существуют такие, у которых противоположные стороны параллельны – это параллелограммы. Среди множества параллелограммов есть фигуры, у которых все стороны равны – это ромбы. Среди множества ромбов есть такие, у которых все углы прямые – это квадраты. СТЭЛС более года назад Квадрат вполне отвечает требованиям предъявляемым к ромбу как к геометрической фигуре – квадрат параллелограмм? – да!, у квадрата все стороны равны? – да! Значит есть все формальные основания считать квадрат ромбом. Знаете ответ? |
Источник



