Что такое средняя линия треугольника какие ее свойства
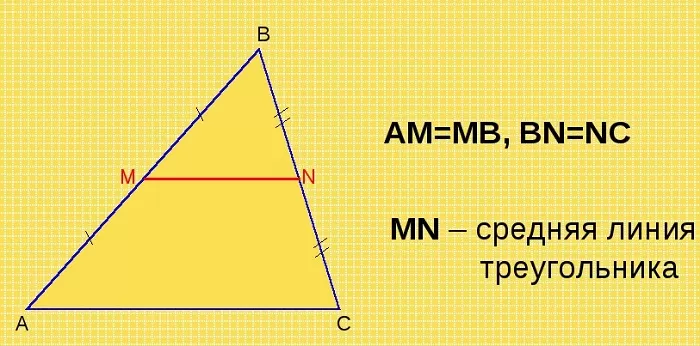
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
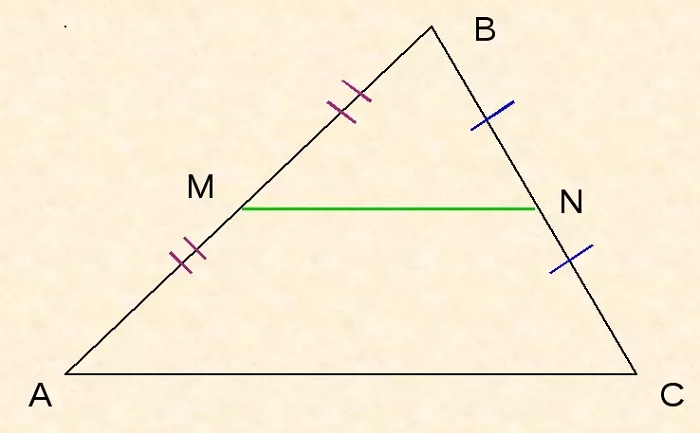
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
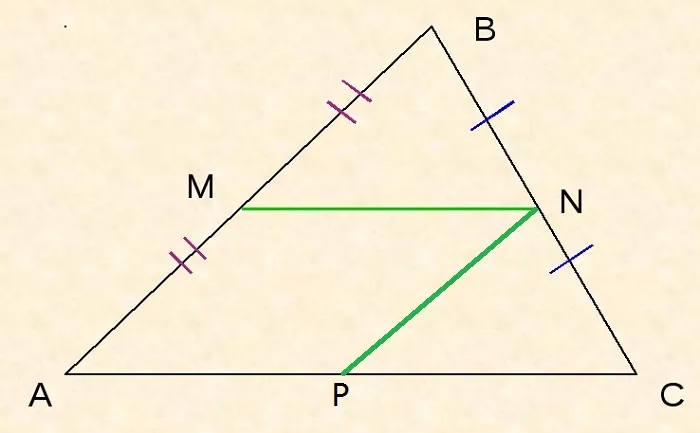
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
![]()
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
![]()
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
![]()
Поскольку в результате образуется замкнутая ломаная, то
![]()
Отсюда следует, что
![]()
Так как
![]()
то
![]()
![]()
Из последнего равенства следуют условия теоремы.
Доказано.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.

По определению стороны AB и BC делятся пополам, поэтому
![]()
Согласно теореме,
![]()
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
![]()
Доказано.
Следствие №2
Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.
Доказательство.
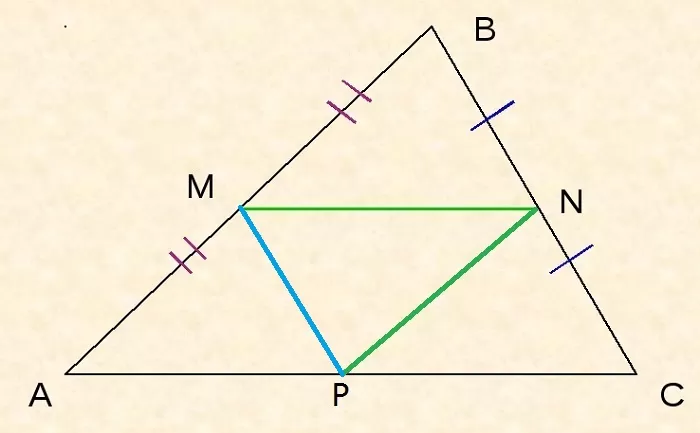
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
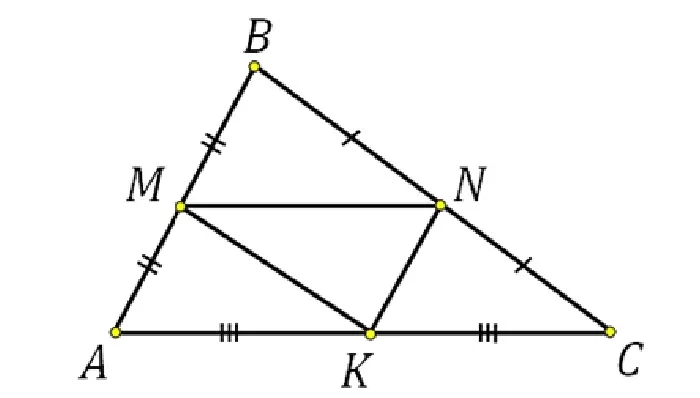
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
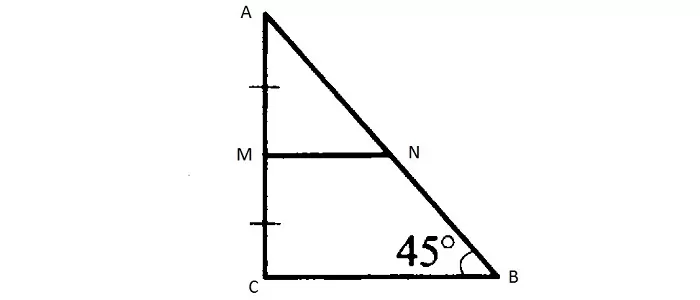
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
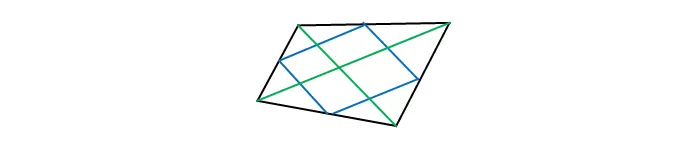
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Решение.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Доказано.
Источник
[{Large{text{Подобие треугольников}}}]
Определения
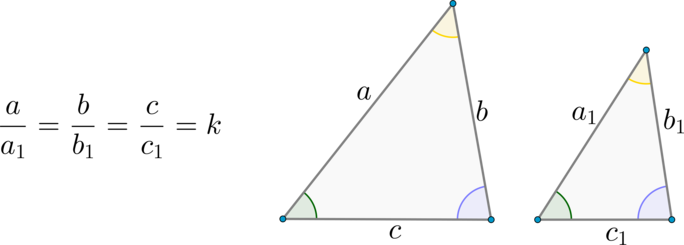
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники (ABC) и (A_1B_1C_1) со сторонами (a,b,c) и (a_1, b_1, c_1) соответственно (см. рисунок выше).
Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1})
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники (ABC) и (A_1B_1C_1) подобны, причём (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = dfrac{BC}{B_1C_1} = k). Обозначим буквами (S) и (S_1) площади этих треугольников соответственно.
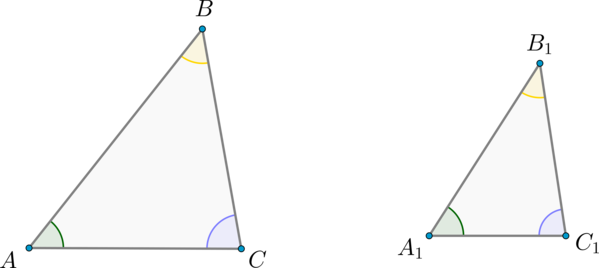
Так как (angle A = angle A_1), то (dfrac{S}{S_1} = dfrac{ABcdot
AC}{A_1B_1cdot A_1C_1}) (по теореме об отношении площадей треугольников, имеющих по равному углу).
Так как (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = k), то (dfrac{S}{S_1} = dfrac{AB}{A_1B_1}cdotdfrac{AC}{A_1C_1} = kcdot k = k^2), что и требовалось доказать.
[{Large{text{Признаки подобия треугольников}}}]
Теорема (первый признак подобия треугольников)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть (ABC) и (A_1B_1C_1) – треугольники такие, что (angle A =
angle A_1), (angle B = angle B_1). Тогда по теореме о сумме углов треугольника (angle C = 180^circ – angle A – angle B = 180^circ
– angle A_1 – angle B_1 = angle C_1), то есть углы треугольника (ABC) соответственно равны углам треугольника (A_1B_1C_1).
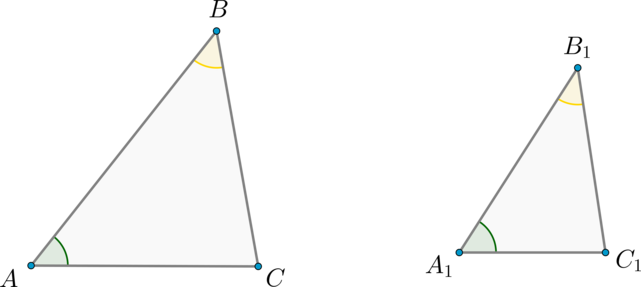
Так как (angle A = angle A_1) и (angle B = angle B_1), то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1}) и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1}).
Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1}).
Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1}) (используя равенства (angle B = angle B_1), (angle C = angle C_1)).
В итоге, стороны треугольника (ABC) пропорциональны сходственным сторонам треугольника (A_1B_1C_1), что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника (ABC) и (A’B’C’), таких что (dfrac{AB}{A’B’}=dfrac{AC}{A’C’}), (angle BAC = angle A’). Докажем, что треугольники (ABC) и (A’B’C’) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B’).
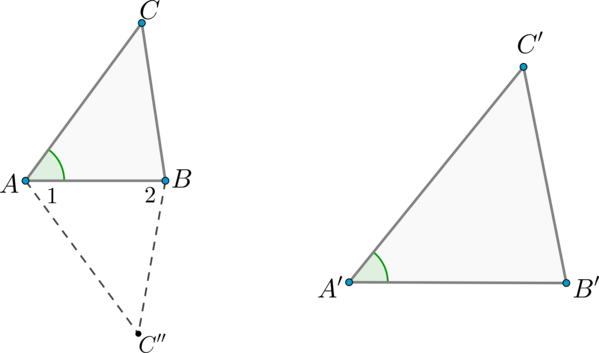
Рассмотрим треугольник (ABC”), у которого (angle 1 = angle A’), (angle 2 = angle B’). Треугольники (ABC”) и (A’B’C’) подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A’B’} =
dfrac{AC”}{A’C’}).
С другой стороны, по условию (dfrac{AB}{A’B’} = dfrac{AC}{A’C’}). Из последних двух равенств следует, что (AC = AC”).
Треугольники (ABC) и (ABC”) равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B’).
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников (ABC) и (A’B’C’) пропорциональны: (dfrac{AB}{A’B’} = dfrac{AC}{A’C’} = dfrac{BC}{B’C’}). Докажем, что треугольники (ABC) и (A’B’C’) подобны.
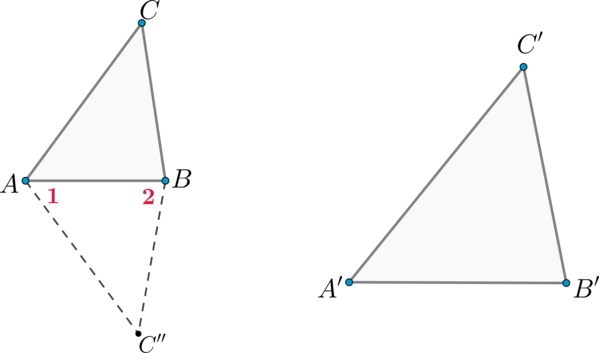
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A’).
Рассмотрим треугольник (ABC”), у которого (angle 1 = angle A’), (angle 2 = angle B’).
Треугольники (ABC”) и (A’B’C’) подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A’B’} = dfrac{BC”}{B’C’}
= dfrac{C”A}{C’A’}).
Из последней цепочки равенств и условия (dfrac{AB}{A’B’} =
dfrac{AC}{A’C’} = dfrac{BC}{B’C’}) вытекает, что (BC = BC”), (CA
=
C”A).
Треугольники (ABC) и (ABC”) равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A’).

[{Large{text{Теорема Фалеса}}}]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму: Если в (triangle OBB_1) через середину (A) стороны (OB) проведена прямая (aparallel BB_1), то она пересечет сторону (OB_1) также в середине.
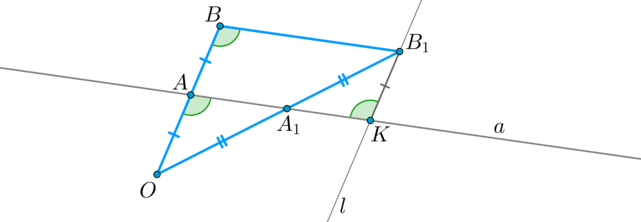
Через точку (B_1) проведем (lparallel OB). Пусть (lcap a=K). Тогда (ABB_1K) — параллелограмм, следовательно, (B_1K=AB=OA) и (angle
A_1KB_1=angle ABB_1=angle OAA_1); (angle AA_1O=angle KA_1B_1) как вертикальные. Значит, по второму признаку (triangle
OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1). Лемма доказана.
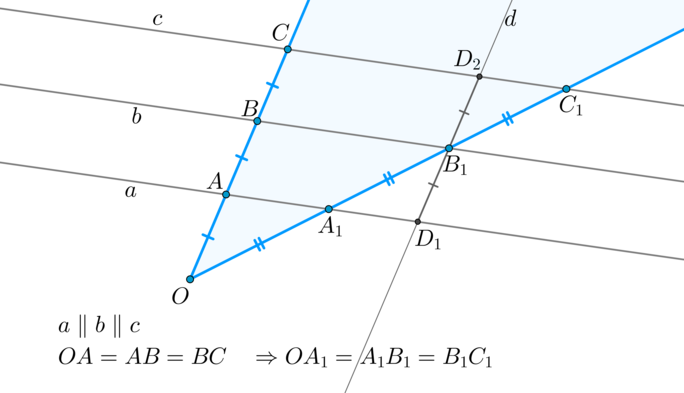
Перейдем к доказательству теоремы. Пусть (OA=AB=BC), (aparallel
bparallel c) и нужно доказать, что (OA_1=A_1B_1=B_1C_1).
Таким образом, по данной лемме (OA_1=A_1B_1). Докажем, что (A_1B_1=B_1C_1). Проведем через точку (B_1) прямую (dparallel OC), причем пусть (dcap a=D_1, dcap c=D_2). Тогда (ABB_1D_1, BCD_2B_1) — параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2). Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2) как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1) как накрест лежащие, и, значит, по второму признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1).
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
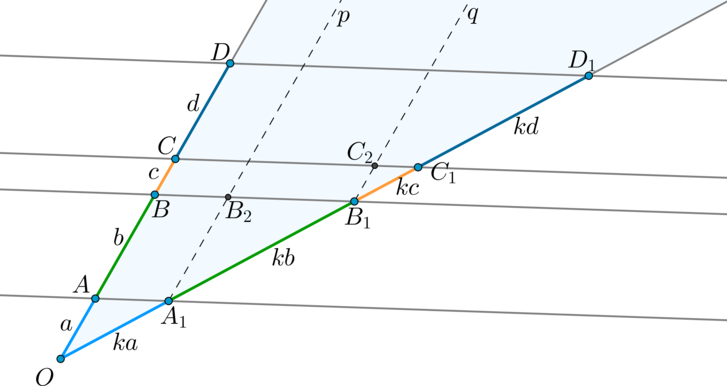
Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s) разбили одну из прямых на отрезки (a, b, c, d). Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd) соответственно, где (k) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1) прямую (pparallel OD) ((ABB_2A_1) — параллелограмм, следовательно, (AB=A_1B_2)). Тогда (triangle OAA_1
sim triangle A_1B_1B_2) по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb).
Аналогично проведем через (B_1) прямую (qparallel OD Rightarrow
triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc) и т.д.

[{Large{text{Средняя линия треугольника}}}]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы.
2) Докажем, что (MN=dfrac12 AC).
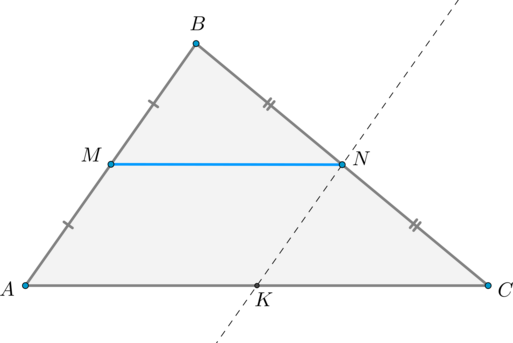
Через точку (N) проведем прямую параллельно (AB). Пусть эта прямая пересекла сторону (AC) в точке (K). Тогда (AMNK) — параллелограмм ((AMparallel NK, MNparallel AK) по предыдущему пункту). Значит, (MN=AK).
Т.к. (NKparallel AB) и (N) – середина (BC), то по теореме Фалеса (K) – середина (AC). Следовательно, (MN=AK=KC=dfrac12 AC).
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12).
Источник
1) Средняя линия параллельна третьей стороне треугольника и равна ее половине;
2) Средняя лини отсекает треугольник, подобный исходному, с коэффициентом подобия .
Сумма внутренних углов треугольника
Сумма внутренних углов треугольника равна 180º.
Прямоугольный треугольник
1) Теорема Пифагора:В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов: c2=a2+b2, где гипотенуза AB=c, катеты AC=b,
BC= a.
2) Теорема, обратная теореме Пифагора: Если в некотором треугольнике квадрат длины одной стороны равен сумме квадратов длин двух других сторон, то этот треугольник – прямоугольный.
3) В прямоугольном треугольнике выполняются следующие соотношения между его сторонами и углами (рис.6.5): , , , . Эти соотношения также принято называть «решениями прямоугольного треугольника».
4) Проекции c1,c2 соответственно катетов a, bна гипотенузу обладают следующими свойствами (рис. 6.6): , , ,
5) Медиана, проведенная из вершины прямого угла на гипотенузу, равна половине гипотенузы: . Верно также и обратное утверждение: если в некотором треугольнике длина одной из медиан равна половине той стороны, которую она делит пополам, то этот треугольник является прямоугольным (рис. 6.7).
Четырехугольники
Параллелограмм и его свойства
1) Противоположные стороны параллелограмма равны;
2) Противоположные углы параллелограмма равны;
3) Сумма углов, прилежащих к любой из сторон параллелограмма, равна 180º;
4) Диагонали параллелограмма делятся точкой их пересечения пополам;
5) Точка пересечения диагоналей параллелограмма является его центром симметрии;
6) Сумма квадратов длин диагоналей параллелограмма равна удвоенной сумме квадратов длин его сторон: d21 + d22 = 2(a2 + b2) (рис. 6.8).
Ромб и его свойства
1) Все стороны ромба равны;
2) Диагонали ромба взаимно перпендикулярны и являются биссектрисами его внутренних углов;
3) Прямые, содержащие диагонали ромба, являются его осями симметрии (рис. 6.9).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Дан правильный треугольник ABC. На продолжении стороны АС за точку С взята точка D, а на продолжении стороны ВС за точку С – точка Е так, что BD=DE. Докажите, что AD=CE.
Решение.
На отрезке CE отметим точку F такую, что FE=BC (см. рис.). Треугольники BDC и EDF равны по первому признаку равенства треугольников. Отсюда CD=DF. Далее, поскольку DFC= DCF= ACB=60°, треугольник CDF – равносторонний. Поэтому CF=CD и AD=AC+CD=BC+CF=FE+CF=CE, что и требовалось доказать.
2.Медианой пятиугольника ABCDE назовем отрезок, соединяющий вершину с серединой противолежащей стороны (А – с серединой CD, В – с серединой DE и т.д.). Докажите, что если четыре медианы выпуклого пятиугольника перпендикулярны сторонам, к которым они проведены, то таким же свойством обладает и пятая медиана.
Решение.Условие перпендикулярности медианы пятиугольника и его противолежащей стороны равносильно тому, что диагонали, проведенные из соответствующей вершины, равны. Поэтому, если медианы, проведенные из вершин A, B, C и D, перпендикулярны противолежащим сторонам, то выполняются равенства AC=AD, BE=BD, CA=CE, DB=DA. Отсюда следует, что CE=BE, т.е. медиана, проведенная из вершины E, также перпендикулярна противолежащей стороне.
3.На сторонах AB и BC треугольника ABC построены внешним образом квадраты ABDE и BCPG . Оказалось, что прямая DG параллельна прямой AC . Докажите, что треугольник ABC — равнобедренный.
Решение.Треугольники ABG и DBC равны (AB =DB, BG = BC, углы ABG и DBC равны). Значит, AG=CD, и четырехугольник ADGC – трапеция с равными диагоналями. Но такая трапеция является равнобедренной: AD=CG. Но если диагонали квадратов равны, то равны и их стороны: AB=BC.
4.Разделите данный отрезок АВ на четыре равные части с помощью циркуля и линейки, проведя всего 6 линий (прямых и окружностей).
Решение. Проведем две окружности радиуса АВ с центрами в точках А и В. Через точки пересечения этих окружностей проведем прямую, которая пересекает отрезок АВ в точке С. Проведем теперь окружность с центром в точке С радиусом АВ. Эта окружность пересечет каждую из проведенных окружностей в двух точках. И, наконец, проведем через эти две пары точек две прямые — см. рис. 11. Таким образом, мы провели 6 линий: три окружности и три прямые. Докажем, что три проведенные прямые делят отрезок А В па четыре равные части. Как известно, геометрическим местом точек, равноудаленных от концов отрезка, является серединный перпендикуляр этого отрезка — прямая, проведенная через середину данного отрезка перпендикулярно к нему. Две точки пересечения двух первых построенных окружностей находятся на одинаковом расстоянии АВ от точек А и В, поэтому прямая, проходящая через них, является серединным перпендикуляром отрезка АВ и делит его на две равные части в точке С.
Аналогично точки пересечения третьей окружности с одной из первых двух находятся на одинаковом расстоянии А В и от середины С отрезка АВ, от конца. Аналогично точки пересечения третьей окружности с одной из первых двух находятся на одинаковом расстоянии А В и от середины С отрезка АВ, и от конца этого отрезка, поэтому прямая, проходящая через эти
точки пересечения, делит половину отрезка АВ еще раз пополам.
5.Дан равнобедренный треугольник с углом 20° при вершине. Докажите, что его боковая сторона больше удвоенного основания.
Решение. Пусть ABC — данный треугольник, AB = AC, CAB = 20°. Отложим на стороне АВ отрезок BE, равный отрезку ВС (см. рис.). Тогда CEB = ECB = 50°, ACE = 30°, а так как в треугольнике против большего угла лежит большая сторона, то АЕ > СЕ и СЕ > СВ. Следовательно, АВ = АЕ + ВЕ> 2СВ.
6.Отрезки АС и ВD пересекаются в точке О. Известно, что равны периметры треугольников АВС и АВD, а также равны периметры треугольников АСD и ВСD. Найдите длину АО, если ВО=10 см.
Решение: Из равенства периметров треугольников получаем, что
АС + ВС = АD + ВD и АD+АС=ВD+ВС.
Вычитая из первого равенства второе, получим, что ВС=АD, а тогда АС=ВD. Из равенства треугольников АВD и АВС получаем равенство углов АВD и ВАС. А тогда треугольник АОВ равнобедренный и АО=ВО=10 см.
7.На гипотенузе BCпрямоугольного треугольника ABC выбрана точка Kтак, что AB = AK. Отрезок AK пересекает биссектрису CL в ее середине. Найдите острые углы треугольника ABC.
Ответ.
Решение. Обозначим середину биссектрисы CLчерез P, а угол ABCчерезb; тогда . В прямоугольном треугольнике ACLотрезок AP является медианой, поэтому AP = CP = LP. Теперь из равнобедренных треугольников APLи ABKполучаем . С другой стороны, как внешний угол в . Значит, , откуда , или . Тогда .
8.Три стороны трапеции равны по 10 дм, а острый угол равен 60°. Найти длину отрезка, соединяющего центр вписанной окружности с вершиной меньшего основания.
Решение. Пусть в трапеции KNML (NM || KL) KN = NM = ML = 10 дм, . Заметим, что и, так как , то . Значит . Так как ON = OM– как радиусы, то – равнобедренный, т.е. , но тогда . Выходит, что – равносторонний и MO = MN = 10 дм.
9.В параллелограмме АСВМ АС = 16 м, СВ = 24 м, СЕ и CF — соответственно высоты, проведенные к сторонам AM и ВМ, ÐECF = 60°. Найти длину высоты СЕ.
Решение.
По условию в параллелограмме ACBMCE^AMи ÐECF =60º, тогда ÐACE =30º. Значит, AE=1/2 · AC = 8 (м).
Из Δ AEC, где AC=16 м, AE=8 м, CE2=AC2-AE2, или (м).
10.По трем медианам ma, mb и mc ΔАВС, найти длину стороны AC=b.
Решение. Так как точка O – точка пересечения медиан, то , , .
Достроим Δ AOCдо параллелограмма AOCE. Известно, что в параллелограмме AC2 +OE2 = 2(AO2 + OC2), или , откуда находим .
11.Найти длину средней линии прямоугольной трапеции, вписанной в окружность, если расстояния от центра окружности до концов большей боковой стороны равны соответственно 6 и 8 дм.
Решение. Поскольку O – центр вписанной окружности, то MOи NO – биссектрисы углов KNMи LMN, тогда , т.е. ÐMON=90º, тогда, из ΔMON (дм).
Заметим, что высота OAΔOMNявляется одновременно и радиусом вписанной окружности, тогда , откуда OA = 4,8 (дм2). Значит, KL=2·OA=9,6 (дм). По свойству описанного четырехугольника KN + LM=KL + MN=10+9,6=19,6 (дм), тогда (дм).
12.Сумма числа сторон выпуклого многоугольника и числа его диагоналей равна 21. Определить число сторон многоугольника.
Решение. Пусть x число сторон(а значит и вершин) многоугольника. Заметим, что из каждой вершины многоугольника можно провести (x– 3) диагонали, а из всех его вершин – в x раз больше. Тогда общее число диагоналей многоугольника будет равно . Согласно условию, имеем уравнение: . Решая его, найдем, что x=7.
13.Внутри угла в 60° дана точка М, удаленная от сторон угла на 2 и 11 единиц. Найти расстояние точки М от вершины угла.
Решение. Пусть AM = 2, MB = 11. Продолжим AM до пересечения в точке D со стороной DO данного угла. Δ OAD и ΔMBD – прямоугольные с общим углом ADOв 30º.
ИзΔOAMи Δ OAD, MD = 2MB = 22, AD = AM + MD = 24; OD = 2 · OA, OM = 14.
14.Диагональ параллелограмма делит его угол в отношении 1:3. Найти углы параллелограмма, если длины сторон относятся как 1:2.
Решение.
ПустьAB = x, BC = 2x, ÐCBD = a, ÐABD = 3a.
Построим луч BE так, чтобы ÐEBD = a. ТогдаÐABE = 2a = ÐAEB; BE = AE =ED = x.
Значит, ÐABD = 90º, ÐA = 60º, ÐABC = 120º.
Читайте также:
Рекомендуемые страницы:
©2015-2020 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-06-03
Нарушение авторских прав и Нарушение персональных данных
Источник
