Что такое внешний угол треугольника какими свойствами он обладает

Цели.

Знакомство учащихся с понятием внешнего угла
треугольника, с формулировкой определения;
рассмотреть свойство внешнего угла
треугольника; закрепить знания учащихся о сумме
углов треугольника и о внешнем угле треугольника
при решении задач.

Задачи.

1. Обучающая: обеспечить усвоение
материала всеми учащимися; учить и научить
каждого ученика самостоятельно добывать знания;
формировать навыки, умения, которые обеспечивают
успешное выполнение деятельности.

2. Развивающая: способствовать
развитию математического кругозора, мышления:
умения анализировать, выделять главное,
сравнивать, обобщать и систематизировать,
развивать устную и письменную речи, внимание и
память; продолжить работу по развитию умения
самостоятельно приобретать новые знания;
использование для достижения поставленной
задачи уже полученных знаний.

3. Воспитывающая: содействовать
воспитанию интереса к математике, активности,
дисциплинированности, честности,
ответственности за свой труд и труд
одноклассника, воспитание навыков самоконтроля
и взаимоконтроля.

Оборудование:

линейка, карандаш, треугольник;
компьютер, мультимедийный проектор,
интерактивная доска;
презентация.

Литература

Учебник Геометрия 7-9 классы: учеб. для
общеобразоват. учреждений Л.С. Атанасян, В.Ф.
Бутузов.
Уроки геометрии с применением информационных
технологий. 7-9 классы. Методическое пособие с
электронным приложением, / Е.М.Савченко. – 2-е
издание, стереотипное. Москва “Планета”, 2012.

Ход урока

I. Организационный момент

ІI. Активизация познавательной деятельности

Один из учащихся доказывает теорему о сумме
углов треугольника.
Второй учащийся решает на доске задачу № 230.
Устно со всем классом решаем задачи по готовым
чертежам.

Вычислить все неизвестные углы треугольника

Найдите неизвестный угол треугольника, если у
него два угла равны 50° и 60°. (Слайд 2, рисунок 1). Презентация
Найдите неизвестный угол треугольника, если у
него один угол прямой, а другой равен 20°. (Слайд 2,
рисунок 2)
Найдите угол при основании равнобедренного
треугольника, если угол между боковыми сторонами
40°. (Слайд 2, рисунок 3)
Найдите угол между боковыми сторонами
равнобедренного треугольника, если угол при
основании у него равен 30°. (Слайд 2, рисунок 4)
Вычислить все неизвестные углы прямоугольного
равнобедренного треугольника. (Слайд 3, рисунок 1)
Вычислить все неизвестные углы равностороннего
треугольника. (Слайд 3, рисунок 2)
Вычислите все неизвестные углы треугольников
(Слайд 4)
Определите вид треугольника (Слайды 5, 6, 7)

III. Изучение нового материала.

Вступительное слово учителя (постановка
проблемы урока).

Ребята, сегодня перед нами стоит такая
проблема: нам нужно познакомиться ещё с одним
углом, с которым мы раньше не встречались, у
которого так же есть своё свойство. Мы сегодня
повторили многие углы, которые мы знаем, и
некоторые из них помогут нам в решении нашей
поставленной задачи.

1. Ввести понятие внешнего угла треугольника:

Ребята, давайте выполним следующую
практическую работу, а именно:

Постройте произвольный треугольник АВС
Проведите луч ВД так, чтобы полученный угол
был смежным с углом В треугольника АВС.

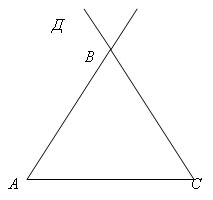
Что такое внешний угол треугольника какими свойствами он обладает

Назовите получившийся угол (может быть два
варианта АВД
или СВД)

Где они лежат по отношению к треугольнику,
внутри или вне его?

Эти углы имеют специальное название – они
называются внешними углами треугольника.

А теперь запишем тему урока “Внешний угол
треугольника и его свойство”

А как вы думаете, можно ли при других вершинах
этого треугольника построить внешние углы?

Итак, попробуем сформулировать определение
внешнего угла треугольника.

Вывод: Внешним углом треугольника называется
угол, смежный с каким-нибудь углом этого
треугольника.

IV. Физкультминутка.

а) Дыхательное упражнение.
б) Упражнение для позвоночника.
в) Упражнение для глаз.

Вывод: Внешний угол треугольника равен сумме
двух других углов треугольника, не смежных с ним.

Это и есть свойство внешнего угла треугольника,
и мы его вместе доказали.

V. Решение задач

1. Устно решить задачу: в треугольнике АВС =110°.

Чему равны:

а) сумма остальных внутренних углов
треугольника?

б) внешний угол при вершине С?

2. По готовому чертежу на доске устно решить
задачу:

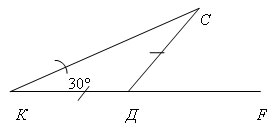
Что такое внешний угол треугольника какими свойствами он обладает

Найдите внутренние и внешний угол СДF
треугольника КСД.

3. Решить задачу № 232 под руководством учителя
на доске и в тетрадях.

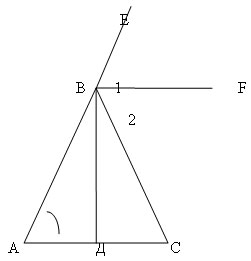
Что такое внешний угол треугольника какими свойствами он обладает

Дано: внешний угол треугольника АВС; .

Доказать: равнобедренный.

Решение

Проведем биссектрисы ВF и ВД смежных
углов СВЕ и АВС, тогда ВF || АС, так как , а углы 1 и А
соответственные при пересечении прямых ВF и АС секущей
АВ, ВД , так
как ВД , а
BF || AC.

В треугольнике АВС биссектриса ВД
является высотой, следовательно, треугольник АВС
– равнобедренный (см. задачу № 133)

2. Обратное утверждение также верно, а именно:
если треугольник равнобедренный, то внешний угол
при вершине, противолежащей основанию
треугольника, в два раза больше угла при
основанию Действительно, этот внешний угол равен
сумме двух углов при основании равнобедренного
треугольника, с так как углы при основании равны,
то данный внешний угол в два раза больше угла при
основании треугольника.

VI. Самостоятельная работа обучающего характера
(на четыре варианта)

Вариант 1

1. Один из углов равнобедренного треугольника
равен 96°. Найдите два других угла.

2. В треугольнике СДЕ с углом проведена биссектриса СF, . Найдите

Вариант 2

1. Один из углов равнобедренного треугольника
равен 108°. Найдите два других угла.

2. В треугольнике СДЕ проведена биссектриса СF,
,.

Найдите

Вариант 3

1. В равнобедренном треугольнике МNP c
основанием MP и углом проведена высота MH. Найдите .

2. В треугольнике СДЕ проведены биссектрисы СК
и ДР, пересекающиеся в точке F, причем Найдите

Вариант 4

1. В равнобедренном треугольнике СДЕ c
основанием СЕ и углом проведена высота СH. Найдите .

2. В треугольнике АВС проведены биссектрисы АМ
и BN, пересекающиеся в точке K, причем Найдите

VII. Домашнее задание: изучить пункты 30-31;
ответить на вопросы 1-5 на стр. 84; решить задачи №
233, 235.

VIII. Итоги урока

С чем мы сегодня познакомились?

– Что такое внешний угол треугольника?

– Какое свойство внешнего угла мы сегодня
доказали?

– Чему вы сегодня научились?

– Какие теоремы сегодня на уроке мы
использовали при решении задач?

IX. Рефлексия

Что такое внешний угол треугольника какими свойствами он обладает

Источник

Тема: «Внешние углы треугольника»

Тип урока: Ознакомление с новым материалом

Цели:

Познакомить учащихся с понятием внешнего угла
Доказать теорему о внешнем угле треугольника
Развить способность применять доказанную теорему в решении задач.

Ход урока

І . Устный опрос

Сформулировать теорему о сумме углов треугольника.
Найдите неизвестный угол треугольника, если у него два угла равны 50 ° и 30°.

50 °

30°

Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен 35°.

35°

Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами 80°.

80°

К
B
акие углы изображены на рисунке?

Какие углы называются смежными?
Каким свойством обладают смежные углы?
Найдите углы смежные с углами в 30°, 45°, 60°, 90°
Назовите смежные углы

Являются ли смежными AOB и DOC?

Найдите пары смежных углов на рисунке.

C какими углами не смежные DAB, EAC?

І. Изучение нового материала

– Постройте угол смежный с углом С.

– Угол, который вы построили, называется внешним углом ΔABC при вершине С.

Определение:

Внешним углом треугольника при данной вершине называется угол смежный с углом треугольника при этой вершине.

– Как вы думаете, можно ли еще построить внешний угол при вершине C?

– Что вы можете сказать о величине данных углов?

– Сколько всего внешних углов имеет треугольник?

Внешние углы треугольника обладают свойством, которые мы сегодня докажем.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

– Откройте учебник на стр. 66 и прочитайте внимательно.

– Где условие, где заключение?

– Что дано, что требовалось доказать?

Дано:

4 – внешний угол треугольника смежный с 3.

Доказать: 4 = 1+2

Доказательство:

– Чему равна сумма углов треугольника?

1. 1 + 2+3 = 180°

– Как найти сумму углов 1 и 2?

2. 1+ 2 = 180° – 3

– Как можно найти угол 4?

3. 4 = 180° – 3

– Что мы получим?

4. 4 = 1 + 2

ч.т.д.

– Какую теорему мы доказали?

ІІІ. Закрепление нового материала.

Пусть 4 = 70°. Чему равна сумма углов 1 и 2?
Сумма углов 1 и 2 равна 140°. Чему равен внешний угол не смежный с данными углами?

Задача 1. Внешний угол ABC при вершине C равен 120°. Найдите градусные меры углов треугольника, не смежные с ним, если известно, что один из них в 2 раза больше другого.

(с ребятами читаем еще раз условие задачи).

ано:

BCD = 120°

B > A в 2 раза

айдите: A и B

Решение:

Пусть A – х ° , тогда B = 2х° .

х +2х = 120

3х = 120

х =40 A = 40 °

B= 2 ·40° = 80°

Ответ: A = 40 °, B = 80°.

Задача 2. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине B равен 108°. Найдите углы треугольника.

Дано:

108°

Δ ABC- равнобедренный

AC – основание, DBC = 108°

Найдите: A, B, C

Решение:

DBC = A + C = 108° – по свойству внешних углов
A = C = 108° : 2 = 54° – по свойству равнобедренного треугольника
B = 180° – 108° = 72° – по свойству смежных углов

Ответ: A = 54°, С = 54°, B = 72°.

Итог:

– Какой угол называется внешним?

– Каким свойством обладает внешний угол треугольника?

Дополнительные задания:

Найдите углы равнобедренного треугольника, если внешний угол при основании равен 112°.

Ответ: 68°, 68°, 44°.

Найдите градусные меры внешних углов равностороннего треугольника.

Ответ: 120°, 120°, 120°.

Найдите внешний угол при основании равнобедренного треугольника с углом в 45°.

Ответ: 135°.

№

227 б)

Дано:

Δ ABC- равнобедренный

С < BCD

Найти углы Δ ABC

Решение:

Пусть С = х °, BCD = 3х°

Т.к. углы смежные и в сумме составляют 180°, то составим уравнение:

х + 3х = 180

4х = 180

х = 45

A = C = 45°

B = 90°.

Ответ: B = 90°.

ІV. Домашнее задание

п. 30, стр.66

B 1-2 стр.84

№233, №234, №235.

Источник

Основные определения

Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:

угла и треугольника;
смежных углов;
параллельных прямых.

Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.

Определение 1

Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.

На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.

Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ

Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.

Теорема о сумме углов треугольника

Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:

Теорема 1

Сумма углов треугольника равна $180^{circ}$.

Приведём её доказательство.

Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.

Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ

Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.

Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ

Видим, что углы 1 и 5 – накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.

Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.

Внешний угол треугольника

В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:

Определение 2

Внешний угол треугольника – это угол, являющийся смежным с каким-нибудь углом данного треугольника.

Имеем теорему:

Теорема 2

Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.

Докажем эту теорему.

Рассмотрим следующий рисунок:

Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ

Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:

$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.

Рассмотрим пример задачи на данную тему.

Пример 1

Задача. $triangle ABC$ – равнобедренный. $AC$ – основание этого треугольника. $AC$=37 см, внешний угол при $B$ равняется $60^{circ}$. Нужно найти расстояние от точки $C$ до прямой $AB$.

Решение. Сделаем рисунок:

Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ

На рисунке прямая, обозначающая расстояние от точки $C$ до прямой $AB$ обозначена как $CD$. В математике такое расстояние называют высотой. По определению высоты треугольника, прямая высоты перпендикулярна той стороне, на которую опущена. То есть $angle ADC = 90^{circ}$.

По теореме о внешнем угле треугольника находим $angle B$: $angle B=180-60=120^{circ}$. По теореме о сумме углов треугольника получается, что $angle A + angle C = 180-120=60$. Так как треугольник равнобедренный, углы у основания равны по $30^{circ}$.

Рассмотрим $triangle ADC$. Из вышеуказанного следует, что он прямоугольный. Из свойства прямоугольных треугольников известно, что катет такого треугольника, который лежит против угла $30^{circ}$, равен половине гипотенузы. В нашем случае, $СD$ является катетом против угла $30^{circ}$, а $AC$ – гипотенуза. Поэтому справедливо утверждать, что $CD=37/2=18,5$ см.

Ответ: 18,5 см.

Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.

Источник

Конспект урока математики

Основные дидактические цели урока:

сформировать потребность у учащихся в осуществлении творческого преобразования учебного материала с целью овладения новыми знаниями;
создать условия для закрепления знаний учащихся о сумме углов треугольника при решении задач, введения понятия внешнего угла треугольника, доказательства теоремы о внешнем угле треугольника;
сформировать у учащихся навык решения задач.

Структура урока:

актуализация знаний учащихся
введение понятия внешнего угла
доказательство теоремы о внешнем угле
отработка навыка решения задач
самостоятельная работа
итог урока

домашнее задание

В качестве эпиграфа к нашему уроку хочу привести слова великого русского поэта А.С. Пушкина «Вдохновение нужно в геометрии не меньше, чем в поэзии». Поэтому желаю вам вдохновения и хорошего настроения в работе.

Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырехтысячелетней давности. Китайцы гордятся китайским треугольником и считают, что он есть первоначалом всех фигур, и все остальные фигуры — лишь его частные случаи. Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов, а в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей.

Знает в мире каждый школьник,

Очень важен треугольник.

Ты на доску посмотри

И углы его найди.

Я предлагаю порешать задачи по готовым чертежам. Вычислите все известные углы треугольника

Какие из предложенных задач отличаются от других?
В чем это отличие ?

-Какая же тема сегодняшнего урока?

Вычислите все известные углы треугольника

– Даны углы вне треугольника.

Формирование понятия «внешний угол треугольника»

Фронтальная практическая работа.

Начертите в тетради треугольник АВС с углом В равным 110º и продолжите сторону АВ.

– Какой угол получили?

– Чему равны:

а) сумма остальных внутренних углов треугольника;

б) внешний угол при вершине В?

Попробуйте сформулировать определение внешнего угла треугольника.

Постройте внешние углы при вершинах А и С.

По готовому чертежу решаем задачу: в

равнобедренном треугольнике KDC с основанием СК, угол К равен 30º. Найти внутренние углы и внешний угол CDF треугольника КDC.

Что заметили? Сравните величину внешнего угла и сумму внутренних углов, не смежных с ним.
Сформулируйте теорему о внешнем угле треугольника.

внешний

70 º

70º

Формулируют определение.

Внешний угол равен сумме двух

углов треугольника, не смежных с ним.

Доказывают теорему.

Отработка навыка решения задач.

1.Решить задачу № 232 (на доске и в тетрадях).

Верно ли утверждение: если треугольник равнобедренный, то один из внешних углов в два раза больше угла треугольника, не смежного с этим внешним углом?

– Как будет формулироваться обратное утверждение?

– Верно ли обратное утверждение?

2.Решить задачу № 234 на доске и в тетрадях.

Один из внешних углов равнобедренного треугольника равен 115º. Найдите углы треугольника.

(рассмотреть два случая)

Дано: ∆АВС, <BCD больше < А в 2 раза.

Доказать: ∆АВС — равнобедренный.

Доказательство.

Примем <А = х, тогда <BCD = 2х.

По свойству внешнего угла:

< BCD = < A + < B, тогда

2х = х+ < B, тогда < В = х, значит,

< A = <B, т. е. ∆АВС — равнобедренный.

– Если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании.

Обратное утверждение верно.

Дано: ∆АВС, АВ=ВС, <BCD = 115º

Найти: < A, < B, <C.

Решение:

1.< C, <BCD – смежные. Значит,

<C = 180° – 115° = 65°.

<A = <C = 65°( по свойству равнобедренного треугольника)

3. < B = 180° – ( <A+ < C)

< B = 180° – 130° = 50°

Ответ : 65°, 65°, 50°.

Дано: ∆АВС, АВ=ВС,

Найти: < A, < B, <C.

Решение:

1.< B, <CBD — смежные, значит,

< В = 180° – 115°= 65°

2.Т. к. <A = <C ( по свойству равнобедренного треугольника), то

= (180° – 115°) :2 = 57,5 °= 57° 30´

Ответ: 65º, 57 º 30´, 57º 30´

– Итак, что мы узнали?

Научились ли мы применять свойство внешнего угла треугольника для решения задач?

Предлагаю самостоятельно решить задачи.

Поменяйтесь тетрадями, оцените работу соседа по парте.
У кого эти задачи вызвали затруднения?
Что именно вызвало затруднения?

Вариант 1.

1.Один из углов равнобедренного треугольника 96º. Найдите два других угла.

2.В ∆СDE c углом <Е = 32º проведена биссектриса CF, < CFD = 72 º . Найдите <D.

Вариант 2.

1.Один из углов равнобедренного треугольника 108º. Найдите два других угла.

2.В ∆СDE проведена биссектриса CF,

< D = 68 º , <E = 32º. Найдите <CFD.

Давайте вернемся к нашему плану.
Назовите все внешние углы треугольников, какие вы видите на слайде.
Каким свойством обладает внешний угол равнобедренного треугольника.
Оцените свою работу на уроке.

– дети называют внешние углы.

Запишите домашнее задание: п 30-31, № 235.

Источник