Граф с каким свойствами называют деревом что такое корень дерева
Корневые деревья
Произвольно зафиксируем
некоторую вершину дерева
и назовем
ее корнем дерева. Само дерево в этом случае будем называть деревом
с корнем или корневым деревом.
Иногда полезно, руководствуясь
какими–либо соображениями, выделять в дереве некоторую определенную цепь , которую обычно называют
стволом дерева. Корень дерева обычно является одной из концевых
вершин ствола. Каждая концевая вершина дерева связана с ближайшей вершиной ствола единственной цепью.
Эту цепь называют ветвью дерева, выходящей из вершины в вершину . При отсутствии у дерева
ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева
с его корнем.
Корневые деревья естественно
ориентировать, если в этом есть необходимость, от корня. Все
ребра, инцидентные корню дерева, считаются исходящими из корня и заходящими
в вершины, смежные корню. Все ребра дерева, инцидентные вершинам, удаленным
на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими
в вершины, им смежные. Процесс ориентации ребер продолжается подобным
образом до тех пор, пока не будут ориентированы все ребра дерева. Поученное
в результате такой ориентации дерево с корнем называется ориентированным
деревом. В нем все ребра имеют направление от корня. Если поменять
направления всех дуг ориентированного дерева на противоположные (к
корню), то получившийся в итоге ориентированный граф называют
сетью сборки.
На рис. 4. 38 приведены примеры дерева
с корнем ,
его ориентированного дерева и сети сборки .
Деревья графов
Пусть дерево является подграфом графа
.
Ребра графа , которые принадлежат дереву
,
называются ветвями дерева ,
а ребра, не принадлежащие дереву , –
хордами относительно дерева . Если есть суграф , то есть вершины дерева совпадают с вершинами графа , то говорят, что дерево
покрывает граф . В этом случае дерево называют остовом
или каркасом графа .
Существует простой способ определить количество
различных остовов мультиграфа с вершинами. Для этого нужно записать матрицу
размера
, по главной диагонали которой
выписаны степени вершин, а элементы равны взятому со знаком минус числу ребер,
связывающих вершины и
,
.
Вычислив минор любого элемента главной диагонали матрицы , получим искомое число возможных
остовов графа.
Например, для графа на рис. 4.39 имеем:
; .
Следовательно, существует
50 различных деревьев, покрывающих этот граф. Один из 50 остовов мультиграфа
изображен на рис. 4.39 жирными линиями.
Экстремальные графы
Класс практических задач, достаточно успешно решаемых
методами теории графов, требует связать пунктов наиболее экономичным образом. Например,
необходимо построить автомобильные дороги, связывающие дачных поселков, так, чтобы
их суммарная длина была наименьшей. Любые два поселка должны быть
связаны дорогой либо непосредственно, либо дорогами, проходящими через
другие поселки. Похожие задачи возникают при прокладке водопроводов,
газопроводов, линий связи и т. п.
На языке теории графов задачи такого рода формулируются
следующим образом. Каждому ребру полного графа с вершинами приписывается вес , выражающий численно расстояние,
стоимость или иную величину, характеризующую взаимосвязь между каждой
парой вершин графа. Требуется выявить такой остов этого графа, чтобы
суммарный вес ветвей остова был минимальным (или
максимальным). Такой остов графа называют его экстремальным
деревом.
Поскольку полный граф покрывает различных основных деревьев, то
решение этой задачи полным перебором вариантов потребовало бы чрезвычайно
больших вычислений даже при относительно малых . Уже при таких вариантов больше миллиона.
Для решения задач такого рода разработаны достаточно
эффективные алгоритмы. Далее мы воспользуемся одним из них – алгоритмом Дж. Краскала. Его суть состоит в следующем. На первом шаге выбирается
первая ветвь искомого остова – это ребро графа с
наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается
минимальное (максимальное) по весу ребро и, если оно не образует цикла
с ранее выбранными ветвями, вводится в остов. Построение заканчивается
после отбора для остова ребер.
Теорема 4.13. Алгоритм Краскала позволяет построить экстремальный
граф любого связного графа.
Пример 4.3. Необходимо построить автомобильные дороги, связывающие
девять поселков так, чтобы их суммарная длина была наименьшей. Любые
два поселка должны быть связаны дорогой либо непосредственно, либо
дорогами, проходящими через другие поселки. Известно расстояние между
поселками (в км):
На первом шаге выбираем самый короткий участок искомой сети дорог, связывающей
поселки. Это дорога длиною 12 км между поселками П1 и П2. Затем добавляем
к ней дороги между П1 и П3 (13 км), П1 и П9 (14 км), П5 и П7 (15 км),
П3 и П4 (18 км). Следующее минимальное расстояние между поселками
равно 19 км. Таково расстояние между П1 и П8 и между П6 и П7. Так
как обе эти дороги не образуют цикла с уже отобранными дорогами, то
обе они добавляются в список. Следующие по длине (25 км и 26 км) дороги
между П1, П2 и П5, П6 нельзя добавлять в наш список – иначе появятся циклы: П1, П2, П3, П2 или П5, П6, П7,
П5. Восьмая и последняя дорога искомого минимального остова имеет
длину 28 км, она проходит между П5 и П8. Минимальный остов, связывающий
девять поселков, изображен на рис. 4.40. Минимальная длина дорог, связывающих поселки, равна
138 км.
Рис.4.40
Экстремальное дерево может быть построено для произвольного графа, а не
только для полного графа. Например, связи между некоторыми вершинами
могут быть нежелательными или недопустимыми.
Источник
Дерево – это частный случай графа, наиболее широко применяемый в программировании.
Основные определения
Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.
Дерево – это связный граф без циклов.
Дерево – это связный граф, в котором при N вершинах всегда ровно N-1 ребро.
Дерево – это граф, между любыми двумя вершинами которого существует ровно один путь.
Аналогичным образом определяется и ориентированное дерево – как орграф, в котором между любыми двумя вершинами существует не более одного пути.
Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющей циклов.
Для каждой пары вершин дерева – узлов – существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины.
Расстояние до корневой вершины V0 называется ярусом s вершины.
Поскольку маршрут между двумя вершинами единственный, то , применяя это свойство к смежным вершинам, можно заключить, что любая ветвь является мостом.
При удалении ребра единственный маршрут прерывается и граф распадается на два подграфа.
Корневое дерево – это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;
в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья “растут” вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья – самыми нижними.
Предок вершины v – это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v – это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево – это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева – это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота – это просто расстояние от корня до самого удаленного листа.
Свойства деревьев.
Граф G(V,X) является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:
1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.
2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.
3. Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.
4. Граф G(V,X) связен и не содержит циклов.
5. Граф G(V,X) связный , но утрачивает это свойство после удаления любого ребра.
Итак, дерево с n вершинами имеет n-1 ребро, поэтому оно будет минимальным связным графом.
Висячие вершины, за исключением корневой, называют листьями.
Остовом связного графа называется любой его подграф , содержащий все вершины графа и являющийся деревом.
Подграф G1 = (V1, E1) графа G = (V, E), называется остовным деревом в
графе G = (V, E), если G1 = (V1, E1) — дерево и V1 = V.
Источник
Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
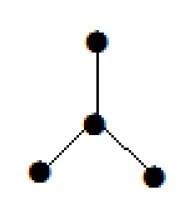
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
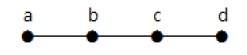
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
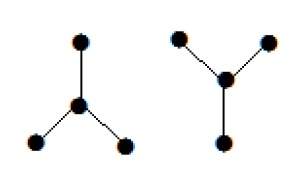
Охватывающие деревья
Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —
- H это дерево
- H содержит все вершины G.
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
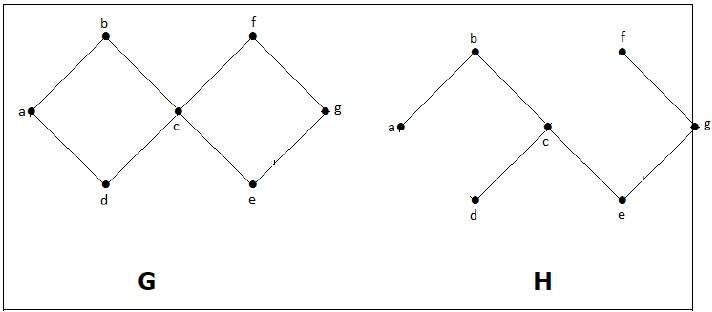
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график —
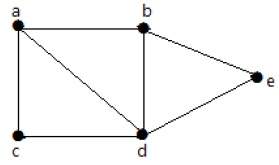
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
Тогда ранг цепи
G = m – (n – 1)
= 7 – (5 – 1)
= 3
пример
Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
n ∑ i = 1 градус (V i ) = 2 | E |
6 × 3 = 2 | E |
| E | = 9
Схема ранг = | E | — (| V | — 1)
= 9 — (6 — 1) = 4
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
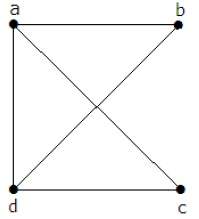
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
Задача коммивояжера, задача о минимальной раскраске графа.
Деревья. Свободные деревья. Основные свойства деревьев.
Граф без циклов называют ациклическим или лесом. Связный ациклический граф называют деревомили свободным деревом. Компонентами связности леса являются деревья.
В связном графе выполняется неравенство , где – количество ребер, – количество вершин. Граф , в котором выполняется равенство называют древовидным.
В ациклическом графе число циклов . Пусть – несмежные вершины графа и пусть – ребро, которое может быть образовано между вершинами и , не принадлежит множеству ребер графа , . Если граф имеет только один простой цикл, , то граф называется субциклическим.
Пример: свободные деревья с пятью вершинами.
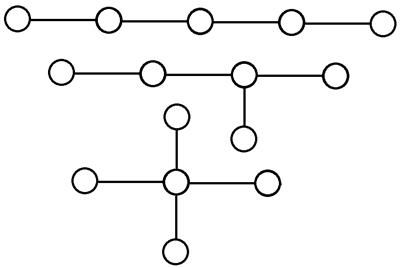
Свойства деревьев.
Теорема о свойствах деревьев устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.
Теорема.Пусть – граф с вершинами, ребрами, компонентами связности и простыми циклами. Пусть – ребро, соединяющее любую пару несмежных вершин в графе . Тогда следующие утверждения эквивалентны:
1. – дерево, т.е. связный граф без циклов,
;
2. Любые две вершины соединены в графе единственной простой цепью,
;
3. – связный граф, и любое ребро есть мост,
;
4. Граф – связный и древовидный,
;
5. Граф – ациклический и древовидный,
;
6. Граф – ациклический и субциклический,
;
7. Граф – связный, субциклический и неполный,
;
8. Граф – древовидный и субциклический (за двумя исключениями),
.
Ориентированные деревья.
Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:
1. Существует единственный узел , полустепень захода которого равна 0, . Он называется корнемордерева.
2. Полустепень захода всех остальных узлов равна единице, .
3. Каждый узел достижим из корня, .
Пример: диаграммы ордеревьев с 3 узлами:
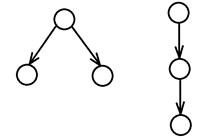
диаграммы ордеревьев с 4 узлами:
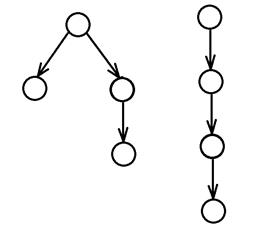
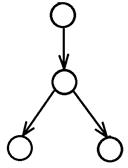
Свойства ордерева:
1. Число ребер на единицу меньше числа узлов, .
2. Если в ордереве забыть ориентацию ребер то получится свободное дерево.
3. В ордереве нет контуров.
4. Для каждого узла существует единственный путь, ведущий в этот узел из корня.
5. Подграф, определяемый множеством узлов, достижимых из узла , является ордеревом с корнем (это ордерево называется поддеревом узла ).
6. Если в свободном дереве любую вершину назначить корнем, то получится ордерево.
Эквивалентное определение ордерева.
Ордерево – это конечное множество узлов, таких что:
1. Имеется один узел , называемый корнем данного дерева.
2. Остальные узлы (исключая корень) содержатся в попарно непересекающихся множествах , каждое из которых является ордеревом.
.
Если относительный порядок поддеревьев фиксирован, то ордерево называется упорядоченным.
Пример: для представления выражений языков программирования, как правило, используются ориентированные упорядоченный деревья. Выражение :
Бинарные деревья.
Бинарное (двоичное) дерево– это конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев – левого и правого. Бинарное дерево не является упорядоченным ордеревом.
Пример: два различных бинарных дерева.
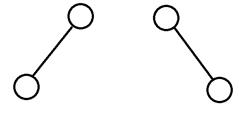
Всякое свободное дерево можно ориентировать, назначив один из узлов корнем. Всякое ордерево можно произвольно упорядочить. Для потомков одного узла (братьев) упорядоченного ордерева определено отношение старше-младше (левее-правее). Всякое упорядоченное дерево можно представить бинарным деревом, проведя правую связь к старшему брату, а левую – к младшему сыну.
Пример: диаграммы упорядоченного и соответствующего ему бинарного дерева.
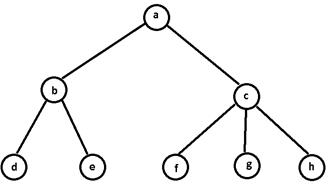

упорядоченное дерево бинарное дерево
Эйлеровы графы.
Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называют эйлеровым циклом, а граф называют эйлеровым графом.
Если граф имеет цепь (не обязательно простую), содержащую все ребра по одному разу, то такая цепь называется эйлеровой цепью, а граф называют полуэйлеровым графом.
Теорема.Если граф связен и нетривиален, то следующие утверждения эквивалентны:
1. – эйлеров граф.
2. Каждая вершина графа имеет четную степень.
3. Множество ребер графа можно разбить на простые циклы.
Теорема дает решение задачи о кенигсбергских мостах. Т.е. для того чтобы обойти все ребра по одному разу – степени все вершин должны быть четны.
Источник
Дерево – связный граф с n-1 ребром.
bool dfs(int i, int arr[SIZE][SIZE], bool col[SIZE]) {
if (col[i]) {
return 0;
}
col[i] = true;
for (int j = 0; j < SIZE; ++j) {
if (ar[i][j]) {
dfs(j, arr, col);
}
}
}
bool IsTree(int arr[SIZE][SIZE]) {
int edges = 0;
for (int i = 0; i < SIZE; ++i) {
for (int j = i + 1; j < SIZE; ++j) {
if (arr[i][j]) {
edges++;
}
}
}
if (edges != SIZE – 1) {
return false;
}
bool col[SIZE];
memset(col, 0, sizeof(col));
dfs(0, arr, col);
for (int i = 0; i < SIZE; ++i) {
if (!col[i]) {
return false;
}
}
return true;
}
ответ дан 18 янв ’11 в 11:07
wingerwinger
52222 серебряных знака88 бронзовых знаков
Моё решение на Pascal. Граф задаётся матрицей смежности (1 – есть ребро, 0 – иначе).
maxV – максимальное число вершин
maxE – максимальное число рёбер
Храню граф списком рёбер.
const
maxV = 111;
maxE = 111111*2;
var
n,m,i,j,x : longint;
ef,es,next : array [1..maxE] of longint;
first,last : array [1..maxV] of longint;
c : longint;
used : array [1..maxV] of boolean;
flag : boolean;
procedure add(v1,v2 : longint);
begin
inc(c);
ef[c] := v1; es[c] := v2;
if last[v1] <> 0 then next[last[v1]] := c;
if first[v1] = 0 then first[v1] := c;
last[v1] := c;
end;
procedure dfs(v,dad : longint);
var
h,e : longint;
begin
used[v] := true;
h := first[v];
while h > 0 do begin
e := es[h];
if used[e] and (e <> dad) then begin
flag := false;
exit;
end;
if e <> dad then
dfs(e,v);
if not flag then
exit;
h := next[h];
end;
end;
begin
assign(input,’input.txt’); reset(input);
assign(output,’output.txt’); rewrite(output);
readln(n);
for i := 1 to n do
for j := 1 to n do begin
read(x);
if x = 1 then
add(i,j);
end;
flag := true;
dfs(1,1);
for i := 1 to n do
if not used[i] then
flag := false;
if not flag then
writeln(‘NO’)
else
writeln(‘YES’);
end.
ответ дан 7 мая ’11 в 13:33
megacodermegacoder
3,0292323 серебряных знака4747 бронзовых знаков
Есть несколько способов решения. Можно использовать свойство ацикличности с подсчетом количества вершин, те обходим граф в ширину/глубину, подсчитывая число обойденных вершин, если мы обошли граф и не встретили ни одну вершину два раза, а также общее количество вершин и число обойденных вершин равны, то это дерево .
ответ дан 18 янв ’11 в 15:00
Nicolas Chabanovsky♦Nicolas Chabanovsky
47.4k6565 золотых знаков237237 серебряных знаков461461 бронзовый знак
Выполняем обычный проход по графу и каждую пройденный узел заносим в список, при этом проверяем не содержится ли он в нем уже. Если содержится то всё не дерево 🙂
ответ дан 18 янв ’11 в 14:15
psyhituspsyhitus
3,46122 золотых знака1616 серебряных знаков2929 бронзовых знаков
Всё ещё ищете ответ? Посмотрите другие вопросы с метками алгоритм графы дерево или задайте свой вопрос.
Источник
