Граф с какими свойствами называется деревом
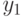
Дерево – это частный случай графа, наиболее широко применяемый в программировании.
Основные определения
Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.
Дерево – это связный граф без циклов.
Дерево – это связный граф, в котором при N вершинах всегда ровно N-1 ребро.
Дерево – это граф, между любыми двумя вершинами которого существует ровно один путь.
Аналогичным образом определяется и ориентированное дерево – как орграф, в котором между любыми двумя вершинами существует не более одного пути.
Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющей циклов.
Для каждой пары вершин дерева – узлов – существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины.
Расстояние до корневой вершины V0 называется ярусом s вершины.
Поскольку маршрут между двумя вершинами единственный, то , применяя это свойство к смежным вершинам, можно заключить, что любая ветвь является мостом.
При удалении ребра единственный маршрут прерывается и граф распадается на два подграфа.
Корневое дерево – это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;
в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья “растут” вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья – самыми нижними.
Предок вершины v – это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v – это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево – это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева – это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота – это просто расстояние от корня до самого удаленного листа.
Свойства деревьев.
Граф G(V,X) является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:
1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.
2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.
3. Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.
4. Граф G(V,X) связен и не содержит циклов.
5. Граф G(V,X) связный , но утрачивает это свойство после удаления любого ребра.
Итак, дерево с n вершинами имеет n-1 ребро, поэтому оно будет минимальным связным графом.
Висячие вершины, за исключением корневой, называют листьями.
Остовом связного графа называется любой его подграф , содержащий все вершины графа и являющийся деревом.
Подграф G1 = (V1, E1) графа G = (V, E), называется остовным деревом в
графе G = (V, E), если G1 = (V1, E1) — дерево и V1 = V.
Источник
4.3. Деревья и лес
Свойства деревьев
Определение 4.12. Граф
называется
деревом, если он связный и не имеет циклов.
Лесом называют граф, связные компоненты которого являются деревьями.
В частности, дерево не может иметь петель и кратных ребер.
Вершину графа, инцидентную только одному его ребру,
называют концевой (или висячей) вершиной,
а ребро, инцидентное концевой вершине, будем называть концевым ребром
графа.
Среди различных деревьев выделяют два важных частных
случая: последовательное дерево, представляющее собой простую
цепь, и звездное дерево (или куст), в котором одна из вершин
(центр) смежна со всеми остальными вершинами.
Пусть множество содержит вершин. Связав эти вершины
ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее
данное множество вершин. Для двух вершин существует одно покрывающее дерево
– сами вершины и ребро, их связывающее. С увеличением
число различных
деревьев быстро
увеличивается:
.
Деревья считаются существенно
различными, если они не изоморфны. Всего деревьев с четырьмя вершинами
16, из них существенно различных только 2; деревьев с шестью вершинами 1296,
а существенно различных всего 6, но уже при насчитывается около миллиона существенно различных
деревьев.. На рис. 4.34 приведены существенно различные деревья с четырьмя и
с шестью вершинами:
Среди графов n-го порядка (с n вершинами) без кратных
ребер полный граф имеет наибольшее количество ребер, а дерево
(n-го порядка) – наименьшее. Дерево содержит минимальное количество
ребер, необходимое для того, чтобы граф был связным.
Теорема 4.9. Каждое
дерево с вершинами
имеет в точности ребро.
► Действительно, две
вершины связываются одним ребром, и для связи каждой добавляемой вершины с
одной из уже имеющихся вершин необходимо еще одно ребро. Если же добавить
два ребра, то есть соединить новую вершину с двумя вершинами, из уже рассмотренных
вершин, то обязательно образуется цикл. Следовательно, для минимальной связи
вершин необходимо
и достаточно ребер. ◄
Нетрудно убедиться в справедливости
следующих теорем.
Теорема 4.10. Граф
является деревом тогда и только тогда, когда каждая пара различных вершин
графа соединяется одной и только одной простой цепью.
Теорема 4.11. У
каждого дерева найдется висячая вершина.
Теорема 4.12. При
удалении любого ребра дерева
оно распадается на связные компоненты, являющиеся либо изолированными вершинами,
либо деревьями. При добавлении в дерево любого нового ребра в нем образуется
простой цикл, и оно перестает быть деревом.
Дерево на рис. 4. 35 при
удалении ребра распадается
на лес из двух деревьев и , а после добавления ребра превращается в циклический
граф .
Рассматриваются также
деревья с ориентированными ребрами (дугами). Ориентированное дерево называется
прадеревом с корнем ,
если существует простой путь между вершиной и любой
другой его вершиной (рис. 4.36). Прадерево может иметь только один корень.
Типы вершин
дерева и его центры
Рассмотрим
дерево с
вершинами. Назовем его
концевые вершины вершинами типа 1. Теперь удалим все вершины типа
1 и концевые ребра. В результате получим связный граф без циклов , то есть опять дерево,
но с уже меньшим количеством вершин. Концевые вершины дерева назовем вершинами типа
2 в дереве .
Аналогично определяются вершины типов 3, 4 и т. д. Легко видеть, что дерево
может иметь либо одну вершину максимального типа, либо две таких вершины.
Типы вершин дерева ,
изображенного на рис. 4. 37, записаны рядом
с соответствующими вершинами. Здесь же показаны последовательные этапы процедуры,
позволяющей их определить. Это дерево имеет две вершины максимального типа.
Если у дерева удалить
одну из вершин типа 2 и ребра, ей инцидентные, то получившееся при этом
дерево будет иметь уже только одну вершину максимального типа.
Пусть вершина типа k
есть вершина максимального
типа. Из определения типа вершин дерева следует, что эксцентриситет
единственной вершины максимального типа равен ее типу, то есть равен
k, а
эксцентриситет каждой из двух вершин максимального типа равен k-1. При этом эксцентриситет
любой вершины не максимального типа будет обязательно больше. Поэтому
центрами любого дерева являются его вершины максимального типа, следовательно,
дерево имеет либо один, либо два центра. Нетрудно убедиться, что диаметральные
цепи в деревьях проходят через его центр или через оба центра, если
их два. В первом случае длина диаметральной цепи равна
2k-2, а во втором 2k-1.
Источник
Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
Охватывающие деревья
Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —
- H это дерево
- H содержит все вершины G.
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график —
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
Тогда ранг цепи
G = m – (n – 1)
= 7 – (5 – 1)
= 3
пример
Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
n ∑ i = 1 градус (V i ) = 2 | E |
6 × 3 = 2 | E |
| E | = 9
Схема ранг = | E | — (| V | — 1)
= 9 — (6 — 1) = 4
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
Аннотация: Деревья. Центр дерева. Корневые деревья. Каркасы. Двудольные графы.
Планарные графы.
Деревья
Деревом называется связный граф,
не имеющий циклов. В графе без
циклов, таким образом, каждая компонента связности является деревом.
Такой граф называют лесом.
Из теоремы 2
“Маршруты, связность, расстояния”
следует, что во всяком дереве, в котором не
меньше двух вершин, имеется вершина степени 1. Такие вершины называют висячими вершинами, или листьями. В действительности
легко
доказать, что в каждом дереве не меньше двух листьев, а цепь –
пример дерева, в котором точно два листа.
В следующих двух теоремах устанавливаются некоторые свойства деревьев.
Теорема 1. Граф с вершинами и ребрами является деревом
тогда
и только тогда, когда он
удовлетворяет любым двум из следующих трех условий:
- (1) связен;
- (2) не имеет циклов;
- (3) .
Доказательство.
Первые два условия вместе составляют определение
дерева. Покажем, что выполнение любых двух из условий (1)-(3) влечет
за собой выполнение третьего.
(1) и (2) (3). Индукция по числу вершин. При
утверждение очевидно. При в дереве имеется хотя бы один
лист.
Если из дерева удалить лист, то снова получится дерево, так как циклов не
появится, а связность, очевидно, сохранится. В этом новом дереве
вершин и, по предположению индукции, ребра. Следовательно,
в исходном дереве было ребро.
(2) и (3) (1). Пусть в графе, не имеющем циклов,
ребро, а его компонентами связности являются ,
причем состоит из вершин, .
Каждая компонента является деревом, поэтому, как доказано выше, число
ребер в равно , а всего ребер в
графе .
Значит, и граф связен.
(1) и (3) (2). Рассмотрим связный граф
с ребром.
Если бы в нем был цикл, то, удалив любое цикловое ребро, мы получили бы
связный граф с меньшим числом ребер. Можно продолжать такое удаление ребер
до тех пор, пока не останется связный граф без циклов, то есть дерево.
Но ребер в этом дереве было бы меньше, чем , а это противоречит
доказанному выше.
Теорема 2. Если – дерево, то
- в любая пара вершин соединена единственным
путем; - при добавлении к любого нового ребра образуется
цикл; - при удалении из любого ребра он превращается
в несвязный граф.
Доказательство.
Существование пути между любыми двумя вершинами
следует из связности дерева. Допустим, что в некотором дереве существуют
два различных пути, соединяющих вершины и .
Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той
же вершине ). Пусть – последняя вершина
этого совпадающего
начала, а после в одном пути следует
вершина ,
а в другом – вершина . Рассмотрим ребро .
Если его удалить из графа, то в оставшемся подграфе вершины
и будут соединимыми – соединяющий их маршрут можно
построить так:
взять отрезок первого пути от до и к нему
присоединить
отрезок второго от до , взятый в обратном
порядке. Но это
означает, что ребро не является перешейком.
Однако из теоремы 4
“Маршруты, связность, расстояния”
следует, что в дереве каждое ребро
является перешейком. Этим доказано утверждение 1). Утверждения 2) и 3)
следуют из 1).
Отметим, что единственный путь, соединяющий две вершины дерева, всегда
простой (если путь не является простым, в нем обязательно содержится
цикл).
Источник
Дерево — это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]
Формально дерево определяется как конечное множество одного или более узлов со следующими свойствами:
- существует один корень дерева
- остальные узлы (за исключением корня) распределены среди непересекающихся множеств , и каждое из множеств является деревом; деревья называются поддеревьями данного корня
Связанные определения
- Степень узла — количество исходящих дуг (или, иначе, количество поддеревьев узла).
- Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).
- Узел ветвления — неконцевой узел.
- Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
- уровень корня дерева равен 0;
- уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева , содержащего данный узел.
- Дерево с отмеченной вершиной называется корневым деревом.
- Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
- Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
Двоичное дерево

Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (оно же бинарное дерево) имеет несколько значений:
- Неориентированное дерево, в котором степени вершин не превосходят 3.
- Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
- Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.
N-арные деревья
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
- N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
- N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.
Свойства
Подсчёт деревьев
для числа неизоморфных корневых деревьев с вершинами удовлетворяет функциональному уравнению
.
- Производящая функция
для числа неизоморфных деревьев с вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
- При верна следующая асимптотика
где и определённые константы, , .
Кодирование деревьев
Дерево можно кодировать наборами из нулей и единиц. Рассмотрим, например, укладку дерева на плоскости. Начиная с какой либо вершины, будем двигаться по ребрам дерева, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах дерева. Проходя по некоторому ребру, записываем при движении по ребру в первый раз и при движении по ребру второй раз (в обратном направлении). Если — число рёбер дерева, то через шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из и (код дерева) длины позволяет однозначно восстанавливать не только само дерево , но и его укладку на плоскости. Произвольному дереву соответствуют несколько таких кодов. В частности, из этого способа кодирования вытекает следующая грубая оценка на число деревьев с вершинами:
См. также
- Словарь терминов теории графов
- Лес непересекающихся множеств
Примечания
- ↑ § 13. Определение дерева // Лекции по теории графов / Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И.. — М.: Наука, Физматлит, 1990. — С. 53. — 384 с. — 22 000 экз. — ISBN 5-02-013992-0
- ↑ Альфс Берзтисс. Глава 3. Теория графов. 3.6. Деревья // Структуры данных = A. T. Berztiss. Data structures. Theory and practice. — М.: Статистика, 1974. — С. 131. — 10 500 экз.
- ↑ Дискретная математика: алгоритмы. Формула Кэли
Литература
- Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4
- Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
Источник
