Граф с какими свойствами называют деревом что такое корень дерева ветви листья

Дерево — это связный ациклический граф.[1] Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.

Лес — множество деревьев.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]

Связанные определения[править | править код]

Степень вершины — количество инцидентных ей ребер.

Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).

Узел ветвления — неконцевой узел.

Дерево с отмеченной вершиной называется корневым деревом.

Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:

уровень корня дерева равен 0;
уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева , содержащего данный узел.

Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.

Несводимым называется дерево, в котором нет вершин степени 2.

Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.

Двоичное дерево[править | править код]

Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.

Термин двоичное дерево (применяется так же термин бинарное дерево) имеет несколько значений:

Неориентированное дерево, в котором степени вершин не превосходят 3.
Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.

N-арные деревья[править | править код]

N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.

N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.

Свойства[править | править код]

Подсчёт деревьев[править | править код]

для числа неизоморфных корневых деревьев с вершинами удовлетворяет функциональному уравнению
.

Производящая функция

для числа неизоморфных деревьев с вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:

При верна следующая асимптотика

где и определённые константы, , .

Кодирование деревьев[править | править код]

Дерево можно задать в виде стpоки, содержащей символы, помечающие вершины деpева, а также открывающие и закрывающие кpуглые скобки. Между деpевьями и их линейными скобочными записями существует взаимно однозначное соответствие.

См. также[править | править код]

Глоссарий теории графов
Лес непересекающихся множеств
Список структур данных (деревья)

Примечания[править | править код]

↑ § 13. Определение дерева // Лекции по теории графов / Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И.. — М.: Наука, Физматлит, 1990. — С. 53. — 384 с. — 22 000 экз. — ISBN 5-02-013992-0.
↑ Альфс Берзтисс. Глава 3. Теория графов. 3.6. Деревья // Структуры данных = A. T. Berztiss. Data structures. Theory and practice. — М.: Статистика, 1974. — С. 131. — 10 500 экз.
↑ Дискретная математика: алгоритмы. Формула Кэли (недоступная ссылка). Дата обращения 29 октября 2009. Архивировано 14 июня 2009 года.

Литература[править | править код]

Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4.
Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
Харари Ф. Теория графов. — М.: Мир, 1973. — 302 с.

Источник

Корневые деревья

Произвольно зафиксируем
некоторую вершину дерева
и назовем
ее корнем дерева. Само дерево в этом случае будем называть деревом
с корнем или корневым деревом.

Иногда полезно, руководствуясь
какими–либо соображениями, выделять в дереве некоторую определенную цепь , которую обычно называют
стволом дерева. Корень дерева обычно является одной из концевых
вершин ствола. Каждая концевая вершина дерева связана с ближайшей вершиной ствола единственной цепью.
Эту цепь называют ветвью дерева, выходящей из вершины в вершину . При отсутствии у дерева
ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева
с его корнем.

Корневые деревья естественно
ориентировать, если в этом есть необходимость, от корня. Все
ребра, инцидентные корню дерева, считаются исходящими из корня и заходящими
в вершины, смежные корню. Все ребра дерева, инцидентные вершинам, удаленным
на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими
в вершины, им смежные. Процесс ориентации ребер продолжается подобным
образом до тех пор, пока не будут ориентированы все ребра дерева. Поученное
в результате такой ориентации дерево с корнем называется ориентированным
деревом. В нем все ребра имеют направление от корня. Если поменять
направления всех дуг ориентированного дерева на противоположные (к
корню), то получившийся в итоге ориентированный граф называют
сетью сборки.

На рис. 4. 38 приведены примеры дерева
с корнем ,
его ориентированного дерева и сети сборки .

Деревья графов

Пусть дерево является подграфом графа
.
Ребра графа , которые принадлежат дереву
,
называются ветвями дерева ,
а ребра, не принадлежащие дереву , –
хордами относительно дерева . Если есть суграф , то есть вершины дерева совпадают с вершинами графа , то говорят, что дерево
покрывает граф . В этом случае дерево называют остовом
или каркасом графа .

Существует простой способ определить количество
различных остовов мультиграфа с вершинами. Для этого нужно записать матрицу
размера
, по главной диагонали которой
выписаны степени вершин, а элементы равны взятому со знаком минус числу ребер,
связывающих вершины и
,
.
Вычислив минор любого элемента главной диагонали матрицы , получим искомое число возможных
остовов графа.
Например, для графа на рис. 4.39 имеем:

; .

Следовательно, существует
50 различных деревьев, покрывающих этот граф. Один из 50 остовов мультиграфа
изображен на рис. 4.39 жирными линиями.

Экстремальные графы

Класс практических задач, достаточно успешно решаемых
методами теории графов, требует связать пунктов наиболее экономичным образом. Например,
необходимо построить автомобильные дороги, связывающие дачных поселков, так, чтобы
их суммарная длина была наименьшей. Любые два поселка должны быть
связаны дорогой либо непосредственно, либо дорогами, проходящими через
другие поселки. Похожие задачи возникают при прокладке водопроводов,
газопроводов, линий связи и т. п.

На языке теории графов задачи такого рода формулируются
следующим образом. Каждому ребру полного графа с вершинами приписывается вес , выражающий численно расстояние,
стоимость или иную величину, характеризующую взаимосвязь между каждой
парой вершин графа. Требуется выявить такой остов этого графа, чтобы
суммарный вес ветвей остова был минимальным (или
максимальным). Такой остов графа называют его экстремальным
деревом.

Поскольку полный граф покрывает различных основных деревьев, то
решение этой задачи полным перебором вариантов потребовало бы чрезвычайно
больших вычислений даже при относительно малых . Уже при таких вариантов больше миллиона.

Для решения задач такого рода разработаны достаточно
эффективные алгоритмы. Далее мы воспользуемся одним из них – алгоритмом Дж. Краскала. Его суть состоит в следующем. На первом шаге выбирается
первая ветвь искомого остова – это ребро графа с
наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается
минимальное (максимальное) по весу ребро и, если оно не образует цикла
с ранее выбранными ветвями, вводится в остов. Построение заканчивается
после отбора для остова ребер.

Теорема 4.13. Алгоритм Краскала позволяет построить экстремальный
граф любого связного графа.

Пример 4.3. Необходимо построить автомобильные дороги, связывающие
девять поселков так, чтобы их суммарная длина была наименьшей. Любые
два поселка должны быть связаны дорогой либо непосредственно, либо
дорогами, проходящими через другие поселки. Известно расстояние между
поселками (в км):

На первом шаге выбираем самый короткий участок искомой сети дорог, связывающей
поселки. Это дорога длиною 12 км между поселками П1 и П2. Затем добавляем
к ней дороги между П1 и П3 (13 км), П1 и П9 (14 км), П5 и П7 (15 км),
П3 и П4 (18 км). Следующее минимальное расстояние между поселками
равно 19 км. Таково расстояние между П1 и П8 и между П6 и П7. Так
как обе эти дороги не образуют цикла с уже отобранными дорогами, то
обе они добавляются в список. Следующие по длине (25 км и 26 км) дороги
между П1, П2 и П5, П6 нельзя добавлять в наш список – иначе появятся циклы: П1, П2, П3, П2 или П5, П6, П7,
П5. Восьмая и последняя дорога искомого минимального остова имеет
длину 28 км, она проходит между П5 и П8. Минимальный остов, связывающий
девять поселков, изображен на рис. 4.40. Минимальная длина дорог, связывающих поселки, равна
138 км.

Рис.4.40

Экстремальное дерево может быть построено для произвольного графа, а не
только для полного графа. Например, связи между некоторыми вершинами
могут быть нежелательными или недопустимыми.

Источник

Центр дерева

Центр графа может состоять из одной вершины (как, например, в графе 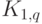$K_{1,q}$ ), а может включать все его вершины (полный граф). Для
дерева,
как мы увидим, имеется гораздо более узкий диапазон возможностей.

Теорема 3. Центр дерева состоит из одной вершины или из двух
смежных вершин.

Доказательство.

Допустим, что в некотором дереве имеются две
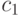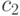несмежные центральные вершины $c_{1}$ и $c_{2}$ . На
пути,
соединяющем эти вершины, найдем промежуточную вершину с
максимальным
эксцентриситетом, и пусть $b_{1}$ и $b_{2}$ –
вершины, соседние
с на этом пути (см. рис. 3.1).
Пусть – вершина, наиболее удаленная
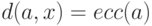от в дереве, т.е. d(a,x)=ecc(a) . Путь,
соединяющий с ,
не может проходить через обе вершины $b_{1}$
и $b_{2}$ . Допустим,
он не проходит через $b_{1}$ . Тогда единственный путь из $b_{1}$
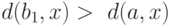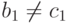в проходит через и $d(b_{1},x) gt d(a,x)$ . Отсюда следует, что $ecc(b_{1} ) gt ecc(a)$ , а это противоречит выбору вершины , если $b_{1} ne c_{1}$ , или тому, что $c_{1}$ –
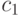центральная вершина, если $b_{1} =c_{1}$ .

Следовательно, любые две центральные вершины смежны, а так как в дереве
не может быть трех попарно смежных вершин, то в нем не больше двух
центральных вершин.

Рис.
3.1.

Корневые деревья

Часто в дереве особо выделяется одна вершина, играющая роль своего рода
“начала отсчета”. Дерево с выделенной вершиной называют корневым
деревом, а саму эту вершину – корнем. Из дерева с вершинами
можно, таким образом, образовать различных корневых
деревьев.

При графическом изображении корневого дерева обычно придерживаются
какого-нибудь стандарта. Один из наиболее распространенных состоит
в следующем. Возьмем на плоскости семейство параллельных прямых с равными
расстояниями между соседними прямыми. Изобразим корень точкой на одной из
этих прямых, смежные с корнем вершины – точками на соседней прямой,
вершины, находящиеся на расстоянии 2 от корня, – на следующей, и т.д.
Ребра изобразим отрезками прямых. Ясно, что вершины на каждой прямой можно
разместить так, чтобы ребра не пересекались. Пример нарисованного таким
образом корневого дерева показан на рис. 3.2 (корень обведен кружком). Чаще, впрочем, дерево рисуют корнем
вверх, а не вниз.

Рис.
3.2.

Иногда бывает полезно ребра корневого дерева ориентировать так, чтобы
в каждую вершину вел ориентированный путь из корня (для дерева
на рис. 3.2 это означает, что
каждое ребро
ориентируется снизу вверх). Такое
ориентированное корневое дерево будем называть исходящим деревом.
В исходящем дереве каждая вершина, кроме корня, является концом
единственного ребра. Если в исходящем дереве имеется ребро ,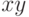
то вершину называют отцом вершины , а вершину – сыном
вершины . Естественный и для многих
целей удобный способ задания корневого дерева состоит в указании для
каждой вершины ее отца. При этом иногда считают, что корень приходится
отцом самому себе – это равносильно добавлению петли при корне.

Если в исходящем дереве имеется ориентированный путь из
вершины в вершину , то говорят, что – предок ,
а – потомок . В частности, каждая вершина
является предком и потомком самой себя. Множество всех предков
вершины порождает ориентированный путь из корня
в . Множество всех
потомков вершины порождает исходящее дерево с корнем
в ,
оно называется ветвью
дерева в вершине .

Высотой корневого дерева
называется эксцентриситет его корня. Если
мы хотим превратить некоторое дерево в корневое и притом минимальной
высоты, то в качестве корня следует взять центральную вершину.

Каркасы

Пусть – обыкновенный граф. Его каркасом называется
остовный подграф, в котором нет циклов, а области связности совпадают
с областями связности графа . Таким образом, каркас связного
графа –
дерево, а в общем случае – лес.

У любого графа есть хотя бы один каркас. Действительно, если
в
нет циклов, то он сам является собственным каркасом. Если же циклы есть,
то можно удалить из графа любое ребро, принадлежащее какому-нибудь циклу.
Такое ребро не является перешейком, поэтому при его удалении области
связности не изменятся. Продолжая действовать таким образом, после
удаления некоторого количества ребер получим остовный подграф, в котором
циклов уже нет, а области связности – те же, что у исходного графа, то
есть этот подграф и будет каркасом. Можно даже точно сказать, сколько
ребер необходимо удалить для получения каркаса. Если в графе
вершин, ребер и компонент связности, то в
каркасе будет
тоже вершин и компонент связности. Но в любом
лесе с
вершинами и компонентами связности имеется
ровно 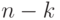n-k ребер.
Значит, удалено будет 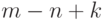m-n+k ребер. Это число называется цикломатическим
числом графа и обозначается через 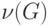nu (G) .

Если в графе есть циклы, то у него больше одного каркаса. Определить
точное число каркасов связного графа позволяет так называемая матричная
теорема Кирхгофа. Приведем ее без доказательства. Для графа
определим матрицу 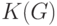K(G) – квадратную матрицу порядка с элементами

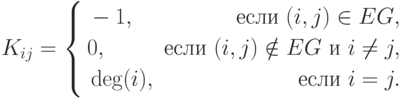
$K_{ij} =left{begin{aligned} & -1, & text{если }(i,j)in EG, \ & 0, & text {если }(i,j)notin EG t{ и } ine j,\ & deg (i), & text {если } i=j. end{aligned} right}$

Иначе говоря, 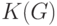K(G) получается из матрицы смежности, если
заменить
все на , а вместо нулей на главной диагонали
поставить степени вершин.
Заметим, что матрица 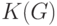K(G) – вырожденная, так как сумма
элементов
каждой строки равна , то есть столбцы линейно зависимы.

Источник

Дерево – это частный случай графа, наиболее широко применяемый в программировании.

Основные определения

Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.

Дерево – это связный граф без циклов.

Дерево – это связный граф, в котором при N вершинах всегда ровно N-1 ребро.

Дерево – это граф, между любыми двумя вершинами которого существует ровно один путь.

Аналогичным образом определяется и ориентированное дерево – как орграф, в котором между любыми двумя вершинами существует не более одного пути.

Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющей циклов.

Для каждой пары вершин дерева – узлов – существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины.

Расстояние до корневой вершины V0 называется ярусом s вершины.

Поскольку маршрут между двумя вершинами единственный, то , применяя это свойство к смежным вершинам, можно заключить, что любая ветвь является мостом.

При удалении ребра единственный маршрут прерывается и граф распадается на два подграфа.

Корневое дерево – это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:

из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;

в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.

Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья “растут” вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья – самыми нижними.

Предок вершины v – это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v – это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.

Бинарное дерево – это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.

Высота корневого дерева – это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота – это просто расстояние от корня до самого удаленного листа.

Свойства деревьев.

Граф G(V,X) является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:

1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.

2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.

3. Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.

4. Граф G(V,X) связен и не содержит циклов.

5. Граф G(V,X) связный , но утрачивает это свойство после удаления любого ребра.

Итак, дерево с n вершинами имеет n-1 ребро, поэтому оно будет минимальным связным графом.

Висячие вершины, за исключением корневой, называют листьями.

Остовом связного графа называется любой его подграф , содержащий все вершины графа и являющийся деревом.

Подграф G1 = (V1, E1) графа G = (V, E), называется остовным деревом в

графе G = (V, E), если G1 = (V1, E1) — дерево и V1 = V.

Источник