К какой группе свойств относится параметр модуль одностороннего сжатия

Упругость характеризует свойство пород восстанавливать свои первоначальные форму и объем после прекращения действия внешних нагрузок. Она характеризуется пределом упругости — максимальным значением сжимающего или растягивающего напряжения, при достижении которого порода деформируется упруго, а при превышении появляются остаточные деформации. Горные породы, необратимо изменяющие свою форму и объем под действием внешних сил без разрушения, относят к пластичным.
Восстановление формы и линейных размеров породы после снятия нагрузки происходит при их склонности к упругой деформации. Предел упругости породы — минимальные напряжения, при которых перестают проявляться упругие деформации и начинаются пластические. Модуль упругости или коэффициент пропорциональности Е между действующим нормальным напряжением а и соответствующей ему относительной продольной упругой деформацией е называют модулем продольной упругости — модулем Юнга:
Для твердых пород модуль упругости изменяется в пределах 5 -109 —1,5 – Ю11
Отношение между отдельными деформациями: продольными и поперечными называют коэффициентом поперечной деформации — коэффициентом Пуассона ц:
Для твердых пород коэффициент Пуассона изменяется в пределах 0,10-0,40.
Отношение касательного напряжения т, приложенного к образцу породы, и деформации сдвига у характеризуется модулем сдвига G:
Модули продольной упругости Е и сдвига G соответствуют описанию напряженно-деформированного состояния породы и считаются основными характеристиками упругости пород.
Хрупкость — свойство пород разрушаться под нагрузкой без пластических деформаций.
Вязкость характеризует свойство пород оказывать сопротивление при перемещении одной части относительно другой (внутреннее трение). Вязкость зависит от состава и структуры породы, формы и размера частиц, состава и количества цементирующего вещества и содержания влаги. Чем выше вязкость, тем труднее разрушить породу.
Прочность пород на сжатие, растяжение или сдвиг характеризуется пределом прочности, представляющим критическое значение сжимающего (растягивающего, сдвигающего) напряжения, при котором порода разрушается. Прочность пород или сопротивление растяжению, сжатию и сдвигу изменяется в широких пределах: на сжатие — 0,1-400 МПа, на сдвиг — 0,01—70 МПа, на растяжение — 0—40 МПа. Прочность пород характеризуется паспортом пород (рис. 1.7 а, б).
Модуль упругости — коэффициент пропорциональности между вертикальным давлением на грунт и его относительной вертикальной деформацией. Нормальное напряжение в породе:
где Е — модуль упругости, Па; 8 — относительная продольная деформация, равная А1/1 (А/ — абсолютная деформация образца породы, м; / — длина образца породы, м).
Модуль сдвига — это коэффициент пропорциональности между касательным напряжением и деформацией сдвига. Касательное напряжение:
где G — модуль сдвига, Па; v — относительная деформация породы при сдвиге.
Рис. 1.7. Схема разрушения образца (а) и диаграмма Мора для трехосных испытаний (б)
Предельное касательное напряжение, при котором происходит разрушение породы, в зависимости от действующих нормальных напряжений выражается формулой
где ср — угол наклона прямой, касательной к полуокружностям, равный пределам прочности породы на сжатие и растяжение; с — сцепление породы.
Угол (р называется углом внутреннего трения, a tg ф — коэффициентом внутреннего трения, т.е. коэффициентом пропорциональности между разрушающими касательными и нормальными напряжениями.
Сцепление породы численно равно пределу ее прочности на срез при отсутствии нормальных напряжений (когда ан = 0). Для рыхлых пород с = 0, зависимость примет вид
Угол ф характеризует угол естественного откоса рыхлых пород.
Коэффициент Пуассона является безразмерной величиной, связывающей относительную продольную и поперечную деформации горной породы:
где а — относительная поперечная деформация, равная Ad/d (Ad — абсолютная поперечная деформация породы, u,d— поперечный размер образца породы, м).
Модуль всестороннего сжатия — это коэффициент пропорциональности между напряжением и относительным изменением объема AV/V при объемном напряжении породы:
где а() — напряжение в породе при объемном напряженном состоянии, Па; к — модуль всестороннего сжатия, равный EG/3x(G – Е), Па; AV— абсолютная деформация объема породы, м3; V— первоначальный объем породы, подвергающийся деформации, м3.
Модуль одностороннего сжатия, т. е. коэффициент пропорциональности между продольным напряжением и продольной относительной деформацией при расположении рыхлой породы в цилиндре с жесткими стенками. Через модуль Юнга и коэффициент Пуассона он выражается в следующем виде:
К динамическим характеристикам горных пород относят скорость распространения продольных и поперечных волн, акустическую жесткость, динамические модули: упругости и сдвига.
Скорость продольной волны в скальных породах составляет от 2000 до 7000 м/с:
где к — модуль всестороннего сжатия, Па; р — плотность породы, кг/м3.
Скорость поперечной волны:
По скорости vM, vCT и плотности породы вычисляют динамические характеристики упругих свойств горной породы:
где
— соответственно динамические модули упругости,
всестороннего сжатия и сдвига.
По поверхности пород при динамической нагрузке распространяется поверхностная волна (волна Рэлея). Скорости распространения волн образуют ряд:
Акустическая жесткость — удельное акустическое сопротивление пород, представляющее произведение плотности породы на скорость продольной волны:
зо
Физические свойства относятся к образцам горных пород. В массиве пород из-за их трещиноватости, плоскостей ослабления, влажности показатели физических свойств ниже. Так, предел прочности массива из-за наличия макронарушений в десятки раз меньше предела прочности, определенного на образце.
Снижение сцепления в массиве по сравнению со сцеплением в образце:
где см — сцепление куска породы при отрыве от массива, Па; с0 — сцепление в куске породы, Па; к — коэффициент структурного ослабления.
Предел прочности массива на сжатие:
где асж — предел прочности на сжатие рассматриваемого участка массива, имеющего линейный размер dM (м) и модуль упругости Ем (Па); асж0 — предел прочности породы на сжатие (Па), определенный на образце, имеющем линейный размер dQ (м) и модуль упругости Е0 (Па).
Пластичность пород. В отличие от упругих деформаций пластические деформации сопровождаются необратимыми изменениями внутреннего строения породы. К последним относят сдвиговые деформации зерен, диффузионное перемещение вещества в кристаллической решетке и т.п.
Пластические деформации проявляются в горных породах при воздействии нагрузок, причем со временем они возрастают.
Пластические свойства пород проявляются в увеличении скорости роста деформаций с повышением нагрузки. В твердых горных породах пластичность объясняется сдвигом зерен по определенным плоскостям под действием напряжений. Эти деформации происходят без нарушения сплошности вещества, участвуя в проявлении остаточной несущей способности разрушенных (дискретных) пород в окрестностях горных выработок. В результате происходит взаимное перемещение, смятие по контактам, обжатие, самозаклинивание и иные физические процессы, объединяемые понятием квазипластичности, поскольку эти явления не совпадают с понятием пластичности, существующим в физике твердого тела.
Пластичность горных пород зависит от их минерального состава: жесткость частиц снижает пластичность, и наоборот, например малопластичен кварц и пластичен базальт.
Реологические свойства характеризуют изменение поведения пород при длительном воздействии нагрузок менее разрушающих, которые превышают предел упругости.
Ползучестью называют медленное нарастание пластических деформаций во времени при постоянном воздействии. Причина ползучести заключается в росте деформаций за счет скольжения и перемещения зерен пород.
Релаксацией называют явление, обратное ползучести, или снятие напряжений при постоянной деформации. Ползучесть и релаксация — проявление одного и того же реологического процесса. Если порода не потеряла способности к деформированию — имеет место ползучесть, в противном случае — релаксация. При релаксации возникшие упругие деформации переходят в пластические. Оценка реологических свойств пород важна при назначении размеров целиков и параметров крепи для учета фактора времени при практических расчетах.
Источник
При ведении буровзрывных работ (БВР) на горных предприятиях, выбор их основных параметров и методов управления взрывом, в значительной степени, зависит от свойств горных пород, трещиноватости массива и структурных особенностей его залегания. При составлении расчетов используются физические, механические, горно-технологические свойства горных пород.
Физические свойства горных пород. Физические свойства характеризуются плотностью, пористостью и пластичностью горных пород.
Плотность пород – физическая величина, равная отношению массы породы к их объему определяется по формуле:
(г/см3)
где m – масса породы, г;
V – объем породы, см3;
Пористость породы – физическая величина, равная отношению всех пустот к общему объему породы в сухом состоянии определяется по формуле:
где Vп – объем всех пустот;
Пористость породы характеризуется коэффициентом пористости.
Коэффициенты пористости некоторых типов горных пород:
Гранит, габбро, кварцит 0,8-1,2
Известняк, мрамор, доломит 0,5-13,4
Песчаник, глинистый сланец, 4-28,3
Глина, суглинок, почва 44-65
Пластичность горных пород – физические свойства горных пород сохраняют остаточную деформацию после прекращения действия внешних сил.
Влажность горных пород характеризует содержание воды в породе. Коэффициент влажности (относительная влажность) определяется по формуле:
где w – влажность приходящейся на 1г абсолютно сухой породы.
Механические свойства горных пород. К механическим свойствам горных пород, относятся предел прочности горных пород одноосному сжатию, растяжению, модуль Юнга, модуль сдвига, коэффициент Пуассона.
Предел прочности горных пород одноосному сжатию– отношение максимальной разрушающей силы при одноосном раздавливании на начальную площадь поперечного сечения образца и определяется по формуле:
где Рсж.max – максимальная сжимающая, разрушающая сила, в кг;
F0 – площадь поперечного сечения образца породы, см2;
Предел прочности горных пород одноосному растяжению – отношение максимальной разрушающей силы при одноосном растяжении на начальную площадь поперечного сечения образца определяется по формуле:
где Рр.max – максимальная растягивающая разрушающая сила, в кг;
Модуль Юнга (модуль упругости) – называется коэффициент пропорциональности между нормальным напряжением и деформацией, который определяется по формуле:
где s – нормальное напряжение, кгс/см2;
n – относительная деформация
Модуль сдвига – называется коэффициент пропорциональности между касательным напряжением и деформацией, который определяется по формуле:
где t – касательное напряжение, кгс/см2.
Коэффициент Пуассона – называют коэффициентом пропорциональности относительных продольных и поперечных деформаций.
К горно-технологическим характеристикам и классификациям горных пород относятся: крепость, твердость, абразивность, буримость, взрываемость и трещиноватость.
Крепость горных пород – оценивается по шкале проф.М.М.Протодьяконова, которая равна отношению временного сопротивления горных пород одноосного сжатия на 100 и определяется по формуле:
Твердость горных пород– это способность породы оказывать сопротивление проникновению в него твердого тела. Степень твердости для сопротивления породы при бурении определяют по методу Л.А.Шрейнера.
Абразивность горных пород – это способность породы изнашивать контактирующий с ней поверхность горных машин или горного оборудования в процессе их работы. Характеристикой абразивности горных пород оценивается по шкале Л.И.Барона и А.В.Кузнецова.
Буримость горных пород – это способность породы сопротивляться проникновению в нее бурового инструмента. Буримость породы характеризуется скоростью бурения – м/час.
Взрываемость горных пород – это сопротивляемость горной породы разрушению действием взрыва. Взрываемость характеризуется классификацией пород по взрываемости.
Трещиноватость горных пород и массивов – это совокупность трещин определенных размеров, частоты их расположения и ориентации в массиве горных пород.
Трещиноватость определяется по классификации массивов горных пород по степени их трещиноватости, которые определяются планиметрическим, фотопланиметрическим, керневым, сейсмическим и экспресс методами.
Резюме
В общем технологическом комплексе по добыче и переработке полезных ископаемых БВР, предопределяют эффективность погрузочно-транспортных работ на карьерах, а также качества дробления измельчения руд на обогатительных фабриках. Поэтому от качества буровзрывных работ зависит качество добываемой продукции.
При ведении БВР на горных предприятиях, выбор их основных параметров и методов управления взрывом, в значительной степени, зависит от физических, механических и горно-технологических свойств горного массива, а также структурных особенностей его залегания.
Источник
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела – сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
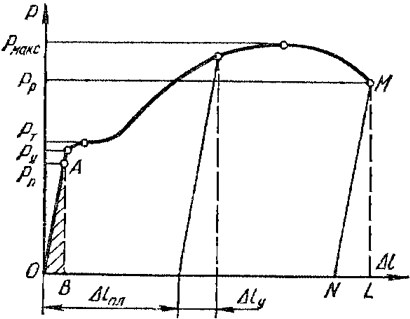
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k – коэффициент жесткости:
k = EF/l (318.2.3)
где l – длина образца, F – площадь сечения, Е – модуль Юнга.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε – отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
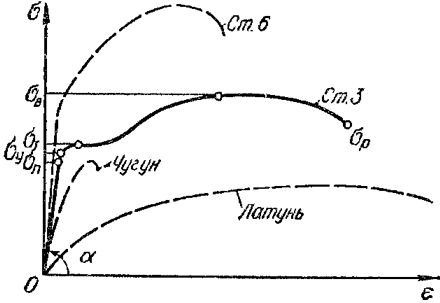
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом – углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
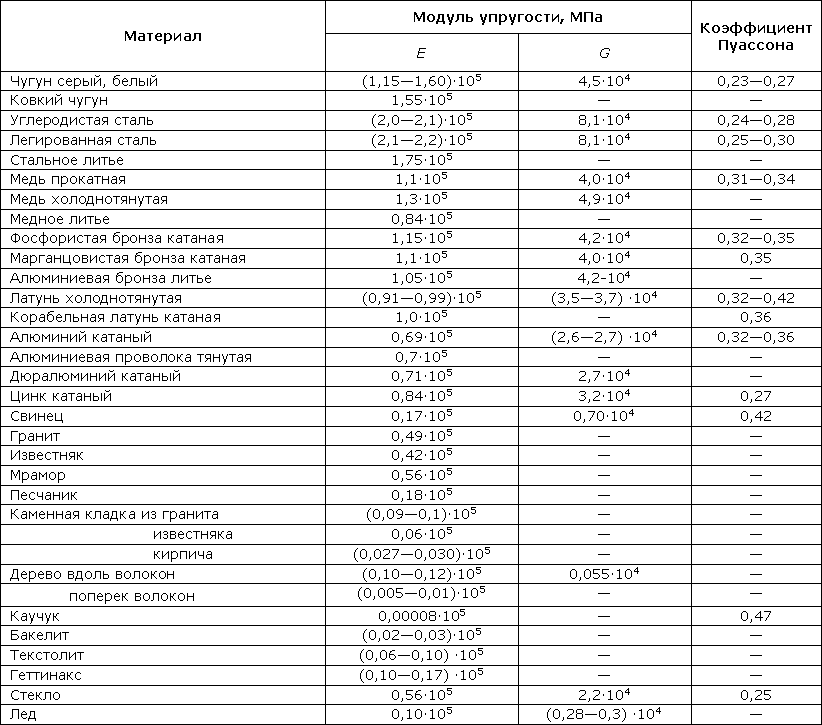
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
3. Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести – линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести – соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
В таблицах 318.2 – 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
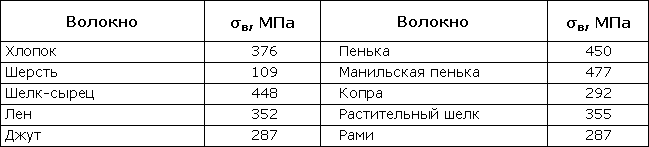
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород
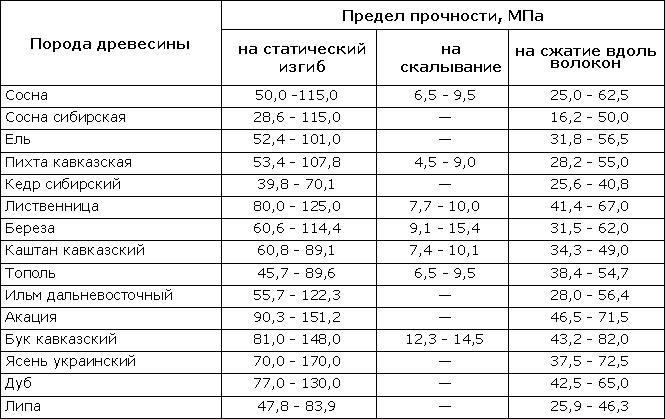
5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования “шейки” значительно изменяется площадь сечения образца в районе “шейки”. Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
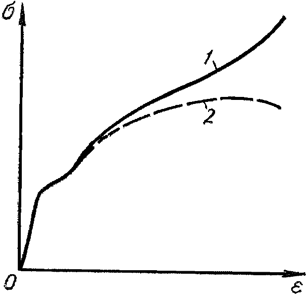
Рисунок 318.3. Диаграмма напряжений: 2 – по отношению к начальной площади поперечного сечения, 1 – по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo – F)/Fo (318.2.7)
где Fo – начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F – площадь поперечного сечения в районе “шейки”. Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 – результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η – коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5
а – для пластических материалов; б – для хрупких материалов ; в – для дерева вдоль волокон, г – для дерева поперек волокон.
Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 – 318.5.
Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.
Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.
Влияние температуры на изменение механических свойств материалов
Твердое состояние – не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.
Таблица 318.6. Температуры плавления некоторых веществ
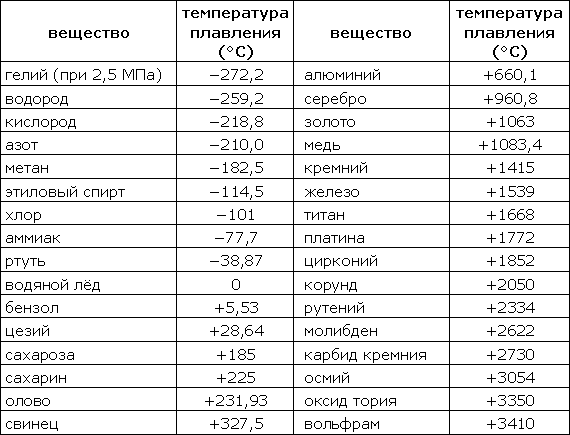
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.
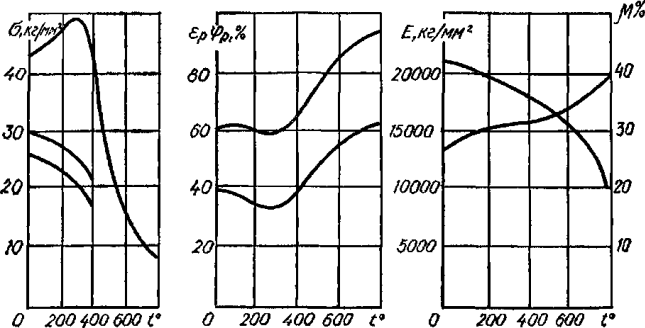
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия – увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих – повышение предела прочности (селектрон).
Источник
