Какая фигура называется ромбом свойство ромба
Определение.
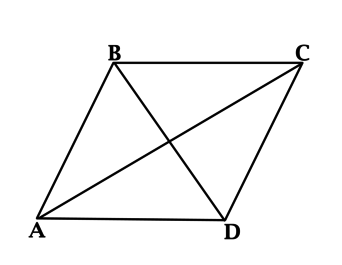
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Источник
Ðîìá – ýòî ïàðàëëåëîãðàìì ñ ðàâíûìè ñòîðîíàìè. Ðîìá ñ ïðÿìûìè óãëàìè ÿâëÿåòñÿ êâàäðàòîì.
Ðîìá ðàññìàòðèâàþò êàê âèä ïàðàëëåëîãðàììà, ñ äâóìÿ ñìåæíûìè ðàâíûìè ñòîðîíàìè ëèáî ñ âçàèìíî ïåðïåíäèêóëÿðíûìè äèàãîíàëÿìè, ëèáî ñ äèàãîíàëÿìè äåëÿùèìè óãîë íà 2 ðàâíûå ÷àñòè.

Ñâîéñòâà ðîìáà.
1. Ðîìá – ýòî ïàðàëëåëîãðàìì, ïîýòîìó ïðîòèâîïîëîæíûå ñòîðîíû èìåþò îäèíàêîâóþ äëèíó è ïàðàëëåëüíû ïîïàðíî, ÀÂ || CD, AD || ÂÑ.
2. Óãîë ïåðåñå÷åíèÿ äèàãîíàëåé ðîìáà ÿâëÿåòñÿ ïðÿìûì (AC ⊥ BD) è òî÷êîé ïåðåñå÷åíèÿ äåëÿòñÿ íà äâå îäèíàêîâûå ÷àñòè. Òî åñòü äèàãîíàëè äåëÿò ðîìá íà 4 òðåóãîëüíèêà – ïðÿìîóãîëüíûõ.
3. Äèàãîíàëè ðîìáà – ýòî áèññåêòðèñû åãî óãëîâ (∠DCA = ∠BCA, ∠ABD = ∠CBD è ò. ä.).
4. Ñóììà êâàäðàòîâ äèàãîíàëåé ðàâíÿåòñÿ êâàäðàòó ñòîðîíû, óìíîæåííîìó íà ÷åòûðå (âûâîä èç òîæäåñòâà ïàðàëëåëîãðàììà).
Ïðèçíàêè ðîìáà.
Ïàðàëëåëîãðàìì ABCD áóäåò íàçûâàòüñÿ ðîìáîì òîëüêî â ñëó÷àå âûïîëíåíèÿ õîòÿ áû îäíîãî èç óñëîâèé:
1. 2 åãî ñìåæíûå ñòîðîíû èìåþò îäèíàêîâóþ äëèíó (òî åñòü, âñå ñòîðîíû ðîìáà ðàâíû, AB=BC=CD=AD).
2. Óãîë ïåðåñå÷åíèÿ äèàãîíàëåé ïðÿìîé (AC⊥BD).
3. 1-íà èç äèàãîíàëåé äåëèò óãëû, êîòîðûå åå ñîäåðæàò ïîïîëàì.
Ïóñòü ìû çàðàíåå íå çíàåì, ÷òî ÷åòûð¸õóãîëüíèê îêàçûâàåòñÿ ïàðàëëåëîãðàììîì, îäíàêî èçâåñòíî, ÷òî âñå åãî ñòîðîíû ðàâíû. Çíà÷èò ýòîò ÷åòûð¸õóãîëüíèê ÿâëÿåòñÿ ðîìáîì.
Ñèììåòðèÿ ðîìáà.
Ðîìá ñèììåòðè÷åí îòíîñèòåëüíî âñåõ ñâîèõ äèàãîíàëåé, çà÷àñòóþ åãî èñïîëüçóþò â îðíàìåíòàõ è ïàðêåòàõ.
Ïåðèìåòð ðîìáà.
Ïåðèìåòð ãåîìåòðè÷åñêîé ôèãóðû – ñóììàðíàÿ äëèíà ãðàíèö ïëîñêîé ãåîìåòðè÷åñêîé ôèãóðû. Ó ïåðèìåòðà òà æå ðàçìåðíîñòü âåëè÷èí, ÷òî è ó äëèíû.
Ïåðèìåòð ðîìáà ðàâíÿåòñÿ ñóììå ÷åòûðåõ äëèí åãî ñòîðîí ëèáî ïðîèçâåäåíèþ äëèíû âñÿêîé èç åãî ñòîðîíû íà 4 (ò.ê. ó ðîìáà âñå ñòîðîíû ðàâíû).
ãäå:
P – ïåðèìåòð ðîìáà;
a – äëèíà ñòîðîíû ðîìáà.
Ïëîùàäü ðîìáà.
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû – ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Источник
- KtoNaNovenkogo
- ЧАстые ВОпросы
- Вы здесь
18 июня 2020
- Ромб — это…
- Признаки
- Свойства ромба
- Периметр
- Площадь ромба
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.
Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.
Ромб — это…
А вот как звучит официальное определение ромба:
Ромб – это геометрическая фигура, которая представляет собой особый вид параллелограмма (это как ?). И у него все стороны равны.
История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.
И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.
Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.
Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.
Выглядит классический параллелограмм вот так:
Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.
В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.
Признаки ромба
Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:
- Все четыре стороны параллелограмма равны;
- Диагонали параллелограмма пересекаются под углом 90 градусов;
- Диагонали параллелограмма являются еще и биссектрисами.
И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.
Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:
На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.
Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.
Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).
Свойства ромба
А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:
- Диагонали ромба пересекаются между собой под прямым углом.
- Диагонали ромба также представляют собой и биссектрисы его углов.
И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:
Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.
Периметр ромба
Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.
В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:
Как несложно догадаться, буква «а» здесь – это длина стороны ромба.
Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.
Площадь ромба
Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.
Классическая формула для расчета площади ромба – через длины стороны и высоты.
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.
Она обозначается буквой «h» или «H» и выглядит вот так:
И наконец, формула для расчета площади ромба через сторону и высоту:
Есть и другие формулы для расчета площади ромба:
- Если известны диагонали:
- Если известны сторона и угол:
- Если известны угол и радиус вписанной окружности:
- Если известны сторона и радиус вписанной окружности:
Вот и все, что мы хотели рассказать о ромбе.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Комментарии и отзывы (1)
Со временем, разница между квадратом, ромбом и параллелограммом забывается. То, что было само собой разумеющимся в школе, теперь кажется чем-то новым!:) Кстати, во времена СССР, именно ромб был самой популярной фигурой в дизайне всевозможных логотипов.
Источник
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сумма внутренних углов любого четырехугольника равна (360^circ).
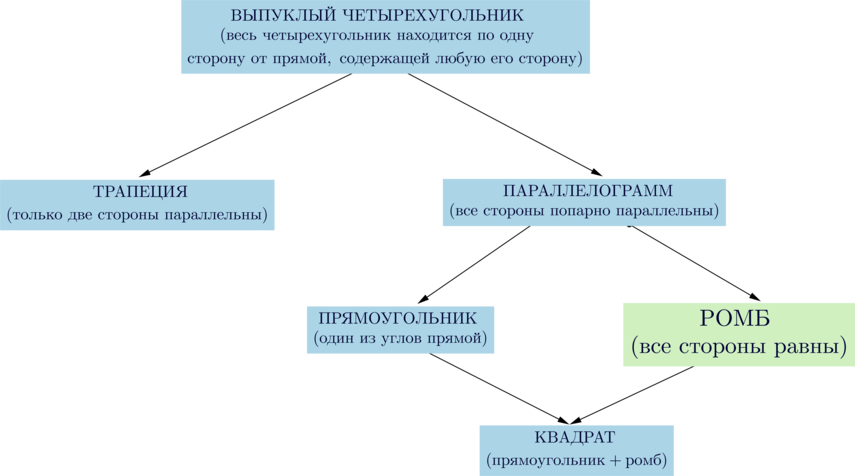
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
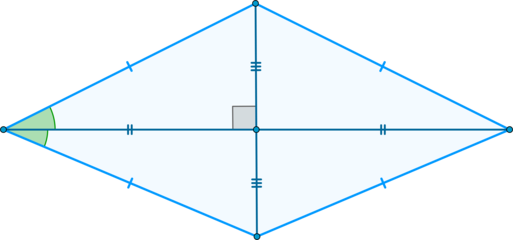
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.

В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} – angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
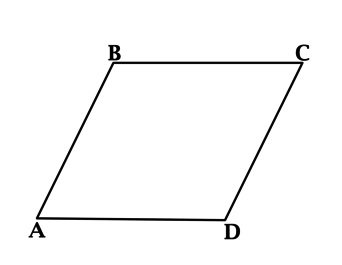
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
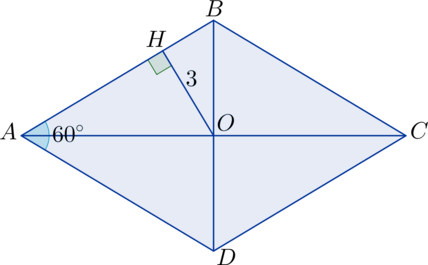
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
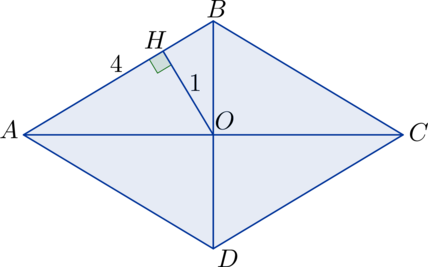
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 8).
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
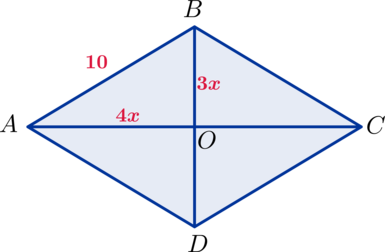
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
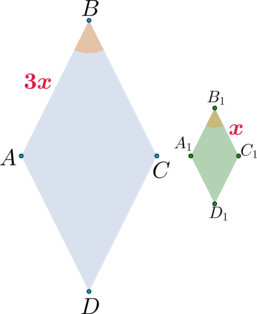
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.
Источник
