Какая функция называется степенной ее свойства и график

10 класс

СТЕПЕННАЯ ФУНКЦИЯ

Степенной называется функция, заданная формулой где , p– некоторое действительное число.

I. Показатель – чётное натуральное число. Тогда степенная функция где n – натуральное число, обладает следующими свойствами:

1) Область определения функции – множество всех действительных чисел: D(y)=(−; +).

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если :

3) ). Значит, функция является чётной, её график симметричен относительно оси Oy.

4) Если , то функция убывает при х (- ; 0] и возрастает при х [0; + ).

Если , то функция возрастает при х (- ; 0] и убывает при х [0; + ).

Графиком степенной функции с чётным натуральным показателем является парабола п-ой степени, симметричная относительно оси ординат, с вершиной в начале координат (в точке ), ветви которой направлены вверх, если , и вниз, если . График этой функции получается из графика функции растяжением вдоль оси Оу в а раз, если a > 1; и сжатием к оси Ох в а раз, если 0 < a < 1.

На левом рисунке изображены примеры графиков степенных функций с чётным натуральным показателем, а на правом рисунке – графики тех же функций, но с растяжением и сжатием.

II. Показатель – нечётное натуральное число. Тогда степенная функция где n – натуральное число, обладает следующими свойствами:

1) Область определения функции – множество всех действительных чисел: D(y)=(−; +).

2) Область значений функции – множество всех действительных чисел: Е(y) = (−; +).

3) Значит, функция является нечётной, её график симметричен относительно начала координат.

4) Если , функция возрастает при х (- ; +).

Если , функция убывает при х (- ; +).

Графиком степенной функции с нечётным натуральным показателем является парабола п-ой степенис вершиной в начале координат (точке (0;0)), симметричная относительно начала координат, ветви которой расположены в I и III четвертях, если ; и во II и IV четвертях, если . График этой функции получается из графика функции растяжением вдоль оси Оу в а раз, если a > 1; и сжатием к оси Ох в а раз, если 0 < a < 1.

На левом рисунке изображены примеры графиков степенных функций с нечётным натуральным показателем, а на правом – графики тех же функций, но с растяжением и сжатием.

III. Показатель – чётное целое отрицательное число. Тогда степенная функция где n – натуральное число, обладает следующими свойствами:

1) Область определения функции: .

2) Область значений функции – множество всех положительных чисел, если : Е(y) =(0; +);

множество всех отрицательных чисел, если : Е(y) =(-; 0).

3) Значит, функция является чётной, её график симметричен относительно оси Оу.

4) Если , функция возрастает при х (- ; 0), убывает при х (0; + ).

Если функция убывает при х (- ; 0), возрастает при х (0; + ).

Графиком степенной функции является гипербола п-ой степени, симметричная относительно оси Оу, не пересекающая оси координат и её ветви расположены в I и II четвертях, если , и в III и IV четвертях, если . График этой функции получается из графика функции растяжением вдоль оси Оу в а раз, если a > 1; и сжатием к оси Ох в а раз, если 0 < a < 1.

На первом рисунке изображены примеры графиков степенных функций с чётным целым отрицательным показателем, а на втором рисунке – графики тех же функций, но с растяжением и сжатием.

IV. Показатель – нечётное целое отрицательное число. Тогда степенная функция где n – натуральное число, обладает следующими свойствами:

1) Область определения функции:

2) Область значений функции:

3) Значит, функция является нечётной, её график симметричен относительно начала координат.

4) Если , функция убывает при х .

Если , функция возрастает при х .

Графиком степенной функции является гипербола п-ой степени, симметричная относительно начала координат, не пересекающая оси координат и его ветви расположены в I и III четвертях, если , и во II и IV четвертях, если . График этой функции получается из графика функции растяжением вдоль оси Оу в а раз, если a > 1; и сжатием к оси Ох в а раз, если 0 < a < 1.

На левом рисунке изображены примеры графиков степенных функций с нечётным целым отрицательным показателем, а на правом рисунке – графики тех же функций, но с растяжением и сжатием.

V. Показатель – положительная правильная дробь . Тогда степенная функциягде m– целое положительное число, n > 1 – натуральное число, обладает следующими свойствами:

1) Областью определения функции, исходя из определения степени с рациональным показателем, является множество неотрицательных чисел:

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если : .

3) Функция неявляется ни чётной, ни нечётной, так как её область определения не содержит противоположных значений.

4) Если , функция возрастает при х ;

Если , функция убывает при х .

График степенной функции расположен в I четверти, если , и в IV четверти, если . График этой функции получается из графика функции растяжением вдоль оси Оу в а раз, если a > 1; и сжатием к оси Ох в а раз, если 0 < a < 1.

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде положительной правильной дроби и графики тех же функций, но с растяжением и сжатием.

VI. Показатель – положительная неправильная дробь . Тогда степенная функциягде m– целое положительное число, n > 1 – натуральное число, обладает следующими свойствами:

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если : .

4) Если , функция возрастает при х ;

Если , функция убывает при х .

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде положительной неправильной дроби и графики тех же функций, но с растяжением и сжатием.

VII. Показатель – отрицательная правильная дробь . Тогда степенная функциягде m– целое отрицательное число, n > 1 – натуральное число, обладает следующими свойствами:

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если : .

4) Если , функция убывает при х ;

Если функция возрастает при х .

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде отрицательной правильной дроби и графики тех же функций, но с растяжением и сжатием.

VIII. Показатель – отрицательная неправильная дробь . Тогда степенная функциягде m– целое отрицательное число, n > 1 – натуральное число, обладает следующими свойствами:

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если : .

4) Если функция убывает при х ;

Если функция возрастает при х .

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде отрицательной неправильной дроби и графики тех же функций, но с растяжением и сжатием.

Источник

Формулы со степенной функцией

На области определения степенной функции y = x p имеют место следующие формулы:
; ;
;
; ;
; ;
; .

Свойства степенных функций и их графики

Далее мы рассматриваем степенную функцию
y(x) = x p .

Степенная функция с показателем равным нулю, p = 0

Если показатель степенной функции y = x p равен нулю, p = 0, то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице:
y = x p = x 0 = 1, x ≠ 0 .

Степенная функция с натуральным нечетным показателем, p = n = 1, 3, 5, …

Рассмотрим степенную функцию y = x p = x n с натуральным нечетным показателем степени n = 1, 3, 5, …. Такой показатель также можно записать в виде: n = 2k + 1, где k = 0, 1, 2, 3, … – целое не отрицательное. Ниже представлены свойства и графики таких функций.

График степенной функции y = x n с натуральным нечетным показателем при различных значениях показателя степени n = 1, 3, 5, ….

Область определения: –∞ < x < ∞
Множество значений: –∞ < y < ∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ < x < 0 выпукла вверх
при 0 < x < ∞ выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1,
y(–1) = (–1) n ≡ (–1) 2k+1 = –1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 1, функция является обратной к самой себе: x = y
при n ≠ 1, обратной функцией является корень степени n:

Степенная функция с натуральным четным показателем, p = n = 2, 4, 6, …

Рассмотрим степенную функцию y = x p = x n с натуральным четным показателем степени n = 2, 4, 6, …. Такой показатель также можно записать в виде: n = 2k, где k = 1, 2, 3, … – натуральное. Свойства и графики таких функций даны ниже.

График степенной функции y = x n с натуральным четным показателем при различных значениях показателя степени n = 2, 4, 6, ….

Область определения: –∞ < x < ∞
Множество значений: 0 ≤ y < ∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x ≤ 0 монотонно убывает
при x ≥ 0 монотонно возрастает
Экстремумы: минимум, x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = (–1) n ≡ (–1) 2k = 1
при x = 0, y(0) = 0 n = 0
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = 2, квадратный корень:
при n ≠ 2, корень степени n:

Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3, …

Рассмотрим степенную функцию y = x p = x n с целым отрицательным показателем степени n = -1, -2, -3, …. Если положить n = –k, где k = 1, 2, 3, … – натуральное, то ее можно представить в виде:

График степенной функции y = x n с целым отрицательным показателем при различных значениях показателя степени n = -1, -2, -3, ….

Нечетный показатель, n = -1, -3, -5, …

Ниже представлены свойства функции y = x n с нечетным отрицательным показателем n = -1, -3, -5, ….

Область определения: x ≠ 0
Множество значений: y ≠ 0
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно убывает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вверх
при x > 0: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = –1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –1,
при n < –2,

Четный показатель, n = -2, -4, -6, …

Ниже представлены свойства функции y = x n с четным отрицательным показателем n = -2, -4, -6, ….

Область определения: x ≠ 0
Множество значений: y > 0
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно возрастает
при x > 0: монотонно убывает
Экстремумы: нет
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Знак: y > 0
Пределы:
; ; ;
Частные значения:
при x = –1, y(–1) = (–1) n = 1
при x = 1, y(1) = 1 n = 1
Обратная функция:
при n = –2,
при n < –2,

Степенная функция с рациональным (дробным) показателем

Рассмотрим степенную функцию y = x p с рациональным (дробным) показателем степени , где n – целое, m > 1 – натуральное. Причем, n, m не имеют общих делителей.

Знаменатель дробного показателя – нечетный

Пусть знаменатель дробного показателя степени нечетный: m = 3, 5, 7, … . В этом случае, степенная функция x p определена как для положительных, так и для отрицательных значений аргумента x. Рассмотрим свойства таких степенных функций, когда показатель p находится в определенных пределах.

Показатель p отрицательный, p < 0

Пусть рациональный показатель степени (с нечетным знаменателем m = 3, 5, 7, … ) меньше нуля: .

Графики степенных функций с рациональным отрицательным показателем при различных значениях показателя степени , где m = 3, 5, 7, … – нечетное.

Нечетный числитель, n = -1, -3, -5, …

Приводим свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -1, -3, -5, … – нечетное отрицательное целое, m = 3, 5, 7 … – нечетное натуральное.

Четный числитель, n = -2, -4, -6, …

Свойства степенной функции y = x p с рациональным отрицательным показателем , где n = -2, -4, -6, … – четное отрицательное целое, m = 3, 5, 7 … – нечетное натуральное.

Показатель p положительный, меньше единицы, 0 < p < 1

График степенной функции с рациональным показателем (0 < p < 1) при различных значениях показателя степени , где m = 3, 5, 7, … – нечетное.

Нечетный числитель, n = 1, 3, 5, …

Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 < p < 1, где n = 1, 3, 5, … – нечетное натуральное, m = 3, 5, 7 … – нечетное натуральное.

Область определения: –∞ < x < +∞
Множество значений: –∞ < y < +∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при x < 0: выпукла вниз
при x > 0: выпукла вверх
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Знак:
при x < 0, y < 0
при x > 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Четный числитель, n = 2, 4, 6, …

Представлены свойства степенной функции y = x p с рациональным показателем , находящимся в пределах 0 < p < 1, где n = 2, 4, 6, … – четное натуральное, m = 3, 5, 7 … – нечетное натуральное.

Область определения: –∞ < x < +∞
Множество значений: 0 ≤ y < +∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0: монотонно убывает
при x > 0: монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вверх при x ≠ 0
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Знак: при x ≠ 0, y > 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Показатель p больше единицы, p > 1

График степенной функции с рациональным показателем (p > 1) при различных значениях показателя степени , где m = 3, 5, 7, … – нечетное.

Нечетный числитель, n = 5, 7, 9, …

Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 5, 7, 9, … – нечетное натуральное, m = 3, 5, 7 … – нечетное натуральное.

Область определения: –∞ < x < ∞
Множество значений: –∞ < y < ∞
Четность: нечетная, y(–x) = – y(x)
Монотонность: монотонно возрастает
Экстремумы: нет
Выпуклость:
при –∞ < x < 0 выпукла вверх
при 0 < x < ∞ выпукла вниз
Точки перегибов: x = 0, y = 0
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = –1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Четный числитель, n = 4, 6, 8, …

Свойства степенной функции y = x p с рациональным показателем, большим единицы: . Где n = 4, 6, 8, … – четное натуральное, m = 3, 5, 7 … – нечетное натуральное.

Область определения: –∞ < x < ∞
Множество значений: 0 ≤ y < ∞
Четность: четная, y(–x) = y(x)
Монотонность:
при x < 0 монотонно убывает
при x > 0 монотонно возрастает
Экстремумы: минимум при x = 0, y = 0
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
;
Частные значения:
при x = –1, y(–1) = 1
при x = 0, y(0) = 0
при x = 1, y(1) = 1
Обратная функция:

Знаменатель дробного показателя – четный

Пусть знаменатель дробного показателя степени четный: m = 2, 4, 6, … . В этом случае, степенная функция x p не определена для отрицательных значений аргумента. Ее свойства совпадают со свойствами степенной функции с иррациональным показателем (см. следующий раздел).

Степенная функция с иррациональным показателем

Рассмотрим степенную функцию y = x p с иррациональным показателем степени p. Свойства таких функций отличаются от рассмотренных выше тем, что они не определены для отрицательных значений аргумента x. Для положительных значений аргумента, свойства зависят только от величины показателя степени p и не зависят от того, является ли p целым, рациональным или иррациональным.

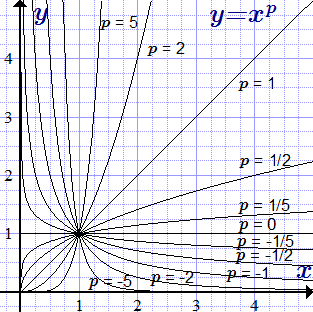Графики степенной функции y = x p при различных значениях показателя p.

Степенная функция с отрицательным показателем p < 0

Область определения: x > 0
Множество значений: y > 0
Монотонность: монотонно убывает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: нет
Пределы: ;
Частное значение: При x = 1, y(1) = 1p = 1

Степенная функция с положительным показателем p > 0

Показатель меньше единицы 0 < p < 1

Область определения: x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вверх
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0.
При x = 1, y(1) = 1 p = 1

Показатель больше единицы p > 1

Область определения: x ≥ 0
Множество значений: y ≥ 0
Монотонность: монотонно возрастает
Выпуклость: выпукла вниз
Точки перегибов: нет
Точки пересечения с осями координат: x = 0, y = 0
Пределы:
Частные значения: При x = 0, y(0) = 0 p = 0.
При x = 1, y(1) = 1 p = 1

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 12-08-2014 Изменено: 14-12-2018

Источник

Инфоурок
›

Другое
›Презентации›Степенная функция. Её свойства и график

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Степенная функция
Её свойства и график
Работа ученика
10«Б» класса
Медведева Сергея

2 слайд

Описание слайда:

у = х2
х
у
у = х3
х
у
х
у
Парабола
Кубическая
парабола
Гипербола
у = х
х
у
Прямая
Частные случаи степенной функции

3 слайд

Описание слайда:

Функция вида у = хр, где р – действительное число называется степенной функцией
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень

4 слайд

Описание слайда:

Показатель р = 2n – четное натуральное число
1

х
у
у = х2, у = х4 , у = х6, у = х8, …
у = х2
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на

промежутке
Функция возрастает

на промежутке

5 слайд

Описание слайда:

y
x
-1 0 1
у = х2
у = х6

6 слайд

Описание слайда:

Показатель р = 2n-1 – нечетное натуральное число
1
х
у
у = х3, у = х5, у = х7, у = х9, …
у = х3
Функция у=х2n-1 нечетная,
т.к. (–х)2n-1 = – х2n-1

Функция возрастает на промежутке

7 слайд

Описание слайда:

y
x
-1 0 1
у = х3
у = х7

8 слайд

Описание слайда:

Показатель р = – 2n, где n – натуральное число
1

х
у
у = х-2, у = х-4 , у = х-6, у = х-8, …
Функция у=х2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на

промежутке
Функция убывает

на промежутке

9 слайд

Описание слайда:

y
x
-1 0 1
у = х-2
у = х-6

10 слайд

Описание слайда:

Функция убывает

на промежутке
Показатель р = – (2n-1), где n – натуральное число
1

х
у
у = х-3, у = х-5 , у = х-7, у = х-9, …
Функция у=х-(2n-1) нечетная,
т.к. (–х)–(2n-1) = –х–(2n-1)
Функция убывает на

промежутке

11 слайд