Какие бывают математические свойства

Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
Дорогие друзья! Сегодня на странице своего канала я размещаю публикацию своего друга, математика, специалиста в области проективной геометрии Франца Германа. Его работы очень помогли мне в постижении многих премудростей геометрической науки. Всем, кто серьёзно думает заняться вопросами Пространства, я рекомендую ознакомиться с его публикациями на его личном сайте. Франц живёт и работает в Германии, серьёзно увлекается футболом и квантовой физикой элементарных частиц. И хотя наши взгляды на разные темы не всегда совпадают, я с уважением отношусь к любой его точке зрения. Итак.
Основное свойство математики
Спросите у своих знакомых, знают ли они основное свойство математики. Скорее всего, если вы не профессиональный математик, то ответ будет отрицательным. А какие вообще свойства присущи этой науке? Кто-то скажет, что математика непонятна. А для кого-то математика является интересной. Кто-то скажет, что она таинственна, кто-то увидет в ней поэзию… Лейбниц назвал еѐ «музыкой души». Гильберт сравнил огромным садом. Сколько людей вы спросите, столько ответов и получите. Так всѐ-таки существует ли основное свойство математики и как оно звучит? На этот вопрос ответят лучше всего наверное сами математики. Математика – это научное чудо. Одно из главных свойств математики в том, что она призвана помогать другим наукам. Карл Маркс говорил, что «наука только тогда достигает совершенства, когда ей удаѐтся пользоваться математикой». Возможно математика является хранительницей истины в последней инстанции. А ведь математика создана, как и вся наука, человеческим разумом. А. Н. Колмогоров, например, так определяет математику: «математика – это то, посредством чего люди управляют природой и собой». Не будем томить неискушѐнного читателя. Учѐные пришли к выводу, что основное свойство математики проявляется в том, что математика почему-то описывает законы природы и «…точность этих законов, если над ней задуматься, обладает всеми элементами чуда». Эти слова принадлежат выдающемуся физику-теоретику, лауреату Нобелевской премии Е. Вигнеру. Наверно, один из первых, кто обратил на это математическое свойство внимание, был выдающийся итальянский учѐный Галилей, когда в конце шестнадцатого века сбрасывал шары различной массы с Пизанской башни и открыл закон свободного падения: скорость падающего тела пропорциональна времени падения и не зависит от его массы (Аристотель был не прав). Спустя чуть больше полувека Ньютон открыл свой знаменитый закон всемирного тяготения. Примерно в это же время, используя огромный архив астрономических наблюдений, Кеплер открыл законы движения небесных тел, а Ньютон показал, что эти законы выводятся чисто математически. Наверное с этого времени и началось победное шествие главного математического свойства. Учѐные физики стали описывать законы природы на языке математики. Планета Уран была открыта «на кончике пера». Были рассчитаны параметры орбиты Урана, а чуть позже астрономы увидели еѐ визуально в телескоп. Великий английский учѐный Фарадей был самоучкой. Он описывал все свои опыты с электричеством словесно, без единой математической формулы. Он просто не знал математики. Однако, чуть позже не менее великий его соотечественник Дж. Максвелл, когда познакомился с трудами Фарадея, понял, что опыты эти очень хорошо описываются математикой. Так родилась электродинамика и открыла собой эру теоретической физики. Теоретическая физика – это наука, инструментом которой и является математика. А на основе еѐ построений физики-экспериментаторы проверяют на своих опытах построения теоретиков. Сегодня физические эксперименты с невероятной точностью подтверждают математические расчѐты теоретиков. Например, в квантовой электродинамике такая точность доходит аж до одиннадцатого знака после запятой. В настоящее время всѐ естествознание буквально пронизано математикой. Более того экономические науки, биология, медицина невозможны сегодня без математики. Компьютеризация и нанотехнологии с их невообразимыми по сложности коллайдерами и космическими аппаратами основаны на фундаментальных принципах математической науки. В общем вся современная деятельность человечества невозможна без математики. Но давайте заглянем и в саму математику. Любая математическая теория является более фундаментальной, чем меньше аксиом требуется для еѐ определения. В математике такой теорией является теория групп. Для еѐ определения требуется всего четыре аксиомы. Сегодня ни одно направление в математике не может обойтись без теории групп. При помощи теории групп строятся новые геометрии, о чѐм математики прошлого не могли даже и мечтать. Любой математический аппарат, где используется современная топология, не может обойтись без теории групп. Теорию групп порой называют теорией симметрии. Методы теории групп используются не только в самой математике, но и в других науках. Например, в квантовой механике и физике элементарных частиц, современной кристаллографии и такой абстрактной науке, как общая теория систем. Теория групп – это любимое детище математиков ХХ века и современности. Однако, вернѐмся к основному свойству математики – почему законы природы описываются с невероятной точностью математикой? Мне представляется такая схема (Рис. 1).
Природа – (П) – по каким-то законам, отвечающим самым глубоким и фундаментальным законам математики – (М) – создала человеческий разум – (Р):
Разум, постигая природу, создаёт мощнейший инструмент познания – математику:
Математика, движимая разумом помогает понять тайны природы:
Цикл замкнулся. Мне кажется, что в этом и есть суть вечного развития и познания природы, познания истины.
Можно подвести итог: МИР САМОВОЗНИК И САМОРАЗВИВАЕТСЯ ПО ЗАКОНАМ МАТЕМАТИКИ.
Но будущих Лобачевских, Ньютонов и Эйнштейнов ещё ждёт множество научных открытий. Ещё не создана теория вселенского разума (ТВР), ещё не открыты фундаментальные теоремы и уравнения ТВР.
Ф. Герман.
Всего Вам доброго.
Источник
Математика — царица наук. Математика любит порядок. Поэтому в математике существуют много законов (свойств). Хотите узнать о некоторых из них? Зная математические законы, вы будете легко путешествовать по стране числе…
Свойства сложения
Переместительное свойство сложения
Посмотрите на яблоню…
С яблони упали яблоки… Может быть сначала упали 2 яблока, а потом 4. А может быть сначала упали 4 яблока, а потом 2? В любом случае на земле одинаковое количество яблок. Верно?
2 + 4 = 6 ИЛИ 4 + 2 = 6
Суммы «2 + 4» и «4 + 2» равны, то есть, 2 + 4 = 4 + 2 . Их записи отличаются тем, что в них переставлены местами слагаемые…. Это первый математический закон (или свойство)!
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так: a + b = b + a
Если мама тебя отправила в супермаркет и попросила купить молоко и хлеб.

Есть разница, если ты сначала пойдешь в супермаркете за хлебом, а потом в молочный отдел за молоком? Или сначала пойдешь за молоком, а потом пойдешь за хлебом? …. Верно, разницы нет. Результат одинаковый — ты купишь молоко и хлеб.

Сочетательное свойство сложения
Итак, Мама решила испечь торт. Попросила тебя купить продуктов в супермаркете и дала список продуктов, которые нужно купить…

 Рассмотрим два варианта. 1 вариант. Сначала ты пойдешь в кондитерский отдел и положишь в корзину 1 шоколадку, потом отправишь в отдел «Овощи и фрукты» …
Рассмотрим два варианта. 1 вариант. Сначала ты пойдешь в кондитерский отдел и положишь в корзину 1 шоколадку, потом отправишь в отдел «Овощи и фрукты» …

То есть 1 + (2 + 4)
Или…

2 вариант. Сначала в отделе «Овощи и фрукты» ты купишь 4 яблока и 2 банана, а потом пойдешь за шоколадкой. То есть (4 + 2) + 1.
Сколько продуктов у тебя окажется в корзине????
Правильно!!!! И в первом случае, и во втором случае продуктов в корзине ОДИНАКОВОЕ- 7!
Это СОЧЕТАТЕЛЬНОЕ свойство сложения!!!! При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Чтобы прибавить к числу сумму двух чисел, можно к этому числу прибавить первое слагаемое суммы и к полученному результату прибавить второе слагаемое суммы.
В буквенном виде: (a + b) + c = a + (b + c)

Тренируйся ….
1. Вычисли сумму слагаемых по-разному:
а) 5 + 3 + 5 б) 7 + 8 + 13 в) 24 + 9 + 16
2. Вычислите результаты выражений:
а) 19 + 4 + 16 + 1 б) 8 + 15 + 12 + 5 в) 20 + 9 + 30 + 1
3. Вычислите сумму удобным способом:
а) 10 + 12 + 8 + 20 б) 17 + 4 + 3 + 16 в) 9 + 7 + 21 + 13
Свойства вычитания
Свойство вычитания суммы из числа
Ты нашёл в супермаркете всё, что сказала мама и отправляешься к кассе….

Мама тебе дала 100 рублей…
Пока ты стоял в очереди к кассе, ты посчитал ( ты же умный ребёнок), что надо заплатить 80 рублей.
Ура! Значит останется сдача в 20рублей! (100 рублей — 80 рублей = 20 рублей)
А это значит, можно купить твою любимую жевательную резинку, которая стоит 10 рублей! (надо учесть, что мама разрешает тебе на сдачу что-то покупать….)!!!!
Подходит твоя очередь Рассмотрим два варианта.
1 вариант. Кассир посчитала все покупки: и для мамы и твою покупку (жевательную резинку) и вычла из 100 рублей.
100 — (80+10)
2 вариант. Кассир вычла из 100 рублей сначала покупки для мамы, а потом твою жевательную резинку.
100 — 80 — 10
Сколько сдачи даст кассир в 1 варианте? А сколько во 2 варианте?
Верно!!! ОДИНАКОВО! И в 1 варианте и во 2 варианте сдача будет 10 рублей!
Это один из математических законов вычитания….
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем вычесть другое слагаемое.
a − (b + c) = a − b − c
или
a − (b + c) = (a − с) − b
Благодаря этому свойству можно намного удобнее решать выражения:
128 — (28 + 6)= 128 — 28 -6 = 100 — 6 = 94
949 — ( 8 + 49) = 949 — 49 — 8 = 900 -8 = 892
Попробуй сам/а:

Свойство вычитания числа из суммы
Так…. по дороге домой из супермаркета ты встретил свою одноклассницу, которая почему — то была в плохом настроении. 
Ты вспомнил, что у тебя в карманах лежат ириски. В одном кармане — 1 ириска, а во втором — 2 ириски. Ты решаешь сделать благородный поступок — угостить одноклассницу ириской, чтобы поднять ей настроение (к тому же она тебе нравится….)
Рассмотрим два варианта. 1 вариант. Ты достаешь ириску из первого кармана. Второй вариант — ты достаешь ириску из второго кармана.
Вопрос. Сколько ирисок у тебя останется? …. Правильно!!!!! И в 1 и во 2 варианте останется 2 ириски.
Это ещё одно математическое свойство….
.Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) − c = (a − c) + b (если a > c или а = с)
или
(a + b) − c = (b − c) + a (если b > c или b = с)
Это свойство. Этот математический закон может пригодиться для рационального (удобного) способа решения выражений
(73 + 59) — 73 = (73 — 73) + 59 = 0 + 59 = 59
(345 + 217) — 245 = (345 — 245) + 217 = 100 + 217 = 317
Потренируйся и ты…

Памятка…

Источник
Мы каждый день сталкиваемся с большим количеством одинаковых предметов, но не задумываемся о том, как называется совокупность этих объектов. Это множество – математическая единица, подчиняющаяся определенным законам и правилам, обладающая разными свойствами и функциями.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками { }.
Пример:
А = {а, в, с, у} – А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N = {a, b, c, y}, а Є N – элемент «а» принадлежит N.
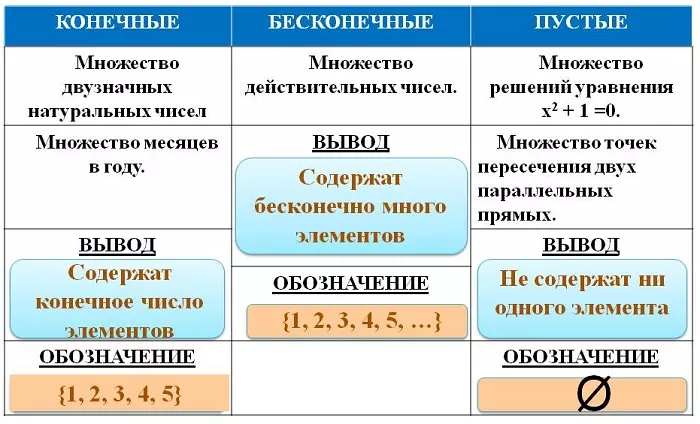
Выделяют три вида множеств:
конечные – совокупности, имеющие максимальный и минимальный предел (например, отрезок);
бесконечные – не являющиеся конечными (например, числовые);
пустые (обозначаются Ø) – не имеющие элементов.
Если две разные совокупности содержат одинаковые элементы, то одна из них (со всеми своими элементами) является подмножеством другой и обозначается знаком – ⊆.
Пример: А = {а, в, с, у} и В = {а, в, с, е, к} – все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
К совокупности натуральных чисел (N) относятся цифры, используемые при счете – от 1 до бесконечности.

Натуральные числа используют для исчисления порядка предметов. Обязательное условие данной числовой группы – каждое следующее число больше предыдущего на единицу.
N = {9, 11, 13, 15……}.
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Z = {-112, -60, -25, 0, 36, 58, 256}.
Следовательно, N – подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.
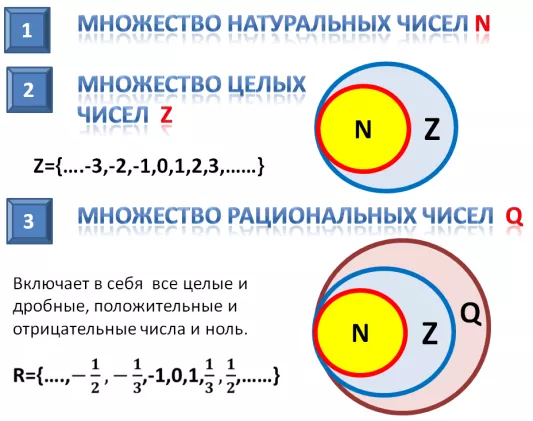
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Q={-½; 0; ½, 5; 10}.
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
5 = 5/1 = 10/2 = 25/5;
0,45 = 45/100 = 9/20.
Следовательно, N и Z являются подмножествами Q.
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
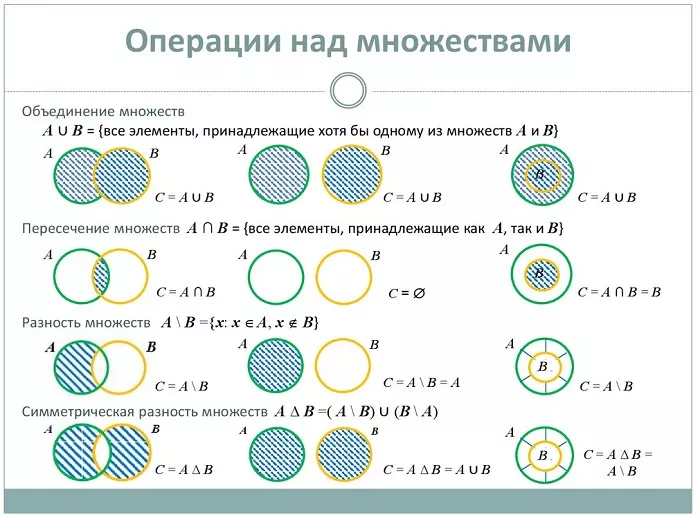
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Пример: В = {1, 6, 17} и С = {2, 13, 18}, В ∪ С= {1, 2, 6, 13, 17, 18}.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Пример: В = {36, 42, 53, 64} и С = {32, 42, 55, 66}, В ∩ С = {42}.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
Пример: В = {12, 14, 16, 18} и С = {13, 14, 15, 17}, В / С = {14}.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
Транзитивность – законы включения:
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
S ∩ S = S;
S ∪ S = S.
О других свойствах операций можно узнать из картинки:

Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
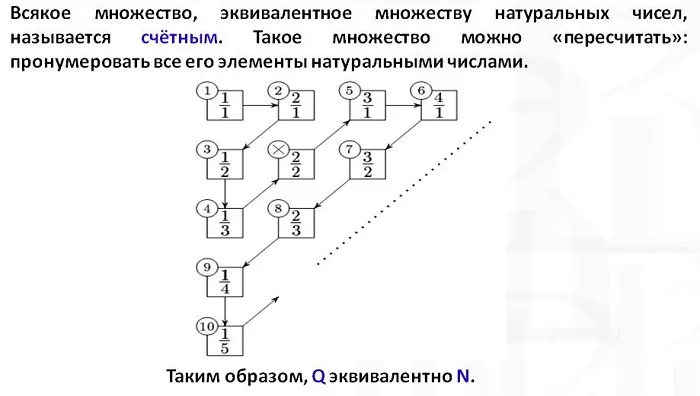
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
В случае, когда бесконечное множество равномощно натуральному ряду чисел, оно называется счетным, а если оно не равномощно – несчетным. Другими словами, счетная единица – это совокупность, которую мы можем представить в виде последовательности чисел по порядковым номерам.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
Теория множеств – достаточно широкая тема, которая требует глубокого изучения. Она затрагивает начальный курс математики, изучается в среднем звене школьной программы по алгебре. Высшая математика, математический анализ, логика – рассматривают законы, теоремы, аксиомы множеств, на которых основаны фундаментальные знания науки.
Источник
