Какие бывают свойства умножения и деления
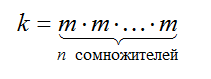
- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
- Свойства умножения
1) Переместительное свойство: от перестановки множителей произведение не изменится.
3 • 4 = 12
4 • 3 = 12
Значит, 3 • 4 = 4 • 3
2) Сочетательное свойство: два соседних множителя можно заменить их произведением.
(6 • 2) • 5 = 6 • (2 • 5)
3) Распределительное свойство: при умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
(3 + 10) • 7 = 3 • 7 + 10 • 7 = 91.
4) Чтобы умножить сумму на число, можно сначала выполнить сложение и полученный результат умножить на число:
(3 + 10) • 7 = 13 • 7 = 91.
5) Чтобы умножить число на произведение, можно сначала выполнить умножение в скобках, а затем умножить число на полученный результат:
4 • (3 • 5) = 4 • 15 = 60.
6) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат:
2 • (3 + 5) = 2 • 8 = 16
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Умножение
Правило встречается в следующих упражнениях:
3 класс
Страница 46. Вариант 1. Проверочная работа 1,
Моро, Волкова, Проверочные работы
Страница 47. Вариант 2. Проверочная работа 1,
Моро, Волкова, Проверочные работы
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 101,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
4 класс
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 17,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 24,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 42,
Моро, Волкова, Рабочая тетрадь, часть 2
Источник
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a – b) = m · a – m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a – b) · m = a · m – b · m.
Переход от умножения:
m · (a + b) и m · (a – b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a – m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a – m · b
к умножению:
m · (a + b) и m · (a – b)
называется вынесением общего множителя за скобки.
Источник
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
Умножение натуральных чисел
Результат умножения натуральных чисел называют их произведением. Произведение двух натуральных чисел $a$ и $b$ содержит стольких единиц, сколько их содержится в числе $a$, взятых столько раз, сколько единиц содержится в числе $b$.
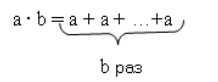
Рисунок 1.
Если произведение обозначить $c$, то говорят, что оно получено в результате умножения чисел $a$ и $b$. Записывается умножение двух чисел следующим образом:
$acdot b=c$ или $atimes b=c$.
Числа $n$ и $m$ называют множителями или сомножителями.
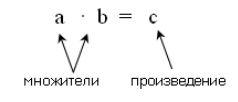
Рисунок 2.
Например, найдем произведение чисел $13cdot 5$.
По определению операции умножения:
Свойства умножения натуральных чисел
Умножение натуральных чисел характеризуется следующими свойствами:
Коммутативность умножения:
[acdot b=bcdot a.]
Ассоциативность умножения:
[left(acdot bright)cdot c=acdot left(bcdot cright)]
Пример 1
Например, найдем произведение чисел $9cdot 15cdot 6$.
Применим к данному произведению свойство ассоциативности умножения:
[9cdot 15cdot 6=9cdot left(15cdot 6right)=9cdot 90=810]
Из свойства ассоциативности умножения натуральных чисел выводится понятие натуральной степени натурального числа:
Натуральное число m в степени n равно натуральному числу $k$, которое получается в результате умножения числа $m$ самого на себя $n$ раз:
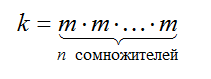
Рисунок 3.
Для обозначения $n$-й степени числа m используют запись $m^n$, в которой число $m$ называется основанием степени, а число $n$ – показателем степени.
Пример 2
Например, найдем значение выражения $3^4$.
По определению натуральной степени натурального числа данное выражение можно записать так:
[3^4=3cdot 3cdot 3cdot 3=81.]
Получили $3^4=81$.
Закон дистрибутивности умножения относительно сложения:
[left(a+bright)cdot c=acdot c+bcdot c.]
Закон дистрибутивности умножения относительно вычитания:
[left(a-bright)cdot c=acdot c-bcdot c.]
В результате нахождения суммы и произведения двух натуральных чисел всегда получится натуральное число.
Свойство умножения на единицу:
[acdot 1=1cdot a=a.]
Свойство умножения на нуль:
[acdot 0=0cdot a=0.]
Свойство умножения нулей:
[0cdot 0=0.]
Свойство умножения единиц:
[1cdot 1=1.]
Операцию умножения натуральных чисел удобно выполнять «в столбик»:
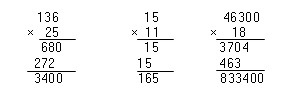
Рисунок 4.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Деление натуральных чисел
Операция деления натуральных чисел является обратной операцией к умножению.
Результат деления натуральных чисел называют их частным.
Если $bcdot c=a$, то
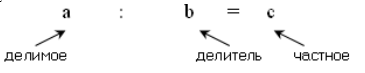
Рисунок 5.
Свойства деления натуральных чисел
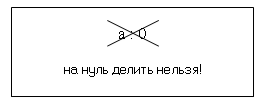
Рисунок 6.
Свойство деления произведения на число:
[left(acdot bright):c=left(a:cright)cdot b,] [left(acdot bright):c=left(b:cright)cdot a,] [left(acdot bright):c=a:left(bcdot cright).]
Свойство деления на единицу:
[a:1=a.]
Свойство деления двух равных натуральных чисел:
[a:a=1, ane 0.]
Свойство деления нуля на натуральное число:
[0:a=0, ane 0.]
Выполнять деление двух натуральных чисел удобно методом «угла»:
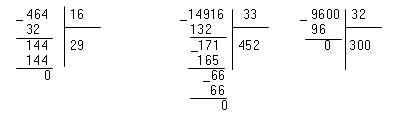
Рисунок 7.
В результате нахождения разницы и при делении натуральных чисел натуральное число можно получить не для любой пары натуральных чисел.
Пример 3
Например, числа $15$ и $5$ — натуральные. Результат вычитания $15-5=10$ также будет натуральным числом, а если найти разницу натуральных чисел $5-15=-10$, то получим число, которое уже не является натуральным.
Таблица умножения натуральных чисел
По определению произведения двух натуральных чисел можно получить результаты умножения однозначных натуральных чисел. Например, произведение $5cdot 4$ равно сумме $4$ одинаковых слагаемых, которые равны $5$. В таком случае получаем $5cdot 4=5+5+5+5=20$. Аналогично можно получить результат произведений всех однозначных натуральных чисел и записать их в таблицу.
Результаты произведений удобно представлять в виде так называемой таблицы умножения.
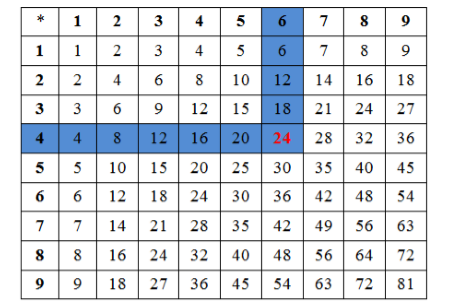
Рисунок 8.
Правила пользования таблицей умножения
Пример 4
Например, нужно найти произведение чисел $4$ и $6$. Для этого отметим столбец (выделен синим цветом), в верхней ячейке которого записано число $6$, и строку (выделена синим цветом), в левой ячейке которой записано число $4$. Результат умножения находится на пересечении отмеченных столбца и строки — число $24$, отмеченное красным цветом.
Аналогично можно найти произведение остальных чисел, но принято знать таблицу умножения наизусть.
Источник
Умножение, сложение, вычитание и деление – основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.
Сложение целых чисел. Основные свойства
Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ. Приведем ниже основные свойства сложения.
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
a+b=b+a
Согласно этому свойству, справедливо равенство:
35+251=251+35
Свойство коммутативности работает вне зависимости от знака.
-528+3700=3700+-528
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a+b+c=a+b+c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
64+81+(-49)=64+81+(-49)=64+81+(-49);
(128+(-75))+96=128+((-75)+96).
Свойства сложения, связанные с числом 0
1. Число нуль – нейтральный по сложению элемент.
Прибавление нуля к любому целому числу не меняет этого числа.
a+0=a
2. Сумма любого целого числа и противоположного ему числа равна нулю.
a+(-a)=0
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
a·b=b·a
Приведем пример. Очевидно, что произведение целых чисел 2·3 эквивалентно произведению 3·2.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a·(b·c)=(a·b)·c
a, b, c – произвольные целые числа.
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
-12·3·8=-12·3·8;
119·((-251)·36)=(119·(-251))·36.
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
a·0=0
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
a·b=0 если a=0 или b=0.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a·1=a
Распределительное свойство умножения относительно суммы.
Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a·b и a·c.
a·(b+c)=a·b+a·c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Вычитание – действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b+c равна a. Можно сказать, что разность чисел a и b – это сумма чисел a и -b. Свойства вычитания являются следствием свойств сложения и умножения.
Основные свойства вычитания
- Вычитание чисел не обладает переместительным свойством за исключением случая, когда a=b. a-b≠b-a.
- Разность целых чисел, равных друг другу: a-a=0.
- Вычитание суммы двух чисел из другого числа: a-(b+c)=a-b-c.
- Вычитание целого числа из суммы: a+b-c=a-c+b=a+(b-c).
- Распределительное свойство умножения относительно вычитания: a·(b-c)=a·b-a·c.
Деление целых чисел. Основные свойства
Деление – операция, обратная умножению. Число c называется частным от деления чисел a и b, когда произведение b·c равно a. Запишем основные свойства деления целых чисел.
Основные свойства деления
- Деление на нуль невозможно.
- Деление нуля на число: 0a=0.
- Деление равных чисел: aa=1.
- Деление на единицу: a1=a.
- Для деления переместительное свойства не выполняется: ab≠ba.
- Деление суммы и разности на число: a±bc=ac±bc.
- Деление произведения на число: a·bc=ac·b, если a делится на c; a·bc=a·bс, если b делится на c; a·bc=a·bс=ac·b, если a и b делятся на c.
- Деление числа на произведение: ab·c=ab·1c=ac·1b.
Источник
