Какие цифры содержатся в пятеричной системе счисления

Содержание:
Что такое пятеричная система счисления
Как перевести целое десятичное число в пятеричную систему счисления
Как перевести десятичную дробь в пятеричную систему счисления
Как перевести число из пятеричной системы счисления в десятичную
Как перевести дробное пятеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в пятеричной системе счисления
Что такое пятеричная система счисления
Пятеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.
Для записи числа в пятеричной системе счисления используется пять цифр 0, 1, 2, 3 и 4.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, 13045 или 20335
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в пятеричную систему счисления
Для того, чтобы перевести целое десятичное число в пятеричную систему счисления нужно десятичное число делить на 5 до тех пор, пока неполное частное не будет равно нулю.
В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 7010 в пятеричную систему счисления:
70 : 5 = 14 остаток: 0
14 : 5 = 2 остаток: 4
2 : 5 = 0 остаток: 2
7010 = 2405
Как перевести десятичную дробь в пятеричную систему счисления
Для того чтобы перевести десятичную дробь в пятеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в пятеричную систему счисления,
а затем дробную часть, последовательно умножать на 5, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 4.310 в пятеричную систему счисления:
Переведем целую часть
4 : 5 = 0 остаток: 4
410 = 45
Переведем дробную часть
0.3 · 5 = 1.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.310 = 0.12222222225
4.310 = 4.12222222225
Пятеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной пятеричной.
В данном примере получается бесконечная периодическая пятеричная дробь, поэтому умножение на 5 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 4.3 не может быть точно представлена в пятеричной системе счисления.
К примеру, дробь 12.3610 может быть представлена в пятеричной системе счисления в виде конечной 12.3610 = 22.145.
Как перевести число из пятеричной системы счисления в десятичную
Для того, чтобы перевести число из пятеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 5, так как система счисления 5-ичная. Необходимо последовательно умножить каждое число на 5 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число 40235 в десятичную систему счисления:
| Позиция в числе | 3 | 2 | 1 | |
| Число | 4 | 2 | 3 |
40235 = 4 ⋅ 53 + 0 ⋅ 52 + 2 ⋅ 51 + 3 ⋅ 50 = 51310
Как перевести дробное пятеричное число в десятичное
Для того, чтобы перевести дробное пятеричное число в десятичное, необходимо записать дробное пятеричное число, убрав точку и затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 5, так как система счисления 5-ичная. Необходимо последовательно умножить каждое число на
5 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное пятеричное число 21.135 в десятичное:
| Позиция в числе | 1 | -1 | -2 | |
| Число | 2 | 1 | 1 | 3 |
21.135 = 2 ⋅ 51 + 1 ⋅ 50 + 1 ⋅ 5-1 + 3 ⋅ 5-2 = 11.3210
Таблица значений десятичных чисел от 0 до 100 в пятеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в пятеричной системе счисления |
| 010 | 05 |
| 110 | 15 |
| 210 | 25 |
| 310 | 35 |
| 410 | 45 |
| 510 | 105 |
| 610 | 115 |
| 710 | 125 |
| 810 | 135 |
| 910 | 145 |
| 1010 | 205 |
| 1110 | 215 |
| 1210 | 225 |
| 1310 | 235 |
| 1410 | 245 |
| 1510 | 305 |
| 1610 | 315 |
| 1710 | 325 |
| 1810 | 335 |
| 1910 | 345 |
| 2010 | 405 |
| 2110 | 415 |
| 2210 | 425 |
| 2310 | 435 |
| 2410 | 445 |
| 2510 | 1005 |
| 2610 | 1015 |
| 2710 | 1025 |
| 2810 | 1035 |
| 2910 | 1045 |
| 3010 | 1105 |
| 3110 | 1115 |
| 3210 | 1125 |
| 3310 | 1135 |
| 3410 | 1145 |
| 3510 | 1205 |
| 3610 | 1215 |
| 3710 | 1225 |
| 3810 | 1235 |
| 3910 | 1245 |
| 4010 | 1305 |
| 4110 | 1315 |
| 4210 | 1325 |
| 4310 | 1335 |
| 4410 | 1345 |
| 4510 | 1405 |
| 4610 | 1415 |
| 4710 | 1425 |
| 4810 | 1435 |
| 4910 | 1445 |
| 5010 | 2005 |
| Значение числа в десятичной системе счисления | Значение числа в пятеричной системе счисления |
| 5110 | 2015 |
| 5210 | 2025 |
| 5310 | 2035 |
| 5410 | 2045 |
| 5510 | 2105 |
| 5610 | 2115 |
| 5710 | 2125 |
| 5810 | 2135 |
| 5910 | 2145 |
| 6010 | 2205 |
| 6110 | 2215 |
| 6210 | 2225 |
| 6310 | 2235 |
| 6410 | 2245 |
| 6510 | 2305 |
| 6610 | 2315 |
| 6710 | 2325 |
| 6810 | 2335 |
| 6910 | 2345 |
| 7010 | 2405 |
| 7110 | 2415 |
| 7210 | 2425 |
| 7310 | 2435 |
| 7410 | 2445 |
| 7510 | 3005 |
| 7610 | 3015 |
| 7710 | 3025 |
| 7810 | 3035 |
| 7910 | 3045 |
| 8010 | 3105 |
| 8110 | 3115 |
| 8210 | 3125 |
| 8310 | 3135 |
| 8410 | 3145 |
| 8510 | 3205 |
| 8610 | 3215 |
| 8710 | 3225 |
| 8810 | 3235 |
| 8910 | 3245 |
| 9010 | 3305 |
| 9110 | 3315 |
| 9210 | 3325 |
| 9310 | 3335 |
| 9410 | 3345 |
| 9510 | 3405 |
| 9610 | 3415 |
| 9710 | 3425 |
| 9810 | 3435 |
| 9910 | 3445 |
| 10010 | 4005 |
Источник
Рассмотрим два основных арифметических действия: сложение и умножение в различных
системах счисления.
Пятеричная система счисления
Сложение
Составим таблицу сложения для пятеричных цифр (будем использовать ее при
сложении чисел в «столбик»).
| Найдем 2345 + 3125. Складывать будем поразрядно в «столбик», |
Вычитание
Используя таблицу сложения можно также и вычитать числа в пятеричной системе счисления:
| Найдем 2035 345. Вычитать будем поразрядно в «столбик», |
Сложение и вычитание можно выполнять и не используя таблицу сложения.
Необходимо помнить:
- при сложении чисел в пятеричной системе счисления,
единицу в старший разряд мы переносим, когда в сумме получилось не 10, а 5! - при вычитании в старшем разряде мы занимаем не 10, а 5 единиц.
Если выполнение операций сложения и вычитания поручить формальному исполнителю,
например компьютеру, тогда необходимо хранить в его памяти таблицу сложения, т.е.
5*5=25 ячеек памяти будет занято под таблицу.
Умножение
Составим таблицу умножения для пятеричной системы
счисления (цифру 0 не включаем, т.к. умножение на 0 всегда равно 0).
| Найдем 135 * 245. Умножать будем в «столбик», |
| Вывод: | Для выполнения арифметических операций в пятеричной системе счисления необходимо запомнить 25 правил сложения и 16 правил для умножения. . |
Столько правил необходимо было бы «запомнить» компьютеру, если бы он работал в
пятеричной системе счисления.
Сравните с «нашей» десятичной системой счисления:
10*10 = 100 правил сложения и 9*9 = 81 правило умножения!
Двоичная система счисления
Составим таблицы сложения и умножения для двоичной системы счисления.
| 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 | 0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1 |
| Вывод: | Для выполнения арифметических операций в двоичной системе счисления необходимо запомнить всего 4 правила сложения и 1 правило умножения. . |
Вот еще один аргумент за то, что вся информация в памяти компьютера храниться в
двоичном коде (в виде 0 и 1).
Рассмотрим примеры сложения и вычитания в двоичной системе счисления.
Необходимо помнить:
- при сложении чисел в двочной системе счисления,
единицу в старший разряд мы переносим, когда в сумме получилось не 10, а 2! - при вычитании в старшем разряде мы занимаем не 10, а 2 единицы.
Троичная система счисления
Заполните самостоятельно таблицы сложения и умножения для троичной системы
счисления.
Источник

=============================================================================================================
Немного истории
Счёты – это первое простейшее устройство для вычислений. Почти с начала 19 века счёты не меняются и становятся такими, какими мы их видим сегодня, а в дальнейшем совершенствуются в основном разве что внешне, с точки зрения удобства пользования и вплоть до 70-х годов ХХ-века являлись наиболее массовым вспомогательным вычислительным устройством. Начиная с 70-х годов с ними начинают конкурировать электронные калькуляторы, счеты и в наше время ещё можно встретить, хотя уже очень редко.
Русские счеты, XVI в. с десятичной системой счисления создаются примерно в это время.Ранее считалось, что русские счеты ведут свое происхождение от китайского суаньпаня, и только лишь в начале 50-х годов прошлого столетия ленинградский ученый И.Г. Спасский убедительно показал что это русское, так как у этого прибора, во-первых, горизонтальное расположение спиц с косточками и, во-вторых, для представления чисел использована десятичная , а не пятеричная система счисления. (Помните как в сказке Конёк-горбунок царь спрашивает Ивана-дурочка: ” Что в замен хотишь добра” и тот отвечает:” Два-пять шапок серебра”. ) Десятичный строй счетов — довольно веское основание для того, чтобы признать временем возникновения этого прибора XVI век, когда десятичный принцип счисления был впервые применен в денежном деле России.
Широкое использование в торговле невиданного на Западе счетного инструмента отмечали в XVII—XVIII столетиях многие иностранцы. Английский капитан Перри, находившийся в России с 1698 по 1712 год и издавший по возвращению на родину книгу в которой он писал:“Для счета они (русские) пользуются изобретенным ими особым прибором с нанизанными на проволочные прутья шариками от четок или бусами, который они устраивают в ящике или небольшой раме, … Передвигая туда и сюда шарики, они справляются с делением и умножением разных сумм…”
Счёты в то время уже представляли лишь одно счетное поле, на спицах которого размещались либо 10, либо 4 косточки (спица с 4 четками — это дань “полушке”, русской денежной единице в 1/4 копейки).
Пятеричная система счисления
Число в пятеричной системе изображается пятью цифрами: 0, 1, 2, 3, 4. В этой системе цифра 4 – наибольшая (как 9 – в десятичной), единица высшего разряда не в 10, а в 5 раз больше единицы низшего.
Единица второго разряда – это пять.
Единица третьего разряда – “25”, так как 5•5=25
Единица четвертого разряда – “125”, так как 25•5=125
Единица пятого разряда – “625”, так как 125•5=625 и т.д.
При изображении числа в пятеричной системе счисления, на первом месте справа стоят простые единицы (не свыше 4), на втором – не десятки, а пятерки, на третьем – не сотни, а “25” и т.д.
Пример:
Число 139 изобразить в пятеричной системе.
Делим 139 на 5, чтобы узнать, сколько в нем единиц первого разряда:
139:5=27, остаток 4. Значит, число простых единиц будет 4.
Далее, 27 пятёрок не могут стоять все во втором разряде, т.к. высшая цифра в пятеричной системе – 4, и больше 4 единиц ни в одном разряде быть не должно, делим 27 на 5 (27:5=5, остаток 2), значит это показывает, что во втором разряде (“5”) будет цифра 2.
В третьем разряде (“25”) – цифра 4.
Итак: 139 = 5•25 + 2•5 + 4 или в пятеричной системе 524.
Десятичная система счисления
Современная десятичная система счисления это десять цифр – от 0 до 9.
Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Десять пальцев рук – вот аппарат для счета, которым человек пользуется с доисторических времен.
Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 – углов нет, 2 – два угла и т.д.
![]()
Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Наряду с появлением письменности, возникновение и развитие десятичной системы счисления явилось одним из важнейших достижений человечесва.
Источник
Мы подошли к 14 заданию из ЕГЭ по информатике 2021. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 – 25 записали в системе счисления с основанием 5. Сколько цифр “4” содержится в этой записи?
Решение:
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.

Примеры:
54 (в десятичной системе) – это 100005 (в пятеричной системе)
72 (в десятичной системе) – это 1007 (в семеричной системе)
29 (в десятичной системе) – это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 – 52
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.

Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
Теперь от получившегося числа нужно отнять 52 (1005).
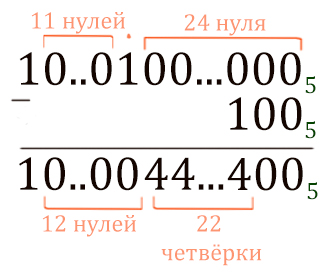
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
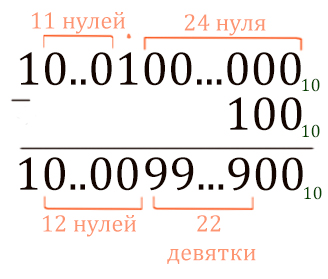
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 168 × 420 – 45 – 64 записали в системе счисления с основанием 4. Сколько цифр “3” содержится в этой записи?
Решение:
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 – 45 – 64 =
= (42)8 × 420 – 45 – 43 =
= 416 × 420 – 45 – 43 =
= 436 – 45 – 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 436 – 45.
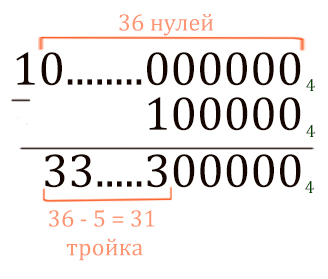
Теперь от этого числа нужно отнять 43 (10004)

Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.

Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
1) Переведём число 17 в троичную систему.
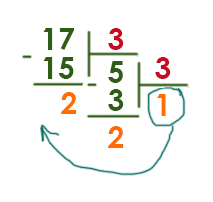
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2021.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени – это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2×2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 2 :
x (1 + x) = 2 × 22 = 8 ; нет последовательных чисел, которые при умножении дают 8, ищем дальше
При y = 3 :
x (1 + x) = 2 × 32 = 18 ; нет последовательных чисел, которые при умножении дают 18, ищем дальше
При y = 4 :
x (1 + x) = 2 × 42 = 32 ; нет последовательных чисел, которые при умножении дают 32, ищем дальше
При y = 5 :
x (1 + x) = 2 × 52 = 50 ; нет последовательных чисел, которые при умножении дают 50, ищем дальше
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2021 разберём ещё некоторые задачи.
Задача (Основание системы)
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
Чтобы перевести число из нашей родной системы счисления в любую другую систему с основанием N, нужно начать делить это число уголком на N.
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
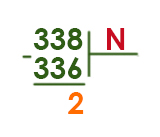
Число 336 должно делится на N.
Сказано, что число в системе счисления с основанием N должно быть трёхзначное. Оценим примерные границы числа N, чтобы число было трёхзначным.
Оценим примерную верхнюю границу для N. Если, что N = 20, то 338 : 20 = 16 (ост. 18). Видим, что при одном делении мы получаем число 16, т.е. число меньше, чем 20. Значит, если бы мы переводили число 338 в двадцатеричную систему, получили бы двухзначное число.
Значит, N
Найдём число, которое меньше 20, и является делителем числа 336. Начинаем перебирать с наибольших чисел.
Подошло число 16 (16 * 21 = 336!)
Проверим, что это число нам подходит на 100 %.

Видим, что мы выполнили все условия задачи и нашли число N максимально возможное.
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2021
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
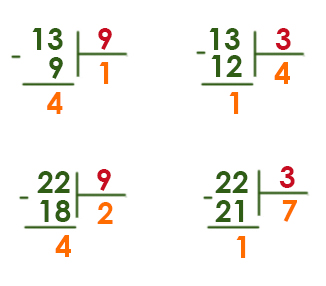
Ответ: 1
Задача (Закрепление материала)
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) –
23 : 5 = 4 (ост. 3) –
23 : 6 = 3 (ост. 5) –
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) –
23 : 9 = 2 (ост. 5) –
23 : 10 = 2 (ост. 3) –
23 : 11 = 2 (ост. 1) –
23 : 12 = 1 (ост. 11) –
23 : 13 = 1 (ост. 10) –
23 : 14 = 1 (ост. 9) –
23 : 15 = 1 (ост. 8) –
23 : 16 = 1 (ост. 7) –
23 : 17 = 1 (ост. 6) –
23 : 18 = 1 (ост. 5) –
23 : 19 = 1 (ост. 4) –
23 : 20 = 1 (ост. 3) –
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) –
23 : 23 = 1 (ост. 0) –
Подходят числа 3, 7, 21.
Ответ: 3, 7, 21
Задача (Добъём 14 задание из ЕГЭ по информатике 2021)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не “поместилась” в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2021. Успехов на экзамене!
Источник
