Какие общие свойства имеют ромб и квадрат

Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
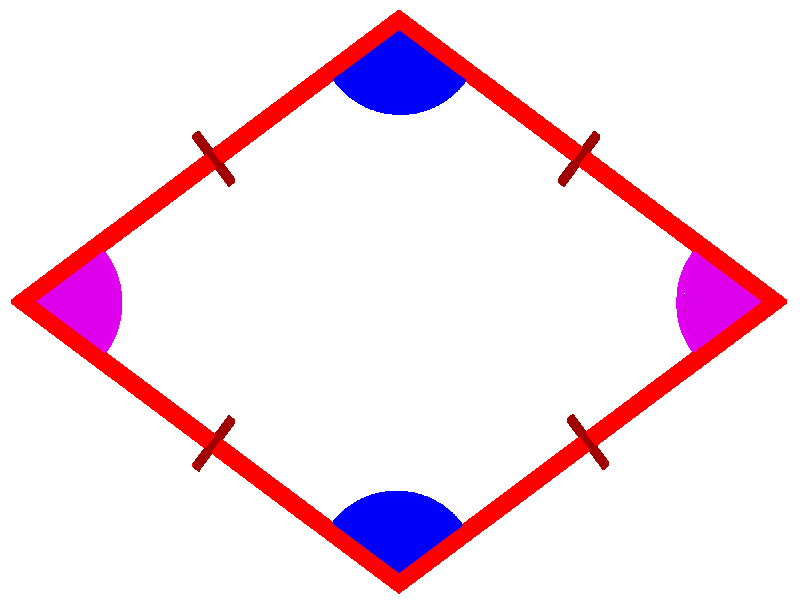
Источник:
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
Источник:
С квадратом все намного проще, его определение звучит так: квадрат – это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:
Понравился пост? Поддержи Фишки, нажми:
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Ромб и квадрат
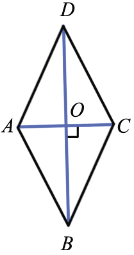
Частным видом параллелограмма является ромб.
Ромбом называется параллелограмм, у которого все стороны равны
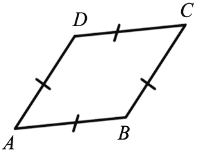
ABCD – ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
Доказательство
Дано: ABCD – ромб
Доказать: ACBD, ADO = CDO
Доказательство:
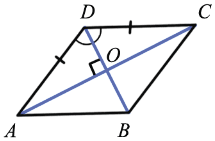
AD = DC (по определению ромба), значит, ADC – равнобедренный.
AO = OC (по свойству диагоналей параллелограмма), DO – медиана ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой, ACBD, ADO = CDO, что и требовалось доказать.
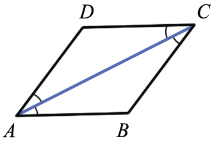
Теорема
Доказательство
Дано: ABCD – параллелограмм, ACBD
Доказать: ABCD – ромб
Доказательство:
Рассмотрим AOВ и COВ:
Т.к. ACBD, тоAOВ = COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ – общий катет, AOВ = COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны, ВС = ВА.
В параллелограмме противоположные стороны равны, AD = BC, AB = DC
Итак: ABCD – параллелограмм (по условию) AD = BC =AB = DC (по доказанному). ABCD – ромб, что и требовалось доказать.
Теорема
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб
Доказательство
Дано: ABCD – параллелограмм, АС – диагональ и биссектриса DAB иDCB
Доказать: ABCD – ромб
Доказательство:
DAB =DCB (по свойству параллелограмма), а АС -биссектриса DAB иDCB (т.е. АС делит эти углы на два равных угла), DAC = BAC =DCA = BCA
Рассмотрим ADC: DAC =DCA, ADC – равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны, AD = BC, AB = DC
Итак: ABCD – параллелограмм (по условию) AD = BC =AB = DC (по доказанному). ABCD – ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
Основные свойства квадрата:
1. Все углы квадрата прямые.
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Прямоугольник
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 451,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 633,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 693,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 818,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1032,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1080,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1132,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1152,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1290,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1305,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
В статье описываются геометрические фигуры: определение, основные свойства и формулы.
Плоские геометрические фигуры:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность
Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.
Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Источник
Тип урока: урок «открытия» новых знаний.
Цель урока:
Деятельностная цель: формирование у обучающихся умение реализовать новые способы действий (формулировка определений ромба и квадрата).
Образовательная цель: расширение понятийной базы за счет включения в нее новых элементов (примеры с использованием свойств ромба и квадрата).
Планируемые результаты
Личностные УУД: Формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний.
Метапредметные УУД:
Регулятивные: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и оценивать свои достижения.
Познавательные: формировать навыки решения задач с использованием свойств ромба и квадрата; формировать умения применять полученные знания при решении более сложных задач.
Коммуникативные: воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
Задачи:
Рассмотреть понятие ромба и квадрата как частных видов параллелограмма.
Рассмотреть свойства и признак ромба, квадрата.
Применять свойства в процессе решения задач.
Воспитывать дисциплинированность, ответственное отношение к учебному труду.
Вид урока: урок – исследование
Формы организации деятельности: фронтальная, индивидуальная.
Методы обучения: беседа, проблемная ситуация, устный и письменный контроль.
Средства: учебник, компьютер, фигурки трёх цветов, раздаточный материал с устными заданиями и теоретической самостоятельной работой.
Литература: учебник «Геометрия, 7- 9 классы», автор Л.А.Атанасян и другие.
План урока:
1. Организационный момент (2 мин.).
2. Актуализация знаний (4 мин.).
3. Мотивация. Целеполагание. (3 мин)
4. Открытие новых знаний (15 мин.).
5. Физическая минутка (2 мин.).
6. Первичное закрепление пройденного материала (10мин.).
7. Домашнее задание (1мин.).
8. Итог урока. Рефлексия (3 мин.).
Ход урока
Тот ничего не изучает,
Кто ничего не замечает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Приветствуют учителя.
Организация внимания обучающихся
2
Математический диктант
Вариант 1
1. Является ли прямоугольником параллелограмм, один из углов которого прямой?
2. Правильно ли, что каждый прямоугольник является параллелограммом?
3. Диагонали прямоугольника АЕКМ пересекаются в точке О. Отрезок АО равен
3 дм. Найдите длину диагонали ЕМ.
4. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник является прямоугольником?
Вариант 2
1. Обязательно ли четырехугольник с прямым углом является прямоугольником?
2. Правильно ли, что каждый параллелограмм является прямоугольником?
3. Диагонали параллелограмма имеют длину 3дм и 5 дм. Или этот параллелограмм является прямоугольником?
4. Сумма длин диагоналей прямоугольника равна 13м. Найдите длину каждой диагонали.
Перед выполнением математического диктанта следует напомнить ученикам правила выполнения его задач, а именно: условие задач не записывается (ученики должны записать только номер вопроса), ответ должен быть кратким, но содержательным
(т. е. в ответе должна быть аргументация — ссылка на соответствующее геометрическое утверждение).
Выполняют.
Активизация знаний обучающихся, необходимых для изучения нового материала.
3
Каким образом из произвольного параллелограмма образовалась новая фигура — прямоугольник ?(если все углы параллелограмма «сделать» равными, то «получится» прямоугольник).
Какие еще элементы параллелограмма можно сделать равными?» Конечно, большинство учеников дает правильный ответ (стороны). После чего формулируется следующий вопрос: «существует ли параллелограмм, у которого все стороны и углы равны?» Получив утвердительный ответ, учитель выделяет таким образом две новые (то есть те, которые ранее не изучались на уроках геометрии) геометрические объекты. Изучение определения, свойств и, возможно, признаков этих фигур, овладение способами их применения является основной дидактической целью урока.
Отвечают на вопросы.
Предполагают.
Формирование мотивации обучающихся. Подталкивание обучающихся к самостоятельному озвучиванию темы и целей урока.
4
Задание №1 Сейчас я предлагаю вам поработать в роли исследователей. Вы должны построить в тетрадях параллелограмм, у которого, диагонали взаимно перпендикулярны. Для этого еще раз вспомним, что диагонали параллелограмма …? (точкой пересечения делятся пополам)
Сравните длины сторон этого параллелограмма (ученики делают вывод, что стороны параллелограмма равны)
Итак, перед нами параллелограмм, у которого все стороны равны. Это новая фигура? Да. Значит ей необходимо дать новое название.
И эту фигуру назвали РОМБОМ.
Кто же может сформулировать определение ромба? (Ученики стараются дать определение) и записывают в тетрадь.
Ромб, как и изученные нами фигуры, имеет свои свойства.
Давайте, постараемся их сформулировать (сторон, углов, диагоналей) Как вы думаете, свойства какой фигуры будут справедливы и для ромба? (параллелограмма)
А) стороны попарно параллельны
Б) стороны равны
В) противоположные углы равны
У ромба есть свое отличительное свойство . Мы его сейчас запишем и докажем
Диагонали пересекаются и точкой пересечения делятся пополам (Ученики самостоятельно доказывают особое свойство ромба без записи в тетрадях)
Особое свойство ромба Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Дано АВСD – ромб,
АС и ВD – диагонали
Доказать:
1. АС ┴ BD
2. <ВАС = <DAC.

Доказательство.
1 Так, как АВСD ромб, то по определению АВ АD.
2. ∆ ВАD – ______________________________.
3 Так как ВО__ ОD, значит АО ________________равнобедренного треугольника , а следовательно ______________________________________________________________.
4. Поэтому АС __ BD и <ВАС ___< DAC.
Что и требовалось доказать.
Задание №2 Посмотрите на наш рисунок и скажите какую, хорошо вам известную, фигуру он вам напоминает, если ромб повернуть на 90 градусов – КВАДРАТ .Почему вы так решили? Стороны равны и углы прямые. Свойства каких двух фигур можно объединить в квадрате? Кто поможет сформулировать определение квадрата?
Квадратом – называется прямоугольник…
Перечисляются свойства квадрата
АВ||СD, BC||AD – стороны попарно параллельны
AB=BC=CD=AD – все стороны равны
угол A = угол B= угол C= угол D=90° – все углы равны
AO=BO=CO=DO – отрезки диагоналей равны
AC перпендикулярен BD – диагонали перпендикулярны
Каждая диагональ является биссектрисой угла
Строят.
Дают определение и записывают.
Формулируют свойства, записывают.
Доказывают.
Предполагают.
Дают определение квадрата.
Перечисляют свойства квадрата и записывают.
«Открытие» новых знаний.
5
( «Истинно-ложно»)
Я скажу несколько математических предложений. Если предложение верное, то вы сидите, если оно ложное, то вы встаёте, и кто-то из вас объясняет, почему ложное.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. (+)
В параллелограмме противоположные стороны и противоположные углы равны. (+)
В параллелограмме диагонали равны. (-)
В параллелограмме диагонали точкой пересечения делятся пополам. (+)
Диагонали прямоугольника точкой пересечения делятся пополам. (+)
Сумма углов выпуклого четырёхугольника равна 180◦. (-)
В прямоугольнике противоположные стороны равны. (+)
Ромб обладает всеми свойствами прямоугольника. (-)
Квадрат не обладает всеми свойствами ромба. (-)
Квадрат обладает всеми свойствами параллелограмма, прямоугольника, ромба (+)
Выполняют.
Эмоциональная и физическая разгрузка.
6
Выполнение устных упражнений
1. Назовите виды параллелограммов, в которых: а) все углы равны; б) все стороны равны; в) диагонали равны; г) диагонали перпендикулярны.
2.Диагонали квадрата ABCD пересекаются в точке О. Назовите все равные треугольники, которые образуются при пересечении диагоналей. Определите ее вид.
Выполнение письменных упражнений
1. Найдите углы ромба, если:
а) один из них на 120° больше другого;
б) одна из его диагоналей равна стороне.
2. Найдите углы ромба, если:
а) углы, образованные его стороной с диагоналями, относятся как 1 : 4;
б) высота ромба вдвое меньше стороны.
3. Периметр квадрата равен 40 м. Найдите расстояние от точки пересечения диагоналей квадрата до его стороны.
4*. В равнобедренный прямоугольный треугольник вписан квадрат, две вершины которого лежат на гипотенузе треугольника, две другие — на катетах. Найдите периметр квадрата, если гипотенуза равна 18 см.
Теоретическая самостоятельная работа. (Самоанализ и самооценка)
– Заполните таблицу, отметив знаки + (да) и – (нет).
Листки сдаются учителю.
Критерий выставления оценки:
Оценка «5» – все ответы верные.
Оценка «4» – допущено 1-5 ошибок.
Оценка «3» – допущено 5-10 ошибок.
Оценка «2» – допущено более 10 ошибок.
Решают.
Выполняют СР и проверяют, выставляют оценки.
Воспроизведение изученного материала на уровне логических рассуждений.
7
Выучить определения и свойства. Решить задачи:
1. Найдите углы ромба, если:
а) сумма двух из них равна 220°;
б) диагональ образует с одной из сторон угол 25°.
2. Расстояние между противоположными сторонами квадрата равна 5 см. Найдите периметр квадрата.
Или №406, 409
Записывают домашнее задание.
Дальнейшее самостоятельное применение полученных знаний.
8
1. Какие общие свойства имеют ромб и квадрат?
2. Какие свойства квадрата не характерны для прямоугольника?
3. Является квадратом:
а) прямоугольник ABCD, диагональ AC которого является биссектрисой угла BAD;
б) ромб, диагонали которого равны;
в) параллелограмм, диагонали которого взаимно перпендикулярны;
г) четырехугольник, все стороны которого равны?
Хорошо усвоил материал, то поднимают красные фигурки,
есть непонятные вопросы – синие,
плохо усвоил – желтые.
Отвечают, предполагают.
Поднимают.
Подведение итогов, установление соответствия между полученным и запланированным результатом.
Рефлексия деятельности.
Урок подготовила и провела:
учитель математики I категории
МБОУ Ваховская ОСШ
З.Н.Ахунова
Источник
