Какие свойства дробей вы знаете

Общие сведения
Дробь — это число, образуемое из равных долей единицы. Чтобы разобраться в сути выражения, следует понять, что означают слова «целое» и «часть». Пусть есть плитка шоколадки. Она разделена на десять частей. Если взять один кусочек, можно сказать, что в руках находится одна часть из десяти. Отломать второй — получится два куска опять же из десяти.
Эти кусочки и являются долями. То есть тем, из чего состоит целая часть. При этом их размеры должны быть одинаковыми. В рассматриваемой шоколадке их десять. Если её поделить пополам, то это действие будет сродни удалению пяти долей. На математическом языке это действие будет записано как 5 / 10. Целую же шоколадку можно представить так: 10 / 10.
Наклонная черта обозначает деление. В верхней части записывают число, определяющее, сколько долей было забрано от целого, значение которого указывается в нижней строке. В математике принято для краткости число, стоящее над чертой, называть числителем (делимым), а под ней знаменателем (делителем).
В зависимости от значений отношения, существующие дробные выражения разделяют на три типа:
- правильные — делимое по количеству меньше делителя;
- неправильные — значение числителя больше, чем знаменателя;
- смешанные — состоят из целой части и неправильного выражения;
- многоэтажные — в числителе или знаменателе стоят дробные числа, например, (7/8) / 2.
Существуют и так называемые десятичные дроби. Их исторически выделили из-за простоты выражения. При этом в записи используется не черта, а запятая. Она отделяет единицы от десятичных значений. Например, 1,2; 0,2; 3,56. Это просто иные записи обыкновенных дробных выражений. Так: 1,2 = 12 / 10; 0,2 = 2 /10; 3,56 = 356 / 100.
Пожалуй, понятие смешанной дроби требует дополнительного объяснения. Записывают её так: x (y / z), где: x — целое число; y / z — дробное отношение. По сути, между двумя частями стоит знак плюс, который не указывают. Поэтому выражение x (y / z) можно переписать как x (y / z) = x + (y / z). Например, 3 (4/5) = 3 + (4 / 5).
Так как дроби это числа, то с ними можно выполнять любые арифметические операции. Но их можно не только складывать, вычитать, умножать, делить, но и возводить в степень, дифференцировать, брать логарифм. Для выполнения этих действий нужно знать правила и свойства дробей, которым и обучают на уроках математики в школе.
Главное правило
Основное свойство дроби заключается в том, что если числитель и знаменатель умножить на одно и то же число, то результат действия от этого не изменится. Это правило справедливо и для операции деления. Доказать это утверждение довольно просто.
Пусть есть два равных выражения a / b и m / n. Они будут равными, если у них одинаковые числители и знаменатели. Значит: a * n = b * m. Например, 3 / 5 = 6 / 10, так как 3 * 10 = 5 * 6. Из этого следует, что одинаковыми будут по величине и выражения a / b = (m * c) / n * c), ведь равенство a * (n * c) = b * (m * c) также справедливо. Утверждать о верности последнего выражения можно на основании сочетательного и переместительного свойства умножения.

Эти правила гласят следующее:
- для любых натуральных чисел верно равенство a * b = b * a;
- результат перемножения трёх и более аргументов не поменяется, если группу членов заменить произведением a · b · c = (a · b) · c = a · (b · c).
Таким образом, можно записать: a / b = a * c / b * c. Это равенство и соответствует основному свойству дроби. В 5 классе после доказательства правильности утверждения, ученикам предлагается подумать над следствием, вытекающим из правила. На самом деле оно простое и порядка 90 процентов учеников называют его. Звучит оно так: если в дробном выражении делимое и делитель разделить на одно и то же число, значение выражения не изменится.
Эти правила очень важны. Благодаря им исходное равенство можно при необходимости привести к простому виду. Использование следствия иногда называют сокращением дроби. Например, пусть есть простое для понимания отношение: 60 / 30. Если выполнить деление, то в ответе получится цифра два. Но изначально числитель и знаменатель можно сократить на десять, то есть разделить на это число: 60 / 30 = 6 / 3 = 2. Результат не поменялся. Более того, можно упростить и 6 / 3, выполнив деление на три: 6 / 3 = 2 / 1 = 2. Ответ снова совпадает.

Для общего же случая нужно отметить, что сокращение возможно лишь тогда, когда делимое и делитель не являются взаимно простыми числами. Если это не так, то дробь считается несократимой. Например, 1 / 2; 4 / 5. Использование основного свойства заключается в приведении исходного выражения к несократимому: 18 / 30 = 3 / 5 (после сокращения на шесть).
Нужно отметить, что на рассмотренных правилах построены практически все алгоритмы, связанные с выполнением математических действий над дробями.
Действия с дробями
Перед тем как приступить к изучению алгоритмов выполнения арифметических операций над дробями, нужно научиться преобразовывать смешанное отношение в неправильное число и находить наименьший общий знаменатель.
Для преобразования необходимо целое умножить на делитель дробной части, а затем полученное число сложить с её делимым. Затем результат прибавления занести в числитель, а знаменатель записать без изменения. При этом целое число можно представить как неправильную дробь, если добавить к ней знаменатель, равняющийся единице. Например, 9 (3 / 4) = ((9 * 4) + 3) / 4 = 39 / 4. Это операция обратимая, то есть преобразование можно выполнить и в обратную сторону.
Если в выражениях, над которыми необходимо выполнить сложение или вычитание, стоят одинаковые по значению делители, то говорят, что они приведённые. То есть чтобы выполнить арифметическую операцию, нужно найти общее кратное для всех знаменателей. Для его определения существуют несколько методов. Самый простой, но далеко не рациональный, простое перемножение делителей.
Другой заключается в выявлении наименьшего числа среди всех знаменателей, умножения его на два с последующей пробой деления полученного результата на оставшиеся делители без остатка. Если это невозможно, меньший знаменатель умножают на три. Это действие повторяют до тех пор, пока не найдётся число, делящееся на все делители без остатка.
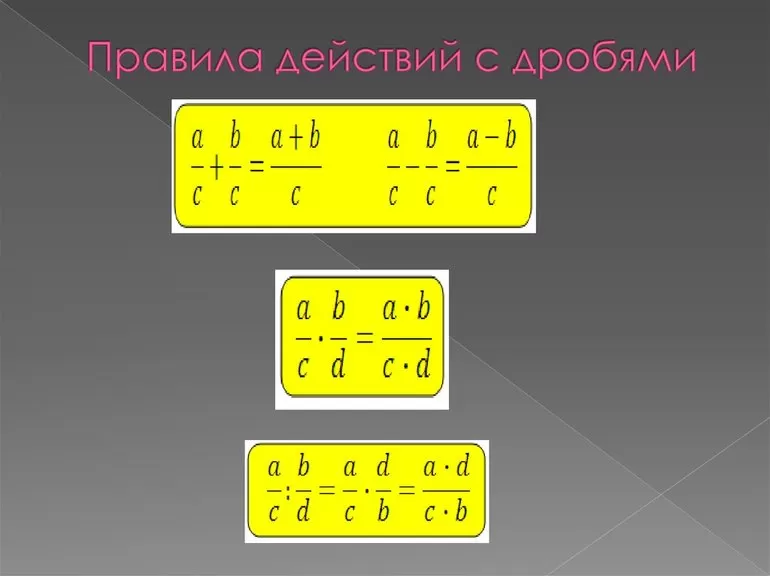
Алгоритмы выполнения операций над дробными выражениями следующие:

- Умножение. Чтобы перемножить две дроби между собой, нужно отдельно найти произведение знаменателей и числителей. Формула для этого действия выглядит так: a/b * c/d = (a * c) / (b * d).
- Деление. По сути, операция является обратной умножению. Это и используется при нахождении частного. Правило звучит следующим образом: чтобы разделить дробь на дробь, нужно первую оставить без изменения, а во второй поменять местами числитель со знаменателем, заменив при этом знак деления на умножение. Математическая формула будет следующей: (a / b): (c / d) = (a * d) / (b * c).
- Сложение. Действие совершают в несколько этапов. На первом шаге выражения приводят к общему знаменателю. На втором находят дополнительные множители для числителей путём деления найденного числа на каждый делитель. Полученный результат умножают на соответствующее значение числа в делимом. На последнем этапе складывают числители. Вычитание осуществляется аналогично.
Решение задач
Несмотря на то что свойства дробей несложны, для лучшего их понимания нужно прорешать несколько простых примеров. Обычно хватает решить около шести заданий, чтобы получить необходимые навыки. Вот несколько наиболее интересных типовых примеров для самостоятельной работы:

- Найти, какое из двух выражений больше: 3 / 5 + 12 / 16 или 2 (4/5). Чтобы выполнить сравнение, нужно найти частное для первого многочлена. Его нахождение будет выглядеть следующим образом: 3 / 5 + 12 / 16 = 3 /5 + 3 / 4 = ((3 * 4) + (3 * 5)) / 20 = (12 + 15) / 20 = 27 /20. Получилось неправильное выражение. Согласно правилу преобразования, его нужно представить, как смешанную дробь: 27 /20 = ((1 * 20) + 7) / 20 = (1 * 20) / 20 + 7 / 20 = 1 + 7 / 20 = 1 (7/20). Так как в расчёте целая часть равняется единице, а в сравниваемой — двойке, то можно утверждать, что (3 / 5 + 12 / 16) меньше 2 (4/5).
- Вычислить ответ для числового выражения: 4 / 9 * 12 / 5 + 7 / 8: 5 / 6 — 11 / 30. Решение можно разбить на несколько шагов. На первом найти произведение: 4 / 9 * 12 / 5 = (4 * 12) / (9 * 5). Это выражение можно сократить на три, в итоге получится: (4 * 4) / (3 * 5) = 16 /15. На втором шаге нужно выполнить деление: 7 / 8: 5 / 6 = (7 * 6) / (8 * 5) = (7 * 3) / (4 * 5) = 21 /20. Теперь останется сложить полученные дроби. Сделать это нужно с помощью подбора общего знаменателя: 16 / 15 + 21 / 20 — 11 / 30 = 64 / 60 + 63 / 60 — 22 / 60 = (64 + 63- 22) / 60 = 105 / 60 = 7 / 4 = 1 (¾).
- Решить пример: 6 (1/7) + 7 (2/3). Существует два способа позволяющих найти ответ. Первый заключается в обращении смешанных выражений в неправильные, а после выполнения действия сложения. Второй же подразумевает отдельное нахождение суммы целых и дробных частей. Пожалуй, проще решать следующим методом: 6 (1/7) + 7 (2/3) = 6 + (1/7) + 7 + (2/3) = (6 + 7) + (1 / 7) + (2 / 3) = 13 + (1 / 7 + 2 / 3) = 13 + (3 + 7) / 21 = 13 + 10 / 21 = 13 (10 / 21). Важно отметить, что при умножении или делении смешанных дробей всегда нужно их приводить к неправильному виду.
Таким образом, использование свойств требует логического мышления и знания формул выполнения действий.
На этапе обучения их можно даже выписать в отдельную таблицу и пользоваться ей при решении, пока действия не дойдут до автоматизма. При этом полученный результат удобно проверять на онлайн-калькуляторах, которых в интернете можно насчитать более двух десятков. Это обычные сайты, выполняющие различные расчёты в режиме реального времени.
Источник
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Источник
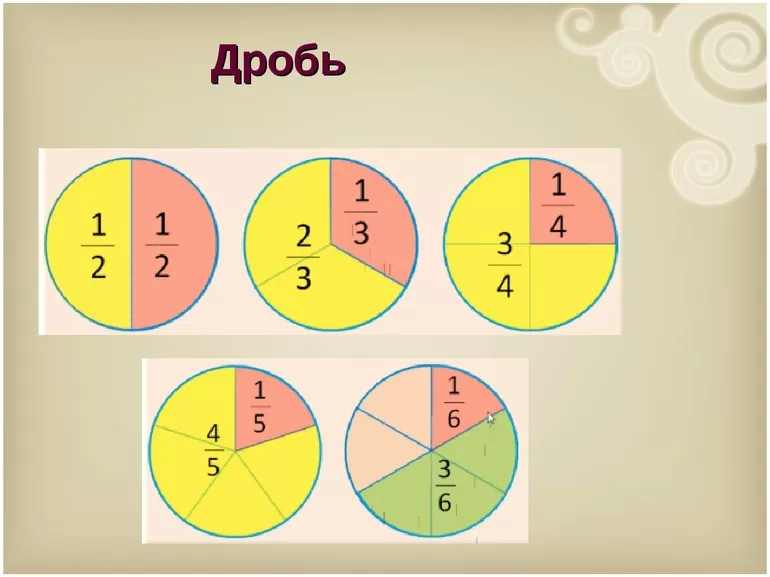
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Виды дробей:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 – 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x – y). Значение дроби зависит от данных значений букв.
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Запомнить все определения и решать задачки без труда помогут в современной онлайн-школе Skysmart. Ученики занимаются на интерактивной платформе с красочными героями, отслеживают прогресс в личном кабинете и получают поддержку внимательных учителей.
Запишите ребенка на бесплатный вводный урок и начните заниматься математикой в удовольствие уже завтра!
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делимое — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
где a, b, k — натуральные числа.
- Дробь не имеет значения, при условии, если делитель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4
- Поэтому первая дробь 1/5 меньше второй 4/5.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Как рассуждаем:
- Приведем дроби к общему знаменателю:
- Сравним дроби с одинаковыми знаменателями:
Ответ: 2/7 > 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю (НОЗ);
- сравнить полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
- Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
- Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
- Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
- Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
Приходите тренироваться в Skysmart! Разберемся в самой коварной теме и подтянем оценки по математике в школе.
Источник
