Какие свойства характеризуют осевые и полярные моменты инерции площади сечения
Сопротивление материалов
При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения.
Самый простой пример – обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда – решающее) не только величина площади сечения бруса, но и его геометрическая форма.
При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).
Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими.
Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы – чем больше плечо силы – тем больше ее момент (относительно оси или точки). Аналогично – чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).
***
Статический момент площади
Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (Si) на расстояния (ri)от них до этой оси.
Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:
- разбить фигуру на крохотные (элементарные) площадки (рис. 1);
- умножить площадь каждой площадки на расстояние ri от ее центра до рассматриваемой оси;
- сложить полученные результаты.
Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: Sx, Sy, Sz.
Примечание: в разных учебниках или других источниках информации обозначение тех или иных физических величин может отличаться от приведенных на этом сайте. Как вы понимаете, от условного обозначения величин суть описываемых явлений и закономерностей не изменяется.
Sx = Σ y dA; Sy = Σ x dA.
Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.
Из этого вывода следует еще один вывод – если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.
Единица измерения статического момента площади – метр кубический (м3).
При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части – прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов.
***
Полярный момент инерции
Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (Si) этой фигуры на квадрат их расстояний (r2i) до полюса.
Полярный момент инерции обозначают Iρ (иногда его обозначают Jρ), а формула для его определения записывается так:
Iρ = Σ ρ2 dA.
Единица измерений полярного момента инерции – м4, из чего следует, что он не может быть отрицательным.
Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.
Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение.
***
Осевой момент инерции
Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис).
Осевой момент инерции обозначается I (иногда – J)с индексом, соответствующим оси:
Ix = Σ y2 dA; Iy = Σ x2 dA.
Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫.
Очевидно, что осевой и полярный момент инерции выражаются в одинаковых единицах – м4. Осевой момент инерции величина всегда положительная и не равна нулю (м4 не может быть отрицательным, а площадь не может быть равной нулю, иначе пропадает и сама фигура, как площадка).
Если сложить осевые моменты инерции плоской фигуры относительно перпендикулярных осей, то получим полярный момент инерции этой фигуры относительно точки пересечения этих осей (начала координат), т. е. :
Ix + Iy = Iρ.
Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру.
Понятие осевого момента инерции понадобится при изучении теории изгиба.
Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:
Для прямоугольника размером b × h: | Ix = bh3 /12 | ||
Для квадрата со стороной а: | Ix = a4 / 12 | ||
Для круга диаметром d: | Ix = Iy≈ 0,05 d4 | ||
Для кольцевого сечения размером D × d: | Ix = Iy≈ 0,05 (D4 – d4) |
***
Момент инерции при параллельном переносе осей
Оси, проходящие через центр тяжести плоской фигуры, называют центральными осями.
Момент инерции относительно центральной оси называется центральным моментом инерции.
Теорема
Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади фигуры на квадрат расстояния между осями.
Для доказательства этой теоремы рассмотрим произвольную плоскую фигуру, площадь которой равна А, центр тяжести расположен в точке С, а центральный момент инерции относительно оси x будет Ix.
Вычислим момент инерции фигуры относительно некоторой оси x1, параллельной центральной оси и отстоящей от нее на расстоянии а (рис. 2).
Ix1 = Σ y12 dA + Σ (y + a)2 dA =
= Σ y2 dA + 2a Σ y dA + a2 Σ dA.
Анализируя полученную формулу, отмечаем, что первое слагаемое – осевой момент инерции относительно центральной оси, второе слагаемое – статический момент площади этой фигуры относительно центральной оси (следовательно, он равен нулю), а третье слагаемое после интегрирования может быть представлено в виде произведения a2 A, т. е. в результате получим формулу:
Ix1 = Ix + а2 А – теорема доказана.
На основании теоремы можно сделать вывод, что из ряда параллельных осей осевой момент инерции плоской фигуры будет наименьшим относительно центральной оси.
***
Главные оси и главные моменты инерции
Представим себе плоскую фигуру, моменты инерции которой относительно осей координат Ixи Iy, а полярный момент инерции относительно начала координат равен Iρ. Как было установлено ранее,
Ix + Iy = Iρ.
Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты будут изменяться, при этом их сумма останется величиной постоянной. Поскольку сумма переменных величин постоянна, то одна из них уменьшается, а другая увеличивается, и наоборот.
Следовательно, при определенном положении осей один из осевых моментов достигнет максимального значения, а другой – минимального.
Оси, относительно которых моменты инерции имеют минимальное и максимальное значения, называют главными осями инерции.
Момент инерции относительно главной оси называется главным моментом инерции.
Если главная ось проходит через центр тяжести фигуры, она называется главной центральной осью, а момент инерции относительно такой оси – главным центральным моментом инерции.
Можно сделать вывод, что если фигура симметрична относительно какой-нибудь оси, то эта ось всегда будет одной из главных центральных осей инерции этой фигуры.
***
Центробежный момент инерции
Центробежным моментом инерции плоской фигуры называют взятую по всей площади сумму произведений элементарных площадок на расстояние до двух взаимно перпендикулярных осей:
Ixy = Σ xy dA,
где x, y – расстояния от площадки dA до осей x и y.
Центробежный момент инерции может быть положительным, отрицательным и равным нулю.
Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений.
В таблицах стандартных профилей содержится характеристика, которая называется радиусом инерции сечения, вычисляемая по формулам:
ix = √ (Ix / A), iy = √ (Iy / A), (здесь и далее знак “√” – знак корня)
где Ix, Iy – осевые моменты инерции сечения относительно центральных осей; А – площадь сечения.
Эта геометрическая характеристика используется при изучении внецентрального растяжения или сжатия, а также продольного изгиба.
***
Материалы раздела “Сопротивление материалов”:
- Основные понятия и определения
- Растяжение и сжатие
- Смятие. Контактные напряжения
- Деформация сдвига (среза)
- Деформация кручения
- Деформация изгиба
Растяжение и сжатие
Правильные ответы на вопросы Теста № 2
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 2 | 3 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 2 |
Источник
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
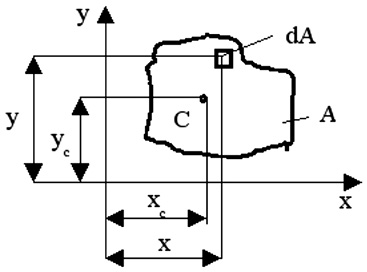
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
(3)
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
(4)
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
(5)
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
Полярный момент сопротивления
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
По аналогии запишем
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца . Подставляя выражение для
площади кольца в выражение для Jρ и интегрируя, получим:
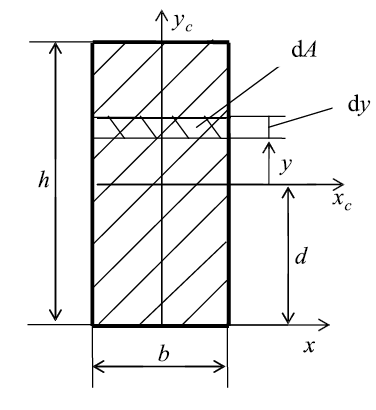
Рис. 11. Прямоугольник
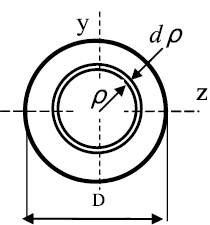
Рис. 12. Круг
Тогда
Источник
В дальнейшем в
расчетах на прочность мы будем встречаться
еще с некоторыми геометрическими
характеристиками сечений. Это так
называемые моменты инерции сечений.
Различают полярные и осевые моменты
инерции.
Полярным моментом
инерции сечения называется взятая по
всему сечению сумма произведений или
интеграл элементарных площадей на
квадраты их расстояний до некоторой
точки О сечения.
Jp
=
Для поперечных
сечений в форме круга или кругового
кольца полярный момент инерции
характеризует способность сопротивляться
кручению и используется как геометрическая
характеристика поперечного сечения
при расчетах на кручение.
Полярный момент инерции измеряется в
единицах длины в четвертой степени
(см4,
мм4,
м4).
Практический
интерес представляет полярный момент
инерции относительно центра тяжести
сечения.
Величина
полярного момента инерции круга
определяется по
следующей формуле
Jр
= πd4/32,
или
приближенно Jр0,1
d4
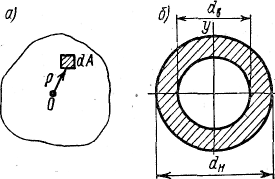
Полярный
момент инерции кольца равен разности
полярных моментов
инерции двух кругов диаметрами dн
и
dв
Jр
= (πd4
н/32)(1-α4)
,
где
α= dв
/dн
Приближенно
для кольца Jр
= 0,1d4(1—
α4)
Осевым
моментом инерции сечения называется
взятая по всему сечению
сумма произведений или интеграл
элементарных площадок на
квадраты их расстояний до некоторой
оси, лежащей в плоскости рассматриваемого
сечения.
Так,
относительно осей х
и
у
(рис.в)
осевые моменты инерции определяются
следующими выражениями:
Jx
=;
Jy
=.
Величина
осевого момента инерции служит
характеристикой способности
балки сопротивляться изгибу.
Осевые моменты инерции,
так же как полярные, всегда положительны
и измеряются в
единицах длины в четвертой степени
(см4,
мм4,
м4).
В
практических расчетах наибольший
интерес представляют моменты
инерции относительно так называемых
главных осей, проходящих
через центр тяжести сечения. В дальнейшем
будем рассматривать
только сечения, имеющие не менее одной
оси симметрии.
Относительно
одной из главных центральных осей момент
инерции
имеет наибольшее из всех возможных
значений, а относительно другой —
наименьшее. Ось симметрии сечения всегда
является
одной из главных центральных осей, а
другая главная центральная
ось ей перпендикулярна. В дальнейшем
рассматриваются
сечения, обладающие симметрией, что
позволяет легко определять
их главные центральные оси.
Для
прямоугольного сечения (рис. а)
осевой
момент инерции
определяется по формуле: Jx
=bh3/12.
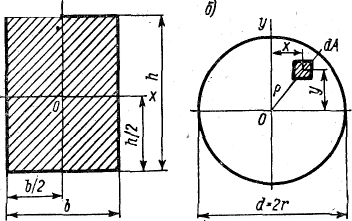
Для
круга моменты инерции относительно
любых осей, проходящих
через его центр, равны между собой, т.е.
Jx
=Jyпоэтому
Jx
=Jy=
= πd4/640,05
d4
Аналогично
для кольцевого сечения Jx
=Jy=
(πd4
н/54)(1-α4)
где
α= dв
/dн
Осевые
моменты инерции относительно
параллельных осей
Для
вычисления осевых моментов инерции
сложных сечений часто
приходится пользоваться теоремой о
моментах инерции относительно
параллельных осей.
Момент
инерции сечения относительно
оси, не проходящей через его центр
тяжести, равен сумме момента
инерции сечения относительно его
центральной оси, параллельной
данной оси, и произведения площади
сечения на
квадрат расстояния между осями.
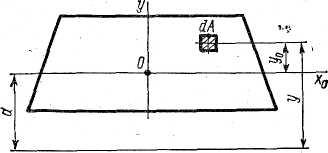
Обозначим
у
расстояние
элементарной
площадки а
от
оси х,
а
yо
— расстояние
от параллельной ей центральной
оси х;
расстояние
между осями обозначим aочевидно,
что
у=
yо
+ а.
Момент
инерции
рассматриваемого сечения относительно
оси х
Jx
= Jx+Aa2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
08.03.201514.37 Mб12Конспект лекций по ИУРЭ ДВОРСОН.doc
- #
- #
- #
- #
- #
- #
- #
- #
Источник
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ.
Как показывает опыт, сопротивление стержня различным
деформациям зависит не только от размеров поперечного сечения, но и от формы.
Размеры поперечного
сечения и форма характеризуются различными геометрическими характеристиками:
площадь поперечного сечения, статические моменты, моменты инерции, моменты
сопротивления и др.
1.
Статический момент площади (момент инерции первой степени).
Статический моментом инерции площади относительно
какой-либо оси, называется сумма произведений элементарных площадок на
расстояние до этой оси, распространенная на всю площадь (рис. 1)
 |
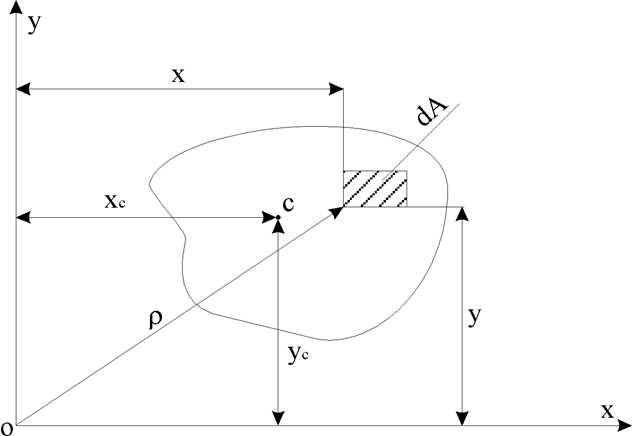Рис.1
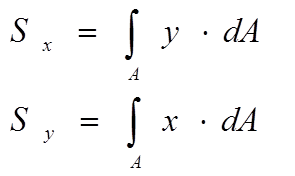
Свойства статического
момента площади:
1.
Статический момент площади
измеряется в единицах длинны третьей степени (например, см3 ).
2.
Статический момент может быть
меньше нуля, больше нуля и, следовательно, равняться нулю. Оси, относительно
которых статический момент равен нулю, проходят через центр тяжести сечения и
называются центральными осями.
Если
xcиyc –
координаты цента тяжести, то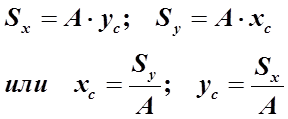 
3. Статический
момент инерции сложного сечения относительно какой-либо оси равен сумме
статических моментов составляющих простых сечений относительно той же оси.
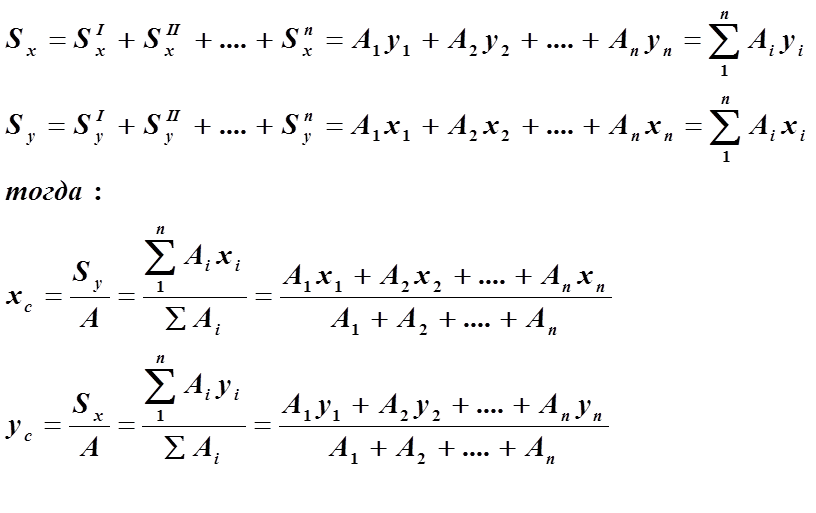
Понятие статического момента инерции в науке о
прочности используется для определения положения центра тяжести сечений, хотя
надо помнить, что в симметричных сечениях центр тяжести лежит на пересечении
осей симметрии.
2.
Момент инерции плоских сечений (
фигур ) (моменты инерции второй степени).
а) осевой
(экваториальный) момент инерции.
Осевым моментом инерции площади фигуры
относительно какой-либо оси называется сумма произведений элементарных площадок
на квадрат расстояния до этой оси распространения на всю площадь (рис. 1 )
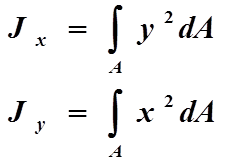
Свойства осевого момента инерции.
1.
Осевой момент инерции площади
измеряется в единицах длинны четвертой степени (например, см4 ).
2.
Осевой момент инерции всегда
больше нуля.
3.
Осевой момент инерции сложного
сечения относительно какой-либо оси равен сумме осевых моментов составляющих
простых сечений относительно той же оси:
4.
Величина осевого момента инерции
характеризует способность стержня (бруса) определенного поперечного сечения
сопротивляться изгибу.
б)
Полярный момент инерции.
Полярным
моментом инерции площади фигуры относительно какого-либо полюса называется
сумма произведений элементарных площадок на квадрат расстояния до полюса,
распространенная на всю площадь (рис. 1).
Свойства полярного момента
инерции:
1.
Полярный момент инерции площади
измеряется в единицах длины четвертой степени ( например, см4 ).
2.
Полярный момент инерции всегда
больше нуля.
3.
Полярный момент инерции сложного
сечения относительно какого-либо полюса (центра) равен сумме полярных моментов
составляющих простых сечений относительно этого полюса.
4.
Полярный момент инерции сечения
равен сумме осевых моментов инерции этого сечения относительно двух взаимно
перпендикулярных осей, проходящих через полюс.
5.
Величина полярного момента инерции
характеризует способность стержня (бруса) определенной формы поперечного
сечения сопротивляться кручению.
в)
Центробежный момент инерции.
ЦЕНТРОБЕЖНЫМ МОМЕНТОМ ИНЕРЦИИ площади фигуры относительно какой-либо системы
координат называется сумма произведений элементарных площадок на координаты,
распространенная на всю площадь (рис. 1)
Свойства центробежного момента инерции:
1.
Центробежный момент инерции
площади измеряется в единицах длинны четвертой степени (например, см4).
2.
Центробежный момент инерции может
быть больше нуля, меньше нуля, и равняться нулю. Оси, относительно которых
центробежный момент инерции равен нулю, называются главными осями инерции. Две
взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии,
будут главными осями. Главные оси, проходящие через центр тяжести площади,
называются главными центральными осями, а осевые моменты инерции площади –
главными центральными моментами инерции.
3.
Центробежный момент инерции
сложного сечения в какой-либо системе координат равен сумме центробежных
моментов инерции составляющих фигур в той же схеме координат.
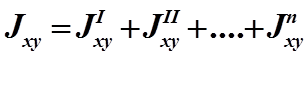
МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ.
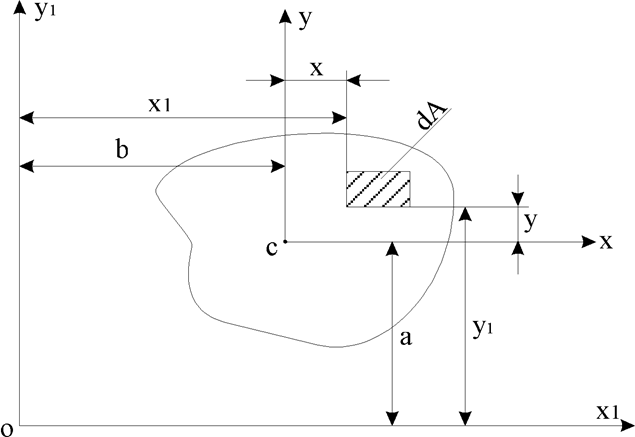Рис.2
Дано:
оси x, y – центральные;
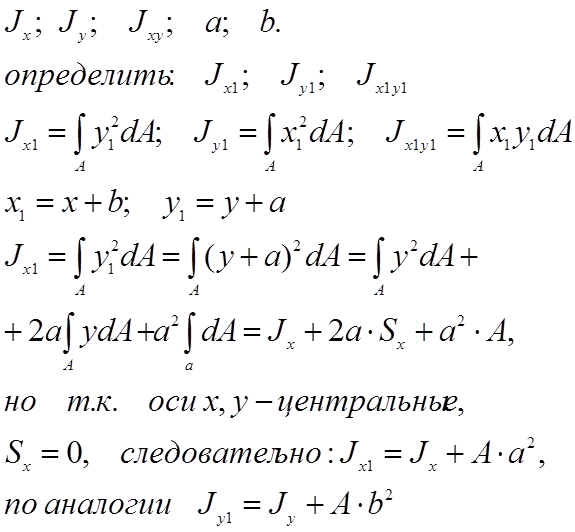
т.е. осевой момент инерции в
сечении относительно оси, параллельной центральной, равен осевому моменту
относительно своей центральной оси плюс произведение площади на квадрат
расстояния между осями. Отсюда следует, что осевой момент инерции сечения
относительно центральной оси имеет минимальную величину в системе параллельных
осей.
Сделав аналогичные выкладки
для центробежного момента инерции, получим:
Jx1y1=Jxy+Aab
т.е. центробежный момент инерции сечения относительно
осей, параллельных центральной системе координат, равен центробежному моменту в
центральной системе координат плюс произведение площади на расстояние между
осями.
МОМЕНТЫ ИНЕРЦИИ
В ПОВЕРНУТОЙ СИСТЕМЕ КООРДИНАТ
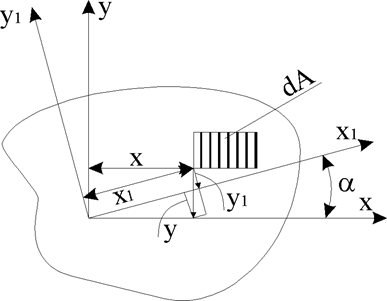
Рис. 3
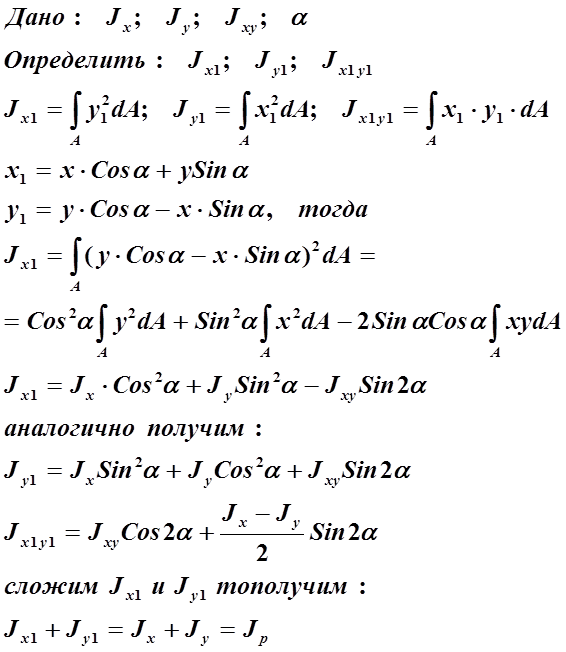
т.е. сумма осевых моментов инерции сечения есть величина
постоянная, не зависит от угла поворота осей координат и равна полярному
моменту инерции относительно начала координат. Центробежный момент инерции
может менять свою величину и обращаться в «0».
Оси, относительно которых центробежный момент равен нулю будут главными осями
инерции, а если они проходят через центр тяжести, то они называются главными
осями инерции и обозначаются «u» и «».
Моменты инерции относительно главных центральных осей
называются главными центральными моментами инерции и обозначаются , причем главные центральные моменты
инерции имеют экстремальные значения, т.е. один «min», а другой «max».
Пусть угол «a0»
характеризует положение главных осей, тогда:
по этой зависимости
определяем положение главных осей. Величину же главных моментов инерции после
некоторых преобразований, определяем по следующей зависимости:
ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ОСЕВЫХ МОМЕНТОВ ИНЕРЦИИ, ПОЛЯРНЫХ
МОМЕНТОВ ИНЕРЦИИ И МОМЕНТОВ СОПРОТИВЛЕНИЯ ПРОСТЕЙШИХ ФИГУР.
1.
Прямоугольное сечение
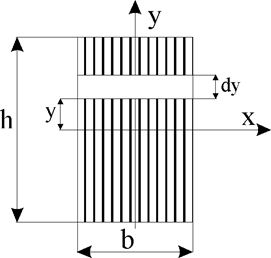
Рис.4
Оси x и y –
здесь и в других примерах – главные центральные оси инерции.
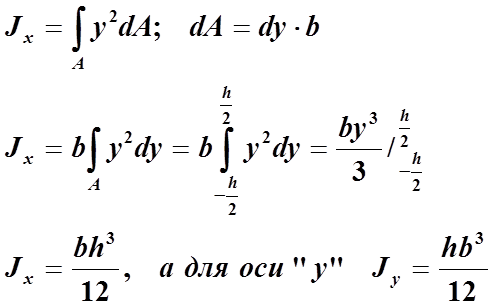
Определим осевые моменты
сопротивления:
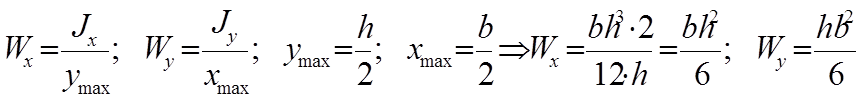
2.
Круглое сплошное сечение. Моменты
инерции.
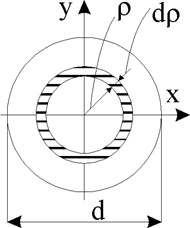
Рис.5
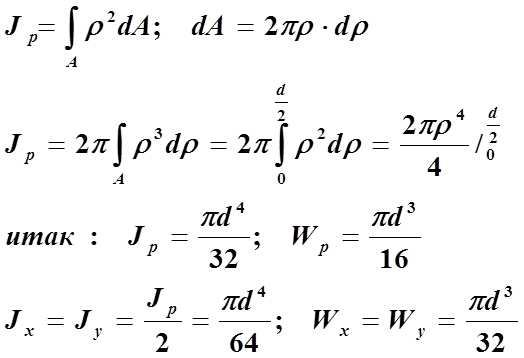
3.
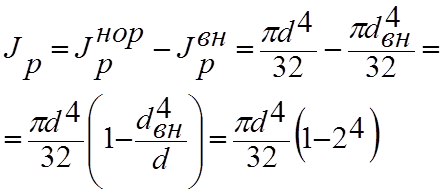
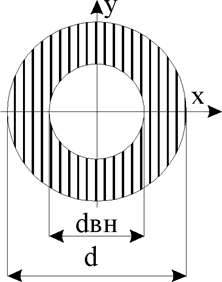Кольцевое сечение.
Рис.6
 |
 |
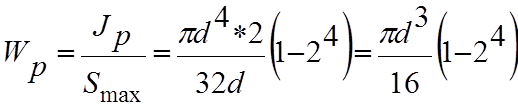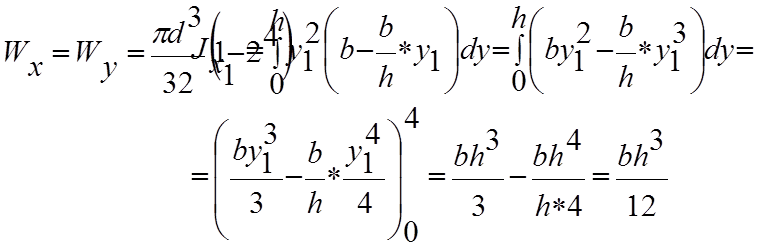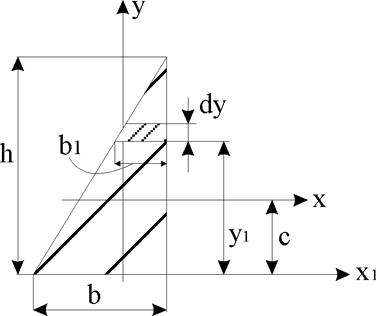
4.Треугольник
 |
 |
 |
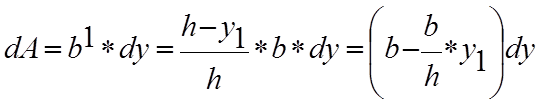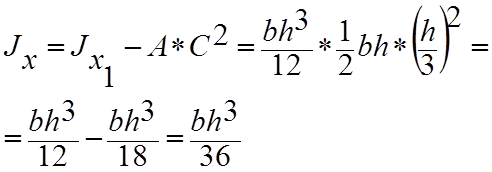Источник