Какие свойства характеризуют сопротивление материала деформации

Сопротивление деформации
Напряжение, вызывающее пластическую деформацию материала при данных
термомеханических условиях деформирования и линейном напряженном состоянии называется сопротивлением
деформации.
Сопротивление металла деформации определяется делением усилия на текущую
площадь сечения образца при деформировании:
σ=P/F
Сопротивление металла деформации является реологической характеристикой.
Реология рассматривает внутренние изменения в металле, определяющие связь напряжения со степенью
и скоростью деформации.
Теоретические и экспериментальные исследования зависимости сопротивления
деформации от различных технологических параметров имеют большое практическое значение при
разработке процессов обработки металлов давлением. В обработке металлов давлением знание сопротивления
деформации необходимо для определения энергосиловых параметров прокатки и проверки оборудования
на прочность. Кроме того, сопротивления деформации можно использовать и для оценки свойств
металла, получаемых после пластической деформации. Это особенно важно при термомеханической
обработке, где получение требуемого комплекса механических свойств является основной задачей.
Многочисленными исследованиями российских [1001]
[1015, 1055,
1044, 362]
и зарубежных [363, 1098]
авторов установлено, что сопротивление деформации зависит от природы деформируемого тела,
предшествовавшей обработки, вида напряженного состояния, температуры и скорости деформации,
физико-химических изменений, происходящих в процессе деформирования, и ряда других факторов.
Большое число определяющих параметров, а также сложность их совместного влияния являются основной
трудностью на пути создания аналитических выражений для определения сопротивления деформации.
На основании результатов исследований предложен ряд формул, отражающих
влияние того или иного фактора на сопротивление деформации и представляющих собой полиномы,
показательные, экспоненциальные, логарифмические и другие виды функций. Область их применения
ограничена условиями проведения экспериментов, на основании которых были получены входящие
в них коэффициенты. Поэтому нет необходимости подробно останавливаться на их анализе.
В работе [367] отмечено,
что распространенный способ выражения связи деформаций ε и напряжений σ в виде σ=f(ε)
является неточным, поскольку в этом случае учитывается только вертикальная составляющая деформации.
Указанная зависимость справедлива лишь для случая линейного напряженного состояния.
Теория обработки металлов давлением располагает многочисленными зависимостями,
учитывающими влияние нескольких технологических факторов на сопротивление деформации, позволяющими
с той или иной погрешностью рассчитать силовые условия прокатки [1055].
Вместе с тем, эти формулы не всегда правильно отражают зависимость сопротивления деформации
от всего многообразия технологических параметров, а поэтому их использование приводит к большим ошибкам.
Предложено много формул, устанавливающих зависимость сопротивления деформации
от различных влияющих факторов (температуры, скорости и степени деформации). Например, с использованием
термомеханических коэффициентов В.И. Зюзина, Л.В.
Андреюка – Г.Г. Тюленева [1018], по
химическому составу [1078]. Однако
они не отражают в достаточной мере влияния тех или иных параметров процесса деформирования.
В частности, “история нагружения” учитывается лишь в теории наследственности [1099].
При прокатке, особенно с применением высокотемпературной термомеханической
обработки, рассчитать сопротивление деформации металла после деформирования и охлаждения и
таким образом характеризовать полученные свойства невозможно без надежных формул, учитывающих
изменяющиеся во времени в широких пределах температуру, скорость и степень деформации.
Пример экранной формы.
Ссылка “Возврат на один уровень вверх” осуществляет переход на предыдущую страницу.
Источник
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
Тут может возникнуть вопрос: почему нельзя просто определить сопротивление материала? Дело в том, что абсолютно упругие материалы, разрушающиеся только после преодоления некоторого предела – сопротивления, существуют только в теории. В реальности большинство материалов обладают как упругими так и пластическими свойствами, что это за свойства, рассмотрим ниже на примере металлов.
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
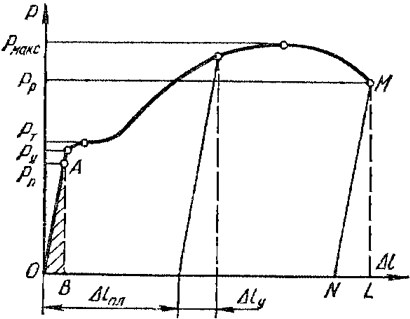
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
σп = Рп/Fo (318.2.1)
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
где k – коэффициент жесткости:
k = EF/l (318.2.3)
где l – длина образца, F – площадь сечения, Е – модуль Юнга.
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
а относительное удлинение ε – отношению абсолютной деформации к начальной длине
εпр = Δl/lo (318.3.2)
то модуль Юнга согласно закону Гука можно выразить так
Е = σ/εпр = Plo/FoΔl = tgα (318.3.3)
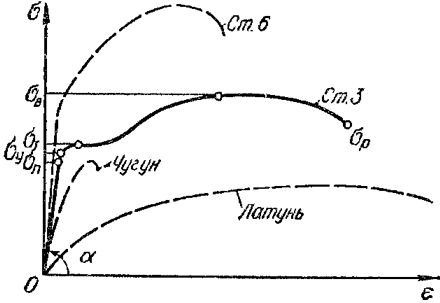
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
εпоп = Δd/do (318.3.4)
Тогда коэффициент Пуассона можно выразить следующим уравнением:
μ = εпоп/εпр (318.3.5)
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
При угловых деформациях рассматриваемое сечение перемещается не линейно, а под некоторым углом – углом сдвига γ к начальному сечению. Так как касательные напряжения равны силе, деленной на площадь в плоскости которой действует сила:
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
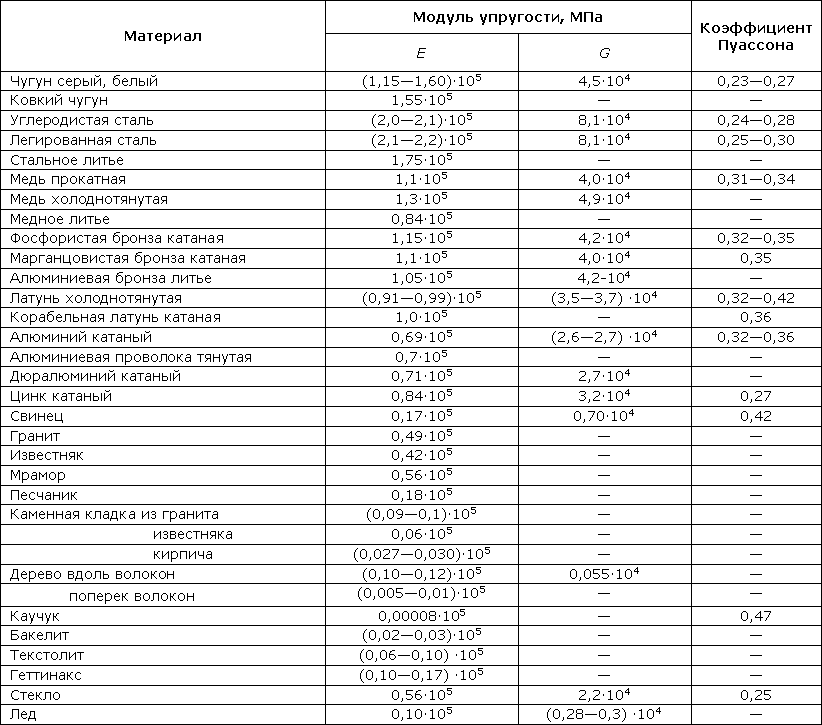
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
σу = Ру/Fo (318.2.4)
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
3. Предел текучести Рт
σт = Рт/Fo (318.2.5)
Ограничивает участок диаграммы на котором деформация увеличивается без значительного увеличения нагрузки (состояние текучести). При этом по всему объему образца происходит частичный разрыв внутренних связей, что и проводит к значительным пластическим деформациям. Материал образца полностью не разрушается, но его начальные геометрические размеры претерпевают необратимые изменения. На отшлифованной поверхности образцов наблюдаются фигуры текучести – линии сдвигов (открытые профессором В. Д. Черновым). Для различных металлов углы наклона этих линий различны, но находятся в пределах 40-50о. При этом часть накопленной потенциальной энергии необратимо расходуется на частичный разрыв внутренних связей. При испытании на растяжение принято различать верхний и нижний пределы текучести – соответственно наибольшее и наименьшее из напряжений, при которых возрастает пластическая (остаточная) деформация при почти постоянной величине действующей нагрузки.
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
σв = Рмакс/Fo (318.2.6)
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
В таблицах 318.2 – 318.5 приведены ориентировочные величины пределов прочности для некоторых материалов:
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
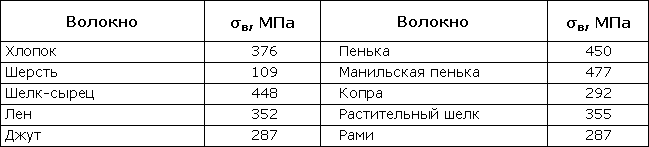
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород
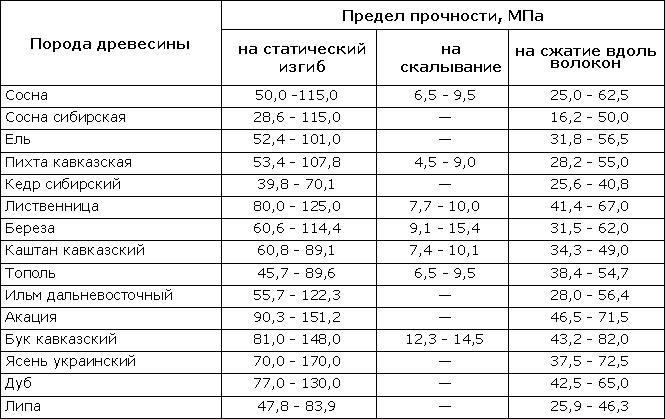
5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования “шейки” значительно изменяется площадь сечения образца в районе “шейки”. Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
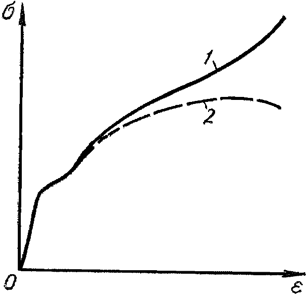
Рисунок 318.3. Диаграмма напряжений: 2 – по отношению к начальной площади поперечного сечения, 1 – по отношению к изменяющейся площади сечения в районе шейки.
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
ψ = 100(Fo – F)/Fo (318.2.7)
где Fo – начальная площадь поперечного сечения образца (площадь поперечного сечения до деформации), F – площадь поперечного сечения в районе “шейки”. Чем больше значение ψ, тем более ярко выражены пластические свойства материала. Чем меньше значение ψ, тем больше хрупкость материала.
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
где 1/2 – результат статического действия нагрузки, возрастающей от 0 до Р в момент ее приложения (среднее значение (0 + Р)/2)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
где η – коэффициент полноты диаграммы, равный отношению площади всей диаграммы, ограниченной кривой АМ и прямыми ОА, MN и ON, к площади прямоугольника со сторонами 0Рмакс (по оси Р) и Δlмакс (пунктир на рис. 318.1). При этом надо вычесть работу, определяемую площадью треугольника MNL (относящуюся к упругим деформациям).
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5
а – для пластических материалов; б – для хрупких материалов ; в – для дерева вдоль волокон, г – для дерева поперек волокон.
Испытания на сжатие менее удобны для определения механических свойств пластических материалов из-за трудности фиксирования момента разрушения. Методы механических испытаний металлов регламентируются ГОСТ 25.503-97. При испытании на сжатие формы образца и его размеры могут быть различными. Ориентировочные значения пределов прочности для различных материалов приведены в таблицах 318.2 – 318.5.
Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.
Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.
Влияние температуры на изменение механических свойств материалов
Твердое состояние – не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.
Таблица 318.6. Температуры плавления некоторых веществ
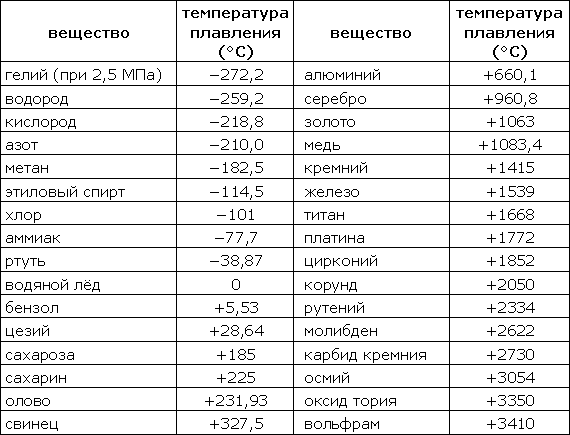
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.
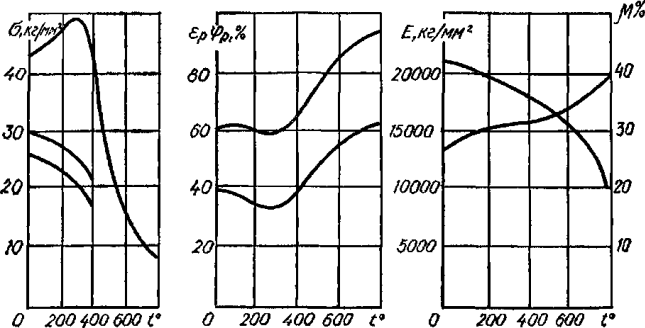
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия – увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Облучение пластмасс также приводит к увеличению хрупкости, причем на предел прочности этих материалов облучение оказывает различное влияние: на некоторых пластмассах оно почти не сказывается (полиэтилен), у других вызывает значительное понижение предела прочности (катамен), а в третьих – повышение предела прочности (селектрон).
Источник
