Какие свойства имеет прямоугольный треугольник
Онлайн всего: 1
Гостей: 1
Пользователей:
Стандартные обозначения в прямоугольных треугольниках
Определение. Прямоугольный треугольник – треугольник, один из углов которого прямой (равен ).
Прямоугольный треугольник – частный случай обычного треугольника. Поэтому все свойства обычных треугольников для прямоугольных сохраняются. Но есть и некоторые частные свойства, обусловленные наличием прямого угла.
Общепринятые обозначения (рис.1):
– прямой угол;
– гипотенуза;
– катеты;
.
Рис. 1.
Свойства прямоугольного треугольника.
Свойство 1. Сумма углов и прямоугольного треугольника равна .
Доказательство. Вспомним, что сумма углов любого треугольника равна . Учитывая тот факт, что , получаем, что сумма оставшихся двух углов равна То есть,
Свойства прямоугольного треугольника (сумма острых углов, соотношение длин катетов и гипотенузы, неравенство треугольника)
Свойство 2. В прямоугольном треугольнике гипотенуза больше любого из катетов (является самой большой стороной).
Доказательство. Вспомним, что в треугольнике против большего угла лежит большая сторона (и наоборот). Из доказанного выше свойства 1 следует, что сумма углов и прямоугольного треугольника равна . Так как угол треугольника не может равняться 0, то каждый из них меньше . Значит, является самым большим, а, значит, напротив него лежит наибольшая сторона треугольника. Значит, гипотенуза является наибольшей стороной прямоугольного треугольника, то есть: .
Свойство 3. В прямоугольном треугольнике гипотенуза меньше суммы катетов.
Доказательство. Это свойство становится очевидным, если вспомнить неравенство треугольника.
Неравенство треугольника
В любом треугольнике сумма любых двух сторон больше третьей стороны.
Из данного неравенства сразу же следует свойство 3.
Примечание: несмотря на то, что каждый из катетов по отдельности меньше гипотенузы, их сумма оказывается больше. В числовом примере это выглядит так: , но .
Признаки равенства прямоугольных треугольников:
1-й признак (по 2 сторонам и углу между ними): если у треугольников равны две стороны и угол между ними, то такие треугольники равны между собой.
2-й признак (по стороне и двум прилежащим углам): если у треугольников равны сторона и два угла, прилежащие к данной стороне, то такие треугольники равны между собой.Примечание: пользуясь тем, что сумма углов треугольника постоянна и равна , легко доказать, что условие «прилежания» углов не является необходимым, то есть признак будет верен и в такой формулировке: «… равны сторона и два угла, то …».
3-й признак (по 3 сторонам): если у треугольников равны все три стороны, то такие треугольники равны между собой.
Естественно, все эти признаки остаются верными и для прямоугольных треугольников. Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются. Итак, сформулируем признаки равенства прямоугольных треугольников:
1-й признак (по двум катетам): если у прямоугольных треугольников катеты попарно равны, то такие треугольники равны между собой (Рис. 2).
Дано:
Рис. 2. Иллюстрация первого признака равенства прямоугольных треугольников
Доказать:
Доказательство: в прямоугольных треугольниках: . Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: .
2-й признак (по катету и углу): если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 3).
Дано:
Рис. 3. Иллюстрация второго признака равенства прямоугольных треугольников
Доказать:
Доказательство: сразу отметим, что тот факт, что равны углы, прилежащие к равным катетам, не является принципиальным. Действительно, сумма острых углов прямоугольного треугольника (по свойству 1) равна . Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).
Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов . Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: .
3-й признак (по гипотенузе и углу): если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 4).
Дано:
Рис. 4. Иллюстрация третьего признака равенства прямоугольных треугольников
Доказать:
Доказательство: для доказательства этого признака можно сразу воспользоваться вторым признаком равенства треугольников – по стороне и двум углам (точнее, следствием, в котором указано, что углы не обязательно должны быть прилежащими к стороне). Действительно, по условию: , , а из свойств прямоугольных треугольников следует, что . Значит, мы можем воспользоваться вторым признаком равенства треугольников, и получить: .
4-й признак (по гипотенузе и катету): если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны между собой (Рис. 5).
Дано:
Рис. 5. Иллюстрация четвёртого признака равенства прямоугольных треугольников
Доказать:
Доказательство: для доказательства этого признака воспользуемся признаком равенства треугольников, который мы сформулировали и доказали на прошлом уроке, а именно: если у треугольников равны две стороны и больший угол, то такие треугольники являются равными. Действительно, по условию у нас есть две равных стороны. Кроме того, по свойству прямоугольных треугольников: . Осталось доказать, что прямой угол является наибольшим в треугольнике. Предположим, что это не так, значит, должен быть ещё хотя бы один угол, который больше . Но тогда сумма углов треугольника уже будет больше . Но это невозможно, значит, такого угла в треугольнике быть не может. Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить: .
Сформулируем теперь ещё одно свойство, характерное только для прямоугольных треугольников.
Свойство
Катет, лежащий против угла в , в 2 раза меньше гипотенузы (Рис. 6).
Дано:
Рис. 6.
Доказать: AB
Доказательство: выполним дополнительное построение: продлим прямую за точку на отрезок, равный . Получим точку . Так как углы и – смежные, то их сумма равна . Поскольку , то и угол .
Значит, прямоугольные треугольники (по двум катетам: – общий, – по построению) – первый признак равенства прямоугольных треугольников.
Из равенства треугольников следует равенство всех соответствующих элементов. Значит, . Откуда: . Кроме того, (из равенства всё тех же треугольников). Значит, треугольник – равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен , – равносторонний. Из этого следует, в частности, что .
Свойство катета, лежащего против угла в
Стоит отметить, что верно и обратное утверждение: если в прямоугольном треугольнике гипотенуза в два раза больше одного из катетов, то острый угол, лежащий напротив этого катета, равен .
Примечание: признак означает, что если какое-то утверждение верно, то треугольник является прямоугольным. То есть признак позволяет идентифицировать прямоугольный треугольник.
Важно не путать признак со свойством – то есть, если треугольник прямоугольный, то у него есть такие свойства… Часто признаки и свойства являются взаимно обратными, но далеко не всегда. Например, свойство равностороннего треугольника: в равностороннем треугольнике есть угол . Но это не будет признаком равностороннего треугольника, так как не любой треугольник, у которого есть угол , является равносторонним.
Можно привести и более жизненный пример: свойство слова «хлеб» – в слове «хлеб» 4 буквы. Но наличие 4 букв не является признаком слова «хлеб», так как существует множество слов из 4 букв.
Признак прямоугольного треугольника (медиана равна половине стороны, к которой проведена)
Признак прямоугольного треугольника:
Если в треугольнике медиана равна половине стороны, к которой она проведена, то данный треугольник является прямоугольным, причём медиана проведена из вершины прямого угла.
Примечание: медиана – линия, соединяющая вершину треугольника с серединой противоположной стороны (Рис. 7).
Дано:
Рис. 7.
Доказать:
Доказательство: поскольку , то – равнобедренные. Значит, углы при основаниях каждого из этих треугольников равны. То есть, , . Тогда сумма углов треугольника равна Значит, . Но: .
Теорема Пифагора: .
Решение прямоугольного треугольника:
;
;
.
Теоремы:
- Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу: .
- Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на два подобных и подобных исходному треугольнику. Для любых сходственных элементов (медиана, биссектриса, радиусы вписанной и описанной окружностей и т. п.) исходного и полученных треугольников справедливо соотношение .
- Длина высоты, проведенной из вершины прямого угла, равна отношению произведения длин катетов и гипотенузы: .
- Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы: .
- Радиус вписанной окружности равен половине суммы катетов, уменьшенной на гипотенузы:
Источник
Прямоугольный треугольник выделяется на фоне остальных треугольников. Прямой угол наделяет его целым рядом специфических свойств. Разберемся, какими именно свойствами обладает прямоугольный треугольник и почему.

Что такое прямоугольный треугольник?
Прямоугольный треугольник – это треугольник, содержащий прямой угол.
Сторона, лежащая напротив прямого угла, зовется гипотенузой, две другие стороны всегда называются катетами.
Каждый катет всегда меньше гипотенузы и при этом сумма катетов всегда больше гипотенузы. Это следует из теоремы о неравенстве в треугольнике.
Свойства
Свойства не имеют нумерации. Нельзя сказать, что катет меньше гипотенузы по свойству 1 или 2. Говорят просто, что катет меньше гипотенузы по свойству прямоугольного треугольника.
Перечислим и докажем свойства прямоугольного треугольника:
- Квадрат гипотенузы равен сумме квадратов катетов. Это не совсем свойство, это теорема Пифагора, но некоторые учебники геометрии упорно продолжают называть его свойством. С другой стороны теорема работает только для прямоугольных треугольников, поэтому в какой-то мере можно считать её свойством. Но в решении всегда пишут «по теореме Пифагора»
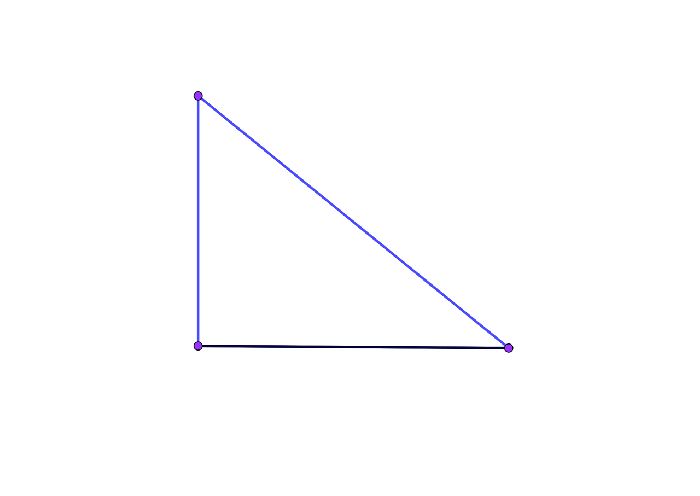
Рис. 1. Прямоугольный треугольник.
- Окружность, описанная вокруг прямоугольного треугольника, имеет центр в середине гипотенузы. Это свойство доказать очень просто. Центр описанной окружности – это точка пересечения серединных перпендикуляров. Серединные перпендикуляры от катетов всегда будут пересекаться в середине гипотенузы. Потому отрезок, который выходит из середины катета, параллельно другому катету – это средняя линия, соединяющая катет и гипотенузу. Вот и все доказательство.
- В прямоугольном треугольнике, медиана, проведенная к гипотенузе, равняется половине гипотенузы.
Докажем это свойство. В прямоугольном треугольнике АВС проведем медиану ВР. Проведем прямую ВМ, проходящую через точку Р так, что ВР=РМ. Тогда два треугольника: АМР и ВРС – будут равны по двум сторонам и углу между ними. АР=РС – потому что Р – это конец медианы, а медиана соединяет вершину и середину противолежащей стороны. То есть, Р – это середина АС. ВР = РМ по построению, а угол АРМ равен углу ВРС как вертикальные углы. Раз треугольники равны, значит, равны и соответственные элементы и ВР=АР, а значит ВР=АР=РС.
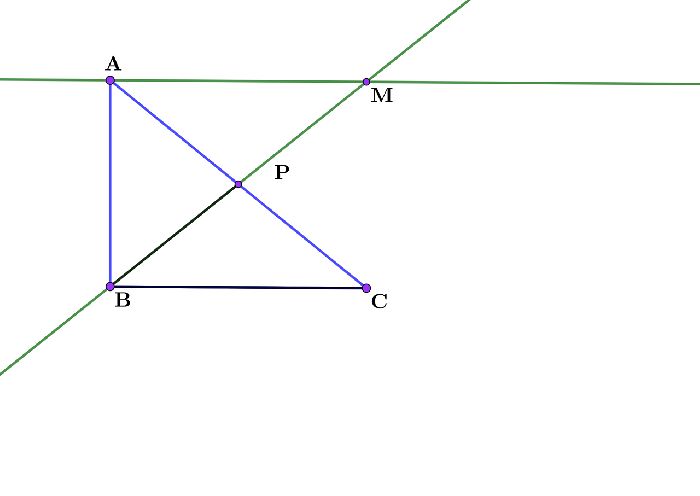
Рис. 2. Рисунок к задаче.
- В прямоугольном треугольнике сумма острых углов равна 90 градусов. В любом треугольнике сумма углов равна 180 градусам. В прямоугольном треугольнике один из углов всегда известен – прямой. Значит можно привести следующую формулу для доказательства этого свойства прямоугольного треугольника: 180-90=90.
Из этого утверждения так же вытекает факт того, что существование тупоугольного прямоугольного треугольника невозможно.
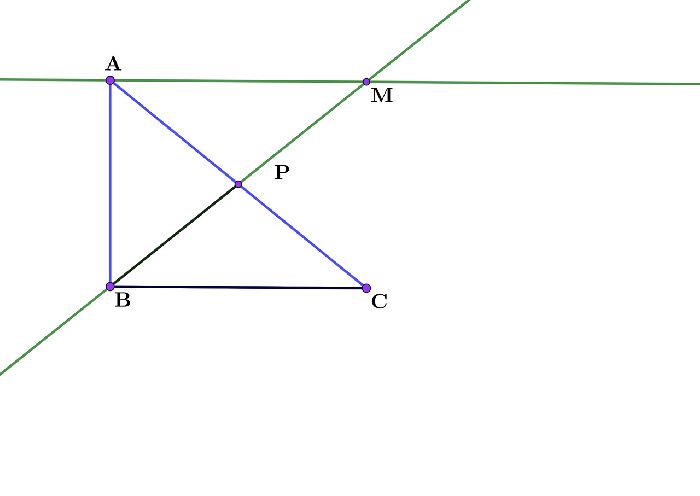
Рис. 3. Сумма углов треугольника.
Что мы узнали?
Из статьи мы узнали об основных свойствах прямоугольного треугольника, применяемых в решении задач, и привели доказательства каждому из них. Мы узнали о том, что тупоугольного прямоугольного треугольника не существует и доказали это при помощи формулы.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-

Константин Никитич
10/10
Оценка статьи
Средняя оценка: 4.4. Всего получено оценок: 160.
Источник
Треугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.
Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой. Гипотенуза является самой большой стороной этого треугольника.
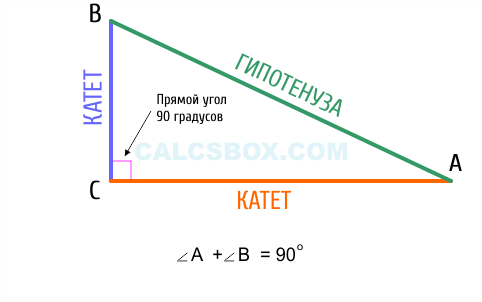
- По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
- Сумма двух острых углов прямоугольного треугольника равна прямому углу.
- Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
- Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Свойства и особенности прямоугольных треугольников
I – е свойство. В прямоугольном треугольнике сумма его острых углов равна 90°. Против большей стороны треугольника лежит больший угол, а против большего угла лежит большая сторона. В прямоугольном треугольнике наибольшим углом, является прямоугольный угол. Если же в треугольнике самый большой угол имеет более 90°, то такой треугольник перестает быть прямоугольным, так как сумма всех углов превысить 180 градусов. Со всего этого следует, что гипотенуза является наибольшей стороной треугольника.
II – е свойство. Катет прямоугольного треугольника, который лежит против угла в 30 градусов, равен половине гипотенузе.
III – е свойство. Если же в прямоугольном треугольнике катет равняется половине гипотенузы, то и угол, который лежит напротив данного катета будет равен 30 градусам.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб — это параллелограмм, у которого все стороны равны.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Азбука Морзе – перечень сигналов из точек и тире, воспроизводящихся с помощью радиосигналов или прерыванием постоянного электрического тока.
1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.
Гектар — это площадь квадрата со стороной 100 м. Ар – площади квадрата со стороной в 10 м. 1 сотка это 100 квадратных метров
Американский нефтяной баррель равен 42 галлонам в английской системе мер или 158,988 л в метрической системе.
1 ом представляет собой электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила.
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Источник
Свойства прямоугольного треугольника
Дорогие семиклассники, вы уже знаете какие геометрические фигуры называются треугольниками, умеете доказывать признаки их равенства. Знаете вы и о частных случаях треугольников: равнобедренных и прямоугольных. Свойства равнобедренных треугольников вам хорошо известны.
Но и у прямоугольных треугольников есть немало свойств. Одно, очевидное, связано с теоремой о сумме внутренних углов треугольника: в прямоугольном треугольнике сумма острых углов равно 90°. Самое удивительное свойство прямоугольного треугольника вы узнаете в 8 классе, когда изучите знаменитую теорему Пифагора.
А сейчас мы поговорим еще о двух важных свойствах. Одно из них относится к прямоугольным треугольникам с углом 30°, а другое к произвольным прямоугольным треугольникам. Сформулируем и докажем эти свойства.
Вам хорошо известно, что в геометрии принято формулировать утверждения обратные к доказанным, когда условие и заключение в утверждении меняются местами. Далеко не всегда обратные утверждения оказываются верными. В нашем случае оба обратных утверждения верны.
Свойство 1.1 В прямоугольном треугольнике катет, лежащий против угла в 30° равен половине гипотенузы.
Доказательство: Рассмотрим прямоугольный ∆ АВС, в котором ÐА=90°, ÐВ=30°, тогда ÐС=60°. Докажем, что . Приложим к ∆ АВС равный ему ∆ АВD. Получим ∆ DBC, в котором ÐС=ÐD=60°, поэтому BD=BC=CD,
, следовательно , что и требовалось доказать.
Свойство 1.2 (обратное к свойству 1.1) Если в прямоугольном треугольнике катет равен половине гипотенузы, то противолежащий ему угол равен 30°.
Док-во: Пусть в ∆ABC ÐA=900 и AC=1/2BC
Продолжим AC за точку А так, что AD=AC. Тогда ∆ABC=∆ABD(по 2-м катетам). BD=BC=2AC=CD, таким образом ∆DBC-равносторонний, ÐС=60о и ÐАВС=30о.
Свойство 2.1 В прямоугольном треугольнике медиана, проведенная к гипотенузе равна половине гипотенузы.
Рассмотрим прямоугольный ∆ АВС, в котором ÐВ=90°.
BD-медиана, то есть AD=DC. Докажем, что .
Для доказательства сделаем дополнительное построение: продолжим BD за точку D так, чтоBD=DN и соединим N с A и C. ∆ADB=∆CDN (BD=DN, AD=DC,ÐADB=ÐCDN как вертикальные).Следовательно: AB=CN и ÐABD=ÐDCN, из равенства этих углов следует параллельность AB и CN, но тогда ÐBCN=90o ∆ABC=∆BCN (по 2 катетам). Но тогда AC=BN и BD=1/2 BN=1/2 AC, что и требовалось доказать.
Свойство 2.2 (обратное к свойству 2.1) Если в треугольнике медиана равна половине стороны к которой она проведена, такой треугольник будет прямоугольным.
Попробуйте доказать это утверждение самостоятельно воспользовавшись свойством равнобедренного треугольника и теоремой о сумме углов треугольника.
Рассмотрим решение некоторых задач
Задача 1
Дано: ∆ABC, ÐC=90o, ÐA=30o, ÐBEC=60o, EC=7см
Найти: AE
Решение:
1. ÐEBC=30o, т. к. в прямоугольном ∆BCE сумма острых углов 90о
2. BE=14см(свойство 1)
3. ÐABE=30o, так как ÐA+ÐABE=ÐBEC (свойство внешнего угла треугольника) поэтому ∆AEB- равнобедренный AE=EB=14см.
Задача 2
AN=10см
Найти: катет AC.
Решение:
1.
ÐBAN/ÐNAC=1/2, а сумма этих углов 90о. Поэтому ÐBAN=30o, ÐNAC=60o.
2. ∆ABN- равнобедренный, AN=BN(свойство 2).
Следовательно ÐВ=30°.
3. (свойство 1).
BC=2AN=20 см (свойство 2).
АС=10 см.
Задача 3. Доказать, что высота и медиана прямоугольного треугольника, проведенные к гипотенузе, образуют угол, равный разности острых углов треугольника.
Дано: ∆ АВС, ÐВАС=90°, АМ-медиана, АН-высота.
Доказать: ÐМАН=ÐС-ÐВ.
Доказательство:
1)ÐМАС=ÐС (по свойству 2 ∆ АМС-равнобедренный, АМ=СМ)
2)ÐМАН=ÐМАС-ÐНАС=ÐС-ÐНАС.
Остается доказать, что ÐНАС=ÐВ. Это следует из того, что ÐВ+ÐС=90°(в ∆ АВС) и ÐНАС+ÐС=90° (из ∆ АНС).
Итак, ÐМАН=ÐС-ÐВ, что и требовалось доказать.
Задача 4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найти острые углы треугольника.
Дано: ∆АВС, ÐВАС=90°, АН-высота, .
Найти: ÐВ, ÐС.
Решение: Проведем медиану АМ. Пусть АН=х, тогда ВС=4х и
ВМ=МС=АМ=2х.
В прямоугольном ∆ АМН, гипотенуза АМ в 2 раза больше катета АН, поэтому ÐАМН=30°. Так как ВМ=АМ,
ÐВ=ÐВАМ=15°. Но тогда ÐС=90°-15°=75°.
При решении этой задачи мы применили не только свойство 1, но и утверждение обратное этому свойству. Сформулируем и докажем это утверждение. Итак, если в прямоугольном треугольнике катет равен половине гипотенузы, то противолежащий ему угол равен 30°.
Док-во: Пусть в ∆ABC ÐA=900 и AC=1/2BC
Продолжим AC за точку А так, что AD=AC. Тогда ∆ABC=∆ABD(по 2-м катетам). BD=BC=2AC=CD, таким образом ∆DBC-равносторонний, ÐС=60о и ÐАВС=30о.
Задача 5
В равнобедренном треугольнике один из углов 120о, основание равно 10 см. Найти высоту, проведенную к боковой стороне.
Решение : для начала отметим, что угол 120о может быть только при вершине треугольника и что высота проведенная к боковой стороне попадет на её продолжение.
Итак, АВ=ВС, ÐАВС=120о, АН-высота, АС=10см.
Нетрудно видеть, что ÐС=30о, поэтому АН=1/2АС=5см
(свойство 1).
Задача 6
К вертикальной стене прислонили лестницу. На середине лестницы сидит котенок. Вдруг лестница начала скользить вниз по стене. Какую траекторию будет описывать котенок?
АВ – лестница, К – котенок.
При любом положении лестницы, пока она окончательно не упала на землю ∆АВС- прямоугольный. СК – медиана ∆АВС.
По свойству 2 СК=1/2АВ. То есть в любой момент времени длина отрезка СК постоянна.
Ответ: точка К будет двигаться по дуге окружности с центром С и радиусом СК=1/2АВ.
Задачи для самостоятельного решения.
Один из углов прямоугольного треугольника равен 60о, а разность гипотенузы и меньшего катета равна 4см. найти длину гипотенузы. В прямоугольном ∆ АВС с гипотенузой ВС и углом В, равным 60о, проведена высота АD. Найти DC, если DB=2см. В ∆АВС ÐС=90о, СD – высот, ВС=2ВD. Докажите, что АD=3ВD. Высота прямоугольного треугольника делит гипотенузу на части 3см и 9см. Найти углы треугольника и расстояние от середины гипотенузы до большего катета. Биссектриса разбивает треугольник на два равнобедренных треугольника. Найти углы исходного треугольника. Медиана разбивает треугольник на два равнобедренных. Можно ли найти углы
Исходного треугольника?
Источник
