Какие свойства используют при решении уравнений
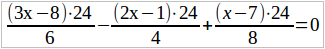
Муниципальное бюджетное общеобразовательное учреждение «Школа № 12 г.Феодосии Республики Крым»
Урок математики в 6 классе
Тема урока:
Учитель математики Дубинина Татьяна Яковлевна
2016г.
Цель урока: раскрыть понятие уравнения, решения уравнения; рассмотреть основные свойства уравнений; разобрать понятие линейного уравнения с одной переменной; закрепить на простейших примерах. Продолжать формировать умения и навыки выполнения действий над рациональными числами.
Ход урока
Организационный момент (слайд 2): на тему выделено 12 часов, планируются 1 самостоятельная работа, 1 математический диктант и 1 контрольная работа.
Оглашение цели урока: сегодня наша с вами задача понять, что же такое уравнение, его корни, что значит решить уравнение, разобрать свойства уравнений и к концу урока на начальном уровне уже уметь ими пользоваться.
Восприятие новой темы
1.Давайте подумаем и попробуем сами определить: что же такое уравнение. Приведите пример уравнения и попробуйте дать определение уравнению. Подумайте, что должно быть в записи, чтобы это было уравнение.
(Дети пытаются приводить примеры, учитель записывает их на доске)
Слайд 3
1)2х +6;
2)4+9=13;
3)х+5=8.
Обсудить каждую запись:
1)буквенное выражение
Вопрос классу: чего не хватает в этой записи? Ответ: знака «равно» и ответа;
2)числовое равенство
Вопрос классу: почему это не уравнение? Ответ: нет буквы (переменной)
3)уравнение
Итак, давайте попробуем дать определение уравнения с одной переменной: (под запись в конспекты) Уравнением с одной переменной называется равенство, содержащее одну переменную.
Предложить нескольким учащимся повторить определение уравнения и ответить на вопрос, какие из записей на слайде являются уравнением:
Слайд 4
х+5;
х2+х=3;
х-у=1;
2х+1=х-5;
8+3=2+9.
2.Теперь разберём, что же называется корнем уравнения с одной переменной.
Слайд 5
х+2=5
Из чисел -1; 4; 3; 0 выберите корень данного уравнения.
1)х=-1
-1+2=1, 15, значит, х=-1 не является корнем уравнения
2)х=4
4+2=6, 65, значит, х=4 не является корнем уравнения
3)х=3
3+2=5, 5=5, значит, х=3 является корнем уравнения
4)х=0
0+2=2, 25, значит, х=0 не является корнем уравнения
Делаем вывод: (под запись в тетрадь)
Корнем уравнения с одной переменной называется числовое значение переменной, обращающее уравнение в верное числовое равенство.
4. Давайте решим следующие уравнения:
Слайд 6
х2=4; 0х=6; 0х=0; х+2=-9
Записывают уравнения в тетрадь и решают их, обсуждая:
1)х2=4;
х=2 или х=-2;
2)0х=6;
нет корней;
3)0х=0;
х-любое число.
Делаем вывод (с записью в тетради):
Решить уравнение – это значит найти все его корни или показать, что таковых нет.
5.Разберём теперь свойства уравнений (слайд 6). Все видели чашечные весы на рынке, представим себе, что на одну чашу положили 5 кг сахара, а на вторую – 5-ти килограммовую гирю. Что при этом происходит с весами?
Ответ: весы находятся в равновесии.
Вопрос: если теперь на обе чаши добавить по 1 кг, что при этом изменится, а что – нет?
Ответ: изменится вес на каждой чаше, но не изменится равновесие.
Вот так и в уравнении: важно равновесие, мы сейчас выясним, что можно делать с уравнением, чтобы корни его не изменились.
Вывод:
свойство 1
Корень уравнения не изменится, если к обеим частям прибавить одно и то же выражение.
Пример
2х+3=-х+6; /-3
2х+3-3=-х+6-3;
2х=-х+6-3; /+х
2х+х=-х+6-3+х;
2х+х=6-3;
3х=3;
х=1.
Из этого примера сделать вывод:
Свойство 2
Корень уравнения не изменится, если перенести слагаемое из одной его части в другую, поменяв при этом знак слагаемого на противоположный.
Пример:
3х-8=2х+6;
3х-2х=6+8;
х=14.
Свойство 3
Корень уравнения не изменится, если обе его части умножить или разделить на одно и то же число, отличное от нуля.
Пример:
4-8х=х-5;
-8х-х=-5-4; /*(-1)
8х+х=5+4;
9х=9;
х=1.
Свойство 4
Корень уравнения не изменится, если раскрыть скобки, привести подобные слагаемые, упростить обе части уравнения.
Пример:
5х-8(2-х)=11+6(х-1);
5х-16+8х=11+6х-6;
13х-16=5+6х;
13х-6х=5+16;
7х=21;
х=3.
4.Осмысление
Решают сначала самостоятельно, чтобы понять – насколько хорошо усвоили тему, а затем у доски проверяем.
618(а, б) Является ли число 2 корнем уравнения:
а) х-2=0; б)х+4=0.
626(а) Решить уравнение 3х+2х=10
627(а) Решить уравнение х+3=3х-7
628(а) Решить уравнение 2(х-5)=9
Задать домашнее задание: п.3.9 – учить определение уравнения, знать понятие корня уравнения и знать, что значит решить уравнение, решать №№618(в, д), 626(г, ж), 627(г). Подумайте дома и попробуйте ответить на вопрос: зачем нужны уравнения?
Рефлексия:
1)что же мы сегодня изучали на уроке?
2)достигли ли мы поставленной цели?
3)всё ли было понятно или на что-то необходимо обратить внимание на следующем уроке?
Источник
50. Свойства равенств, на которых основывается решение уравнений. Возьмем какое-нибудь уравнение, не очень сложное, например:
7x – 24 = 15 – 3x
или
x/2 – (x – 3)/3 – (x – 5)/6 = 1
Мы видим в каждом уравнении знак равенства: все то, что написано слева от знака равенства, называется левою или первою частью уравнения (в первом уравнении 7x – 24 является левою или первою частью, а во втором x/2 – (x – 3)/3 – (x – 5)/6 есть первая, или левая, часть); все то, что написано справа от знака равенства, называется правою или второю частью уравнения (15 – 3x есть правая часть первого уравнения, 1 является правою, или вторю, частью 2-го уравнения).
Каждая часть любого уравнения выражает собою некоторое число. Числа, выражаемые левою и правою частью уравнения, должны быть равны между собою. Нам ясно: если мы к каждому из этих чисел прибавим по одинаковому числу, либо вычтем из них по одинаковому числу, либо каждое из них умножим на одинаковое число, либо, наконец, разделим на одно и то же число, то результаты этих действий должны также быть равными между собою. Другими словами: если a = b, то a + c = b + c, a – c = b – c, ac = bc и a/c = b/c. По поводу деления следует, однако, иметь в виду, что в арифметике не имеется деления на нуль — мы не умеем, например, число 5 разделить на нуль. Поэтому в равенстве a/c = b/c число c не может быть равным нулю.
Итак:
- К обеим частям уравнения можно прибавить или из них вычесть по одинаковому числу.
- Обе части уравнения можно умножить или разделить на одно и то же число, исключая случай, когда это число может оказаться равным нулю.
Пользуясь этими свойствами уравнения, мы можем найти удобный способ решать уравнения. Выясним этот случай на примерах.
Пример 1. Пусть надо решить уравнение
5x – 7 = 4x + 15.
Мы видим, что первая часть уравнения содержит два члена; один из них 5x, содержащий неизвестный множитель x, можно назвать неизвестным членом, а другой –7 – известным. Во второй части уравнения также 2 члена: неизвестный 4x и известный +15. Сделаем так, чтобы в левой части уравнения оказались только неизвестные члены (а известный член –7 уничтожился бы), а в правой части оказались бы только известные члены (а неизвестный член +4x уничтожился бы). Для этой цели прибавим к обеим частям уравнения одинаковые числа: 1) прибавим по +7 (чтобы уничтожился член –7) и 2) прибавим по –4x (чтобы уничтожился член +4x). Тогда получим:
5x – 7 + 7 – 4x = 4x + 15 + 7 – 4x
Сделав в каждой части уравнения приведение подобных членов, получим
x = 22.
Это равенство и является решением уравнения, так как оно указывает, что для x надо взять число 22.
Пример 2. Решить уравнение:
8x + 11 = 7 – 4x
Опять прибавим к обеим частям уравнения по –11 и по +4x, получим:
8x + 11 – 11 + 4x = 7 – 4x – 11 + 4x
Выполнив приведение подобных членов, получим:
12x = –4
Разделим теперь обе части уравнения на +12, получим:
x = –4/12 или x = –1/3
(первую часть уравнения 12x разделить на 12 – получим 12x/12 или просто x; вторую часть уравнения –4 разделить на +12 – получим –4/12 или –1/3).
Последнее равенство и является решением уравнения, так как оно указывает, что для x надо взять число –1/3.
Пример 3. Решить уравнением
x – 23 = 3 · (2x – 3)
Раскроем сначала скобки, получим:
x – 23 = 6x – 9
Прибавим к обеим частям уравнения по +23 и по –6x, – получим:
x – 23 + 23 – 6x = 6x – 9 + 23 – 6x.
Теперь, для того, чтобы впоследствии ускорить процесс решения уравнения, не будем сразу выполнять приведение всех подобных членов, а только заметим, что члены –23 и +23 в левой части уравнения взаимно уничтожаются, также члены +6x и –6x в первой части взаимно уничтожаются – получим:
x – 6x = –9 + 23.
Сравним это уравнение с начальным: вначале было уравнение:
x – 23 = 6x – 9
Теперь получили уравнение:
x – 6x = –9 + 23.
Мы видим, что в конце концов оказалось, что член –23, находившийся сначала в левой части уравнения, теперь как бы перешел в правую часть уравнения, причем у него переменился знак (в левой части начального уравнения был член –23, теперь его там нет, но зато в правой части уравнения имеется член + 23, которого там раньше не было). Так же точно в правой части уравнения был член +6x, теперь его там нет, но появился зато в левой части уравнения член –6x, которого раньше там не было. Рассматривая с этой точки зрения примеры 1 и 2, мы придем к общему заключению:
Можно любой член уравнения перенести из одной части в другую, меняя знак у этого члена (в дальнейших примерах мы будем этим пользоваться).
Итак, возвращаясь к нашему примеру, мы получили уравнение
x – 6x = –9 + 23
Выполним приведение подобных членов:
–5x = +14
Разделим обе части уравнения на –5. Тогда получим:
x = –2(4/5)
[–5x : (–5) получим x] – это и есть решение нашего уравнения.
Пример 4. Решить уравнение:
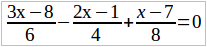
Сделаем так, чтобы в уравнении не было дробей. Для этой цели найдем общего знаменателя для наших дробей – общим знаменателем служит число 24 – и умножим на него обе части нашего уравнения (можно, ведь, чтобы равенство не нарушалось, умножить на одно и то же число только обе части уравнения). В первой части 3 члена, причем каждый член является дробью — надо, следовательно, каждую дробь умножить на 24: вторая часть уравнения есть 0, а нуль умножить на 24 — получим нуль. Итак,
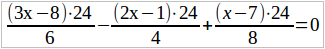
Мы видим, что каждая из наших трех дробей, благодаря тому, что она умножена на общее наименьшее кратное знаменателей этих дробей, сократится и сделается целым выражением, а именно получим:
(3x – 8) · 4 – (2x – 1) · 6 + (x – 7) · 3 = 0
Конечно, желательно все это выполнить в уме: надо вообразить, что, например, числитель первой дроби заключается в скобки и умножается на 24, после чего воображение поможет нам увидеть сокращение это дроби (на 6) и конечный результат, т. е. (3x – 8) · 4. Тоже имеет место и для остальных дробей. Раскроем теперь в полученном уравнении (в его левой части) скобки:
12x – 32 – 12x + 6 + 3x – 21 = 0
(обратим внимание, что здесь понадобилось двучлен 2x – 1 умножить на 6 и полученное произведение 12x – 6 вычесть из предыдущего, благодаря чему знаки членов этого произведения должны перемениться — выше и написано –12x + 6). Перенесем известные члены (т. е. –32, +6 и –21) из левой части уравнения в его правую часть, причем (как мы уже знаем) знаки этих членов должны перемениться — получим:
12x – 12x + 3x = 32 – 6 + 21.
Выполним приведение подобных членов:
3x = 47
(при навыке должно сразу выполняться и перенесение нужных членов из одной части уравнения в другую и приведение подобных членов), разделим, наконец, обе части уравнения на 3 — получим:
x = 15(2/3) — это и есть решение уравнения.
Пример 5. Решить уравнение:
5 – (3x + 1)/7 = x + (2x – 3)/5
Здесь две дроби, и их общий знаменатель равен 35. Умножим, чтобы освободить уравнение от дробей, обе части уравнения на общего знаменателя 35. В каждой части нашего уравнения 2 члена. При умножении каждой части на 35 должно каждый член умножить на 35 — получим:
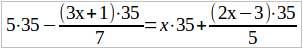
Дроби сократятся — получим:
175 – (3x + 1) · 5 = 35x + (2x – 3) · 7
(конечно, можно было бы при навыке написать сразу это уравнение).
Выполним все действия:
175 – 15x – 5 = 35x + 14x – 21.
Перенесем все неизвестные члены из правой части (т. е. члены +35x и +14x) в левую, а все известные члены из левой части (т. е. члены +175 и –5) в правую — следует при этом не забывать у переносимых членов менять знак:
–15x – 35x – 14x = –21 – 175 + 5
(член –15x, как раньше был в левой части, так и теперь в ней остался — у него поэтому отнюдь не следует менять знака; аналогичное имеет место и для члена –21). Сделав приведение подобных членов, получим:
–64x = –191.
[Возможно сделать так, чтобы не было знака минус в обеих частях уравнения; для этого умножим обе части уравнения на (–1), получим 64x = 191, но этого можно и не делать.]
Разделим затем обе части уравнения на (–64), получим решение нашего уравнения
x = 2(63/64)
[Если умножили обе части уравнения на (–1) и получили уравнение 64x = 191, то теперь надо обе части уравнения разделить на 64.]
На основании того, что пришлось выполнять в примерах 4 и 5, мы можем установить: можно освободить уравнение от дробей — для этого надо найти общего знаменателя для всех дробей, входящих в уравнение (или наименьшее общее кратное знаменателей всех дробей) и на него умножить обе части уравнения — тогда дроби должны исчезнуть.
Пример 6. Решить уравнение:
5x = 4x.
Перенеся член 4x из правой части уравнения в левую, получим:
5x – 4x = 0 или x = 0.
Итак, решение найдено: для x надо взять число нуль. Если мы заменим в данном уравнении x нулем, получим 5 · 0 = 4 · 0 или 0 = 0, что указывает на выполнение требования, выражаемого данным уравнением: найти такое число для x, чтобы одночлен 5x оказался равен тому же самому числу, как и одночлен 4x.
Если кто-либо подметит с самого начала, что обе части уравнения 5x = 4x можно разделить на x и выполнит это деление, то получится явная несообразность 5 = 4! Причиною этого является то обстоятельство, что деление 5x/x в данном случае выполнить нельзя, так как, мы видели выше, вопрос, выражаемый нашим уравнением, требует, чтобы x = 0, а деление на нуль не выполнимо.
Заметим еще, что и умножение на нуль требует некоторой внимательности: умножая на нуль и два неравных числа, мы получим в результате этих умножений равные произведения, а именно — нули.
Если, например, мы имеем уравнение
x – 3 = 7 – x (его решение: x = 5)
и если кто-либо захочет к нему применить свойство «обе части уравнения можно умножить на одно и тоже число» и умножить обе части на x, то получит:
x2 – 3x = 7x – x2.
После этого может обратить на себя внимание, что все члены уравнения содержат множителя x, из чего можно сделать заключение, что для решения этого уравнения можно взять число нуль, т. е. положить x = 0. И в самом деле, тогда получим:
02 – 3 · 0 = 7 · 0 – 02 или 0 = 0.
Однако, это решение x = 0, очевидно, не годится для данного уравнения x – 3 = 7 – x; заменяя в нем x нулем, получим явную несообразность: 3 = 7!
Источник
Первое печатное появление знака равенства в книге Роберта Рекорда в 1557 году (записано уравнение 14x + 15 = 71)
Уравне́ние — равенство вида
,
где чаще всего в качестве выступают числовые функции, хотя на практике встречаются и более сложные случаи — например, уравнения для вектор-функций, функциональные уравнения и другие.
Решение уравнения[править | править код]
Иллюстрация графического метода нахождения корней уравнения x = f(x)
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).
Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными».
Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.
Про корни говорят, что они удовлетворяют данному уравнению.
Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.
Равносильные уравнения[править | править код]
Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней.
Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.
Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения.
Третье важное свойство задаётся теоремой: если функции заданы над областью целостности, то уравнение
эквивалентно совокупности уравнений
.
Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений, и позволяет находить корни первого уравнения в два приёма, решая каждый раз более простые уравнения.
Основные свойства[править | править код]
С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:
- в любой части уравнения можно раскрыть скобки;
- в любой части уравнения можно привести подобные слагаемые;
- любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный;
- к обеим частям уравнения можно прибавить одно и то же выражение;
- из обеих частей уравнения можно вычесть одно и то же выражение;
- обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.
Уравнения, которые являются результатом этих операций, являются эквивалентными начальному уравнению. Однако для свойств 4 и 5 существует ограничение: в случае прибавления к обеим частям уравнения одного и того же выражения (или в случае вычитания из обеих частей уравнения одного и того же выражения), содержащего неизвестное и теряющего смысл при неизвестном, принимающем значения корней данного уравнения, получится уравнение, неэквивалентное исходному (начальному). Но если к обеим частям уравнения прибавить одно и то же выражение (или из обеих частей уравнения вычесть одно и то же выражение), содержащее неизвестное и теряющее смысл лишь при значениях неизвестного, не являющихся корнями данного уравнения, то получится уравнение, эквивалентное начальному.
Умножение или деление обеих частей уравнения на выражение, содержащее неизвестное, может привести, соответственно, к появлению посторонних корней или к потере корней.
Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.
Следствие уравнения и посторонние корни[править | править код]
Уравнение
называется следствием уравнения
,
если все корни второго уравнения являются корнями первого. Первое уравнение может иметь дополнительные корни, которые для второго уравнения называются посторонними. Посторонние корни могут появиться при преобразованиях, необходимых для нахождения корней уравнений. Для того чтобы их обнаружить, необходимо проверить корень подстановкой в исходное уравнение. Если при подстановке уравнение становится тождеством, то корень настоящий, если нет — посторонний.
Пример[править | править код]
Уравнение при возведении обеих частей в квадрат даёт уравнение , или . Оба уравнения являются следствием исходного. Последнее из них легко решить; оно имеет два корня и .
При подстановке первого корня в исходное уравнение образуется тождество . При подстановке другого корня получается неправильное утверждение . Таким образом, второй корень нужно отбросить как посторонний.
Виды уравнений[править | править код]
Различают алгебраические уравнения, уравнения с параметрами, трансцендентные, функциональные, дифференциальные и другие виды уравнений.
Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ существования и количества корней в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.
К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения не выше четвёртой степени: линейное, квадратное, кубическое уравнения и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.
Уравнения, в которые входят трансцендентные функции, называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.
В общем случае, когда аналитического решения найти не удаётся, применяют вычислительные (численные) методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения.
Алгебраические уравнения[править | править код]
Алгебраическим уравнением называется уравнение вида
где — многочлен от переменных , которые называются неизвестными.
Коэффициенты многочлена обычно берутся из некоторого поля , и тогда уравнение называется алгебраическим уравнением над полем . Степенью алгебраического уравнения называют степень многочлена .
Например, уравнение
является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.
Линейные уравнения[править | править код]
Квадратные уравнения[править | править код]
где — свободная переменная, , , — коэффициенты, причём .
Выражение называют квадратным трёхчленом. Корень такого уравнения (корень квадратного трёхчлена) — это значение переменной , обращающее квадратный трёхчлен в нуль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент называют первым или старшим, коэффициент называют вторым или коэффициентом при , называется свободным членом этого уравнения. Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент : , где , а . Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля. Неполным квадратным уравнением называется такое, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.
Для нахождения корней квадратного уравнения в общем случае следует пользоваться приводимым ниже алгоритмом:
Графиком квадратичной функции в прямоугольных координатах является парабола. Она пересекает ось абсцисс в точках, соответствующих корням квадратного уравнения .
Кубические уравнения[править | править код]
График кубической функции
Для графического анализа кубического уравнения в прямоугольных координатах используется кубическая парабола.
Любое кубическое уравнение канонического вида можно привести к более простому виду
,
поделив его на и подставив в него замену . При этом коэффициенты будут равны:
,
.
Уравнение четвёртой степени[править | править код]
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).
Так как является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если , то функция возрастает до плюс бесконечности с обеих сторон, и следовательно, имеет глобальный минимум. Аналогично, если , то функция убывает до минус бесконечности с обеих сторон, и следовательно, имеет глобальный максимум.
Иррациональные и рациональные уравнения[править | править код]
- Рациональное уравнение – это такой вид уравнения в которой левая и правая части рациональные выражения. В записи уравнения имеются только сложение, вычитание, умножение , деление , а также возведение в степень целого числа.
- Иррациональное уравнение — это уравнение, содержащее неизвестное под знаком корня. или возведённое в степень, которую нельзя свести к целому числу.
Системы линейных алгебраических уравнений[править | править код]
Система уравнений вида:
| (1) |
Здесь — количество уравнений, а — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной. Система называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).
Совместная система называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Уравнения с параметрами[править | править код]
Уравнением с параметрами называется математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров. Решить уравнение с параметром означает:
- Найти все системы значений параметров, при которых данное уравнение имеет решение.
- Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Уравнения с параметром могут быть как линейными, так и нелинейными.
Пример линейного уравнения с параметром:
Пример нелинейного уравнения с параметром:
где — независимая переменная, — параметр.
Трансцендентные уравнения[править | править код]
Трансцендентным уравнением называется уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например:
Более строгое определение таково: трансцендентное уравнение — это уравнение вида , где функции и являются аналитическими функциями, и по крайней мере одна из них не является алгебраической.
Функциональные уравнения[править | править код]
Функциональным уравнением называется уравнение, выражающее связь между значением функции (или функций) в одной точке с её значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин «функциональное уравнение» обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Например:
- функциональному уравнению
где — гамма-функция Эйлера, удовлетворяет дзета-функция Римана ζ.
- Следующим трём уравнениям удовлетворяет гамма-функция; она является единственным решением этой системы трёх уравнений:
(формула дополнения Эйлера).
- Функциональное уравнение
где , , , являются целыми числами, удовлетворяющими равенству , то есть , определяет как модулярную форму порядка k.
Дифференциальные уравнения[править | править код]
Дифференциальным уравнением называется уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные. Порядок дифференциального уравнения — наибольший порядок производных, входящих в него. Решением дифференциального уравнения порядка n называется функция , имеющая на некотором интервале (a, b) производные до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.
Все дифференциальные уравнения можно разделить на
- обыкновенные дифференциальные уравнения (ОДУ), в которые входят только функции (и их производные) от одного аргумента:
или ,
где — неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной ; штрих означает дифференцирование по .
- и дифференциальные уравнения в частных производных, в которых входящие функции зависят от многих переменных:
,
где — независимые переменные, а — функция этих переменных.
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
Примеры уравнений[править | править код]
См. также[править | править код]
- Диофантово уравнение
- Линейное уравнение
- Квадратное уравнение
- Решение какого-либо уравнения построением
- Система уравнений
- Переменная
Примечания[править | править код]
- ↑ Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004. — 280 с.
Литература[править | править код]
- Бекаревич А. Б. Уравнения в школьном курсе математики. — Минск: Нар. асвета, 1968. — 152 с.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: Изд. АСТ, 2003, ISBN 5-17-009554-6.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Маркушевич, Л. А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы / Л. А. Маркушевич, Р. С. Черкасов. / Математика в школе. — 2004. — № 1.
Ссылки[править | править код]
- Уравнение — статья из Большой советской энциклопедии.
- Уравнения // Энциклопедия Кольера. — Открытое общество. 2000.
- Уравнение // Энциклопедия Кругосвет
- Уравнение // Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- EqWorld — Мир математических уравнений — содержит обширную информацию о математических уравнениях и системах уравнений.
Источник
