Какие свойства используют в пропорции
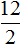
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 марта 2020; проверки требует 1 правка.
У этого термина существуют и другие значения, см. Пропорция.
Пропо́рция (лат. proportio «соразмерность, выравненность частей; определённое соотношение частей между собой») — равенство отношений двух [и более] пар чисел и , т. е. равенство вида , или, в других обозначениях, равенство
(часто читается как: « относится к так же, как относится к »). В этом случае и называют крайними, и — средними членами пропорции. Такую пропорцию ещё называют геометрической, чтобы не путать с арифметической и гармонической пропорциями.
Основные свойства пропорций[править | править код]
(перестановка средних членов пропорции),
(перестановка крайних членов пропорции).
- Увеличение и уменьшение пропорции. Если , то
(увеличение пропорции),
(уменьшение пропорции).
- Составление пропорции сложением и вычитанием. Если , то
(составление пропорции сложением),
(составление пропорции вычитанием).
Доказательство (составление пропорции сложением и вычитанием)
Докажем для сложения. Выразим через остальные члены пропорции: . Тогда:
Для вычитания доказательство аналогично. ■
История[править | править код]
Первое известное определение равных пропорций было дано как равенство последовательных вычитаний[1], современным языком это можно выразить как равенство цепных дробей для отношений величин.[2]
Позже Евдокс Книдский упростил определение, равенство пропорций им определялось как одновременное выполнение одной из трёх пар соотношений
для любой пары натуральных чисел и .
Это определение даётся в «Началах» Евклида.
С появлением вещественных чисел отпала необходимость в специальной теории пропорций, древние математики не рассматривали пропорции длины как числа.
Определение Евдокса, данное в несколько более абстрактном виде, использовалось далее при определении вещественных чисел Дедекиндом через сечения.
Связанные определения[править | править код]
Арифметическая пропорция[править | править код]
Равенство двух разностей иногда называют арифметической пропорцией[3].
Гармоническая пропорция[править | править код]
Если у геометрической пропорции средние члены равны, а последний является разницей между первым и средним, такая пропорция называется гармонической: . В этом случае, разложение на сумму двух слагаемых и называется гармоническим делением или золотым сечением[4].
Задачи на тройное правило[править | править код]
В содержание задачи на простое тройное правило входят две величины, связанные пропорциональной зависимостью, при этом даются два значения одной величины и одно из соответствующих значений другой величины, требуется же найти её второе значение.
Задачами на сложное тройное правило называют задачи, в которых по ряду нескольких (более двух) пропорциональных величин требуется найти значение одной из них, соответствующее другому ряду данных значений величин[5][6].
См. также[править | править код]
- Пропорциональность
Примечания[править | править код]
Литература[править | править код]
- Ван дер Варден, Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. / пер. с голл. И. Н. Веселовского. — М.: ГИФМЛ, 1959.
Источник
Здравствуйте, уважаемые читатели! Сегодня хочу с Вами поговорить на такую замечательную тему, как пропорции. Понятия “пропорция, пропорционально” повсеместно используются не только в математике, но и в повседневной жизни. Сначала предлагаю посмотреть на пропорции с математической точки зрения, затем с точки зрения практического применения.
Пропорция
Итак, давайте вспомним, что же такое пропорция? Почему вспомним? – спросите Вы – все и так знают, что это такое. Да, знают и понимают это практически все, но кто сможет сходу дать ей определение? )) В самом широком смысле, пропорция – это равенство соотношений. С точки зрения математики, соотношение может быть арифметическим или геометрическим. Например числа 5, 3 и 6, 4 составляют арифметическую пропорцию, так как разность между 5 и 3 равна разности между 6 и 4. А числа 18, 3 и 24, 4 находятся в пропорции геометрической, потому что отношение 18 к 3 равно отношению 24 к 4. Это как разница между арифметической и геометрической прогрессиями. Есть ещё и пропорция, которая называется гармонической. В отличии от двух предыдущих, в ней участвуют не четыре, а два числа. Но они относятся друг к другу по правилу золотого сечения, о котором я уже писал. Двумя целыми числами, составляющими гармоническую пропорцию, могут быть достаточно большие члены ряда Фибоначчи, например, 987 и 610, так как 987/610=(987+610)/987=1,61803=Ф (с точностью до 5-го знака).
Более пристальное внимание в школьном курсе математики уделяется геометрическим пропорциям, так как у арифметических особых свойств нет, кроме того, что это просто равенство двух разностей. А поскольку о золотом сечении, как говорилось выше, я уже достаточно подробно писал, то далее речь пойдёт о свойствах геометрической пропорции. Дальше для краткости я буду писать просто пропорция, имея ввиду именно геометрическую.
Вспомним, что в пропорции a/b=c/d числа a и d называют крайними членами, b и c – средними членами пропорции. Первое свойство пропорции – это сохранение равенства при перемножении крайних и средних членов:
Свойство пропорции
Второе, на мой взгляд, самое важное, свойство пропорции – это то, что при перемене местами крайних членов, так же как и средних, равенство пропорции сохраняется:
Свойства пропорции
Как видно из этих свойств также следует, что равенство сохраняется и при перемене местами числителей и знаменателей. Честно признаюсь, меня это до сих пор завораживает! ))
Есть также свойство увеличения и уменьшения пропорции:
Свойство пропорции
Но и это ещё не всё! Есть также свойство составления пропорции сложением и вычитанием:
Свойство пропорции
По-моему, это просто поразительно! Четыре числа – и столько равенств!
Теперь о практике. Использование в жизни пропорций настолько велико, что примеры можно перечислять бесконечно. Это, в первую очередь, архитектура; а так же искусство: живопись, скульптура, музыка, и т. д. Применяют пропорции, конечно же, и в самых различных вычислениях. Вспомните мой пример из статьи о подобных треугольниках. Если ещё не читали, обязательно прочитайте. По-моему, свойства пропорций имеют огромное значение в нашей жизни. Часто мы об этом даже не догадываемся ))
Надеюсь, Вам было интересно. Спасибо, что прочитали!
Чтобы не пропустить новых интересных статей о математике, предлагаю Вам подписаться на мой канал.
P.S. Ответ на задачку о гусях из прошлой статьи. Правильное число: 36.
Предыдущая статья
Следующая статья
Источник
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение равно отношению
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение не пропорционально отношению .
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
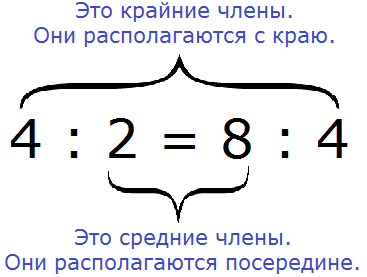
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
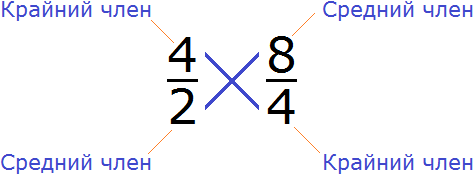
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
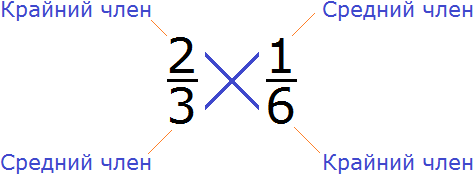
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Источник
Пропорции
Мы достаточно часто в жизни сталкиваемся с понятием «пропорция». Это и пропорция предмета, и пропорция в каком-нибудь кулинарном рецепте, и пропорции в искусстве. Только далеко не все понимают, что это такое. Разберёмся.
Пропорцией называется равенство двух отношений.
То есть, при делении а на b получается такое же число, как и при делении cна d.
Пример 1. Отношение числа 28 к числу 7 равно 4; отношение числа 64 к числу 16 тоже равно 4, значит, является верной пропорцией.
Два числа, которые мы пишем первым и последним, называются крайними членами пропорции; а два числа, которые мы пишем в середине, называются среднимичленами пропорции.
В нашей формуле aиd– крайние члены, а bи c– средние члены.
У пропорции есть замечательное свойство.
Основное свойство пропорции:
Пропорция верна тогда и только тогда, когда произведение её крайних членов равно произведению её средних членов.
Пример 2. Проверить, является ли пропорция верной.
Произведение крайних членов равно:
Произведение средних членов равно:
Эти два произведения равны, значит, данная пропорция верна.
Есть ещё одно свойство пропорции:
Если в верной пропорции поменять местами крайние (или средние) члены, то получившаяся пропорция тоже будет верна.
Пример 3. Пропорция верна. Значит, будут верны и такие пропорции:
Используя основное свойство пропорции, можно задать алгоритм нахождения неизвестного члена пропорции.
Чтобы найти неизвестный крайний член пропорции, нужно перемножить средние члены и разделить на известный крайний член.
Чтобы найти неизвестный средний член пропорции, нужно перемножить крайние члены и разделить на известный средний член.
Пример 4. Найти неизвестный член пропорции:
Ответ: 35
Из чисел 16; 6; 8; 12 составить верную пропорцию.
Из чисел 2,4; 4,2; 7,2; 12,6 составить верную пропорцию.
Из чисел 1,5; 4,9; 2,1; 3,5 составить верную пропорцию.
Из чисел 2,3; 9,3; 3,1; 6,9 составить верную пропорцию.
Верна ли пропорция ?
Верна ли пропорция ?
Верна ли пропорция ?
Верна ли пропорция ?
Решить уравнение:
Масса 15 одинаковых деталей составила 37,5 кг. Какова масса 12 таких деталей?
До обеда скосили 2,8 га, что составляет 24% площади луга. После обеда скосили ещё 2,1 га. Сколько процентов луга скосили за день?
Когда цех выпустил 360 приборов, то он выполнил 120% месячной нормы. Какова месячная норма?
Самолёт пролетел расстояние между двумя аэродромами за 6 ч со скоростью 850 км/ч. За сколько времени пролетит это расстояние другой самолёт, скорость которого на 150 км/ч больше скорости первого?
На 20 км пути автомобиль расходует л горючего. Сколько горючего израсходует этот же автомобиль на 50 км пути?
Для отопления здания заготовлено угля на 180 дней при норме расхода 0,6 т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5 т?
Краеобмёточная машина 0,6 м ткани обработает за 2,16 мин. Сколько потребуется времени, чтобы обметать 1,25 м такой ткани? Сколько метров можно обметать за 1,44 мин?
Распилили 3,2 м3 дров, что составляет 22,4% привезённых дров. Сколько ещё надо распилить дров, чтобы они составляли 33,6% привезённых дров?
Когда изготовили 756 деталей, то выполнили план на 72%. Сколько деталей должны изготовить по плану?
Теплоход на подводных крыльях прошёл расстояние между двумя пристанями со средней скоростью 60 км/ч за 2,5 ч. За сколько времени пройдёт это расстояние теплоход, если будет идти со скоростью 50 км/ч?
На изготовление 8 деталей требуется г серебра. Сколько серебра потребуется на изготовление 12 таких деталей?
24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с той же производительностью?
0,7 кг печенья автомат расфасовывает за 2,03 мин. За сколько минут этот автомат расфасует 1,5 кг печенья? Сколько печенья он может расфасовать за 1,16 минут?
Расфасовали 0,9 т крупы, что составляет 46,8% всей крупы, привезённой в магазин. Сколько крупы надо ещё расфасовать, чтобы она составляла 65% привезённой крупы?
Когда израсходовали 78,4 кг картофеля, то оказалось, что израсходовано 24,5% всего запаса. Сколько кг картофеля было запасено?
Теплоход «Ракета» прошёл расстояние между пристанями со скоростью 50 км/ч за 4,8 ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,2 ч?
На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?
На участке дороги бетонные плиты длиной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?
За 0,7 кг заплатили 280 рублей. Сколько надо заплатить за 1,9 кг такого мяса? Сколько мяса можно купить на 420 рублей?
Рассортировали 13,6 т зерна, что составило 54% имевшегося зерна. Сколько тонн зерна надо ещё рассортировать, чтобы осталось лишь 19% имевшего зерна?
Когда сдали на элеватор 2,1 тыс. т пшеницы, то оказалось, что план сдачи зерна выполнен на 105%. Сколько тонн зерна надо было сдать по плану?
Всадник, двигаясь со скоростью 18 км/ч, преодолел некоторое расстояние за 1,5 ч. За какое время проедет это расстояние экипаж, скорость которого на 3 км/ч меньше скорости всадника?
Для изготовления 10 деталей требуется кг металла. Сколько металла пойдёт на изготовление 12 таких деталей?
Для перевозки груза автомобилю, грузоподъёмностью 6 т надо сделать 10 рейсов. Сколько придётся сделать рейсов автомобилю, грузоподъёмность которого на 2 т меньше, чтобы перевезти этот груз?
4
Источник
Чтобы узнать название темы урока, обратите внимание на картинку.
Попробуйте отгадать ребус.

На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.
Слово «пропорция» (proportio) в переводе с латинского – соразмерность, отношение частей (соотношение).
В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.
Пропорции применяли с древности при решении различных задач.
Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.
Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.
В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.
В швейных технологиях – для изменения размеров выкройки изделия до нужного размера.
В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.
В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.
В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.

Разберем, что же такое пропорция в математическом понимании.
Возьмем два отношения: (mathbf{frac{36}{9}}) и (mathbf{frac{12}{3}}) и эти отношения равны, так как (mathbf{36div9=4}) и (mathbf{12div3=4}), значит (mathbf{frac{36}{9}= frac{12}{3}})
Равенство двух отношений называют пропорцией.

С помощью букв запишем пропорцию из двух отношений так: (mathbf{adiv b= cdiv d }) или (mathbf{frac{a}{b}= frac{c}{d}}).
Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».
Все члены пропорции не равны нулю: (mathbf{aneq 0, bneq 0, cneq 0, dneq 0}).
Если внимательно посмотреть на пропорцию (mathbf{{a}div{b}= {c}div{d}}), то можно заметить будто величины a и d стоят по краям равенства, а величины b и c в середине пропорции, в связи с этим легко запомнить, что:
Числа a и d называют крайними членами пропорции.
Числа b и c называют средними членами пропорции.

У меня есть дополнительная информация к этой части урока!
Закрыть
В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.
Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.
В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.
Обозначают число «золотого сечения» математической буквой (mathbf{varphi}) (фи).
Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».
Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».
Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».
Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».
Спиралевидная форма ракушек тоже описывается числом (mathbf{varphi}) (фи).


«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека
Теория отношений и пропорции изложена в «Началах» древнегреческого математика Эвклида (3 век до н.э.), в этом же труде было подробно описано и доказано основное свойство пропорции.
Давайте рассмотрим, какими же свойствами обладает пропорция и каким правилам подчиняется.
Пропорция, в которой произведение крайних членов равно произведению средних членов, является верной пропорцией.
Обратное утверждение так же является истинным.
Если произведение крайних членов равно произведению средних членов, то пропорция верна.
Данное свойство пропорции – это основное свойство пропорции.
Найдем произведение крайних членов пропорции (mathbf{adiv b= cdiv d }) и произведение средних членов этой пропорции, получим: (mathbf{acdot d= ccdot b }).
Пример
Дана пропорция (mathbf{frac{3}{5}= frac{6}{10}}), где числа 3, 10 – это крайние члены этой пропорции, 5, 6 – это средние члены пропорции.
По основному свойству пропорции
(mathbf{3cdot 10= 5cdot 6 = 30 }), значит пропорция (mathbf{frac{3}{5}= frac{6}{10}}) верная.
Если в верной пропорции поменять местами средние члены или крайние члены, то получатся новые верные пропорции.
Дополнительный материал
Пропорция обладает рядом других интересных свойств.
Так как члены пропорции отличны от нуля, то справедливо следующее: если в пропорции перевернуть отношения, то в результате получится тоже верная пропорция.
(mathbf{frac{a}{b}= frac{c}{d}})перевернем отношения и получим (mathbf{frac{b}{a}= frac{d}{c}})
Пример
(mathbf{frac{12}{2}= frac{6}{1}}) перевернем отношения и получим (mathbf{frac{2}{12}= frac{1}{6}}) , проверим полученное равенство.
По основному свойству пропорции (mathbf{2cdot 6= 12cdot 1 = 12 })
Новая пропорция (mathbf{frac{2}{12}= frac{1}{6}}) является верной.
При решении задач иногда используют правило увеличения и уменьшения пропорции.
Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то равенство сохранится в следующих случаях:
Увеличение пропорции: (mathbf{frac{a + b}{b}= frac{c + d}{d}}),
Уменьшение пропорции: (mathbf{frac{a – b}{b}= frac{c – d}{d}}).
Пропорция обладает еще одним свойством: нахождение пропорции сложением или вычитанием членов пропорции.
Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то справедливо
составление пропорции сложением (mathbf{frac{a + c}{b + d}= frac{a}{b} = frac{c}{d}})
составление пропорции вычитанием (mathbf{frac{a – c}{b – d}= frac{a}{b} = frac{c}{d}})
Применяя основное свойство пропорции, можно найти неизвестный член этой пропорции.
Решить пропорцию – это значит найти средний или крайний член пропорции.
Для решения пропорции с неизвестным крайним членом, при условии, что все остальные члены пропорции определены, необходимо умножить средние члены пропорции и полученный результат разделить на известный крайний член пропорции.
Пример 1
(mathbf{frac{a}{2}= frac{6}{1}})
решите пропорцию, найдя значение крайнего члена пропорции (a).
(mathbf{a = frac{2 cdot 6}{1}= 12})
Подставьте значение крайнего члена (а) в пропорцию
(mathbf{frac{12}{2} = frac{6}{1}= 6}) получили верную пропорцию.
Для решения пропорции с неизвестным средним членом, при условии, что все остальные члены пропорции определены, необходимо умножить крайние члены пропорции и полученный результат разделить на известный средний член пропорции.
Пример 2
(mathbf{frac{12}{b}= frac{6}{1}}) решим пропорцию, найдем значение среднего члена пропорции (b)
(mathbf{b = frac{12 cdot 1}{6}= 2})
Подставим значение среднего члена (b) в пропорцию
(mathbf{frac{12}{2} = frac{6}{1}= 6}) получили верную пропорцию.
Часто для решения пропорции используют способ «крест-накрест».
Чтобы вычислить неизвестный член пропорции, нужно перемножить известные члены пропорции, находящиеся на диагональной линии, а затем разделить результат на оставшееся известное число, находящееся на диагональной линии с неизвестным членом пропорции.

Пример 3
(mathbf{frac{8}{2}= frac{x}{8}}) , где x– неизвестный член пропорции,
(mathbf{8 cdot 8 = 64}) перемножили известные значения членов пропорции, находящиеся по диагонали в этой пропорции.
Полученный результат делим на известный член, находящийся по диагонали с неизвестным.
(mathbf{x = 64 div 2 = 32})
Получили пропорцию (mathbf{frac{8}{2} = frac{32}{8}= 4}), пропорция верна
К решению пропорции сводятся многие математические задачи и уравнения.
Рассмотрим некоторые из них.
Задача 1
Решите уравнение (mathbf{frac{y}{1,5}= frac{4}{3}})
Решение:
Найдем неизвестный член пропорции y, применив основное свойство пропорции.
Составим уравнение и решим его
(mathbf{3 cdot y = 1,5 cdot 4})
(mathbf{y = frac{1,5 cdot 4}{3}})
(mathbf{y = frac{6}{3}})
(mathbf{y = 2})
Ответ: (mathbf{y = 2})
Задача 2
На товар была сделана скидка 150 рублей, что составляет 15% от первоначальной цены товара.
Чему равна первоначальная цена товара?
Решение:
В задачах на проценты целое принимают за 100% или 1.
Неизвестную величину обозначают буквой (чаще всего x или y).
Величины в задаче должны быть приведены в одинаковые единицы измерения.
Модель решения задач с процентами при помощи пропорции можно представить в виде таблицы:

Или с помощью логической схемы

В результате пропорция получается такого вида:

Исходя из вышеизложенного, решение задачи будет выглядеть так:
Пусть x (рублей) – первоначальная цена товара, она составляет 100%.
Часть от целого (первоначальной цены) = 15%
Составим условную запись задачи:
x (руб.) – 100%
150 (руб.) – 15%
Составим пропорцию:(mathbf{frac{x}{150}= frac{100}{15}})
По основному свойству пропорции решим уравнение.
(mathbf{x = frac{150 cdot 100}{15}})
(mathbf{x = 1000 (руб.)}) первоначальная цена товара.
Ответ: (mathbf{x = 1000 (руб.)})
Задача 3
За 5 кг Муки заплатили 195 рублей. Какова стоимость 3 кг этой муки?
Решение:
Пусть x (рублей)- стоимость 3 кг муки.
Составим условную запись задачи.
5 (кг)- 195 (руб)
3 (кг)- x (руб)
Составим пропорцию: (mathbf{frac{5}{3}= frac{195}{x}})
По основному свойству пропорции решим уравнение:
(mathbf{x = frac{3 cdot 195}{5}})
(mathbf{x = 117 (руб.)}) стоят 3 кг муки.
Ответ: (mathbf{x = 117 (руб)})
Пройти тест
Источник
