Какие свойства электропривода характеризует маховый момент

Тема: Определение момента инерции и махового момента электрического привода методом свободного выбега
Цель работы.
Определить момент инерции и маховой момент электропривода, приобрести практические навыки в опытном определении момента инерции и махового момента электропривода; получить экспериментальное подтверждение теоретическим сведениям.
Программа работы
1. Ознакомиться с устройством лабораторной установки; записать паспортные данные электрических машин и измерительных приборов.
2. Собрать схему по рис. 26.1 и после проверки ее преподавателем выполнить опыт холостого хода.

3. Снять данные и построить график «Кривая выбега» агрегата n = f(t).
4. Используя результаты опытов (п. 2 и 3), определить общий момент инерции и маховой момент агрегата.
5. Составить отчет и сделать заключение о проделанной работе
Подготовка к работе
1. Повторить теоретический материал: статический и динамический моменты инерции; основное уравнение движения электропривода; момент инерции и маховой момент электропривода; приведение момента инерции и махового момента электропривода к частоте вращения вала двигателя.
2. Подготовить в рабочей тетради таблицы для занесения результатов опытов и координатную сетку для построения графика.
Основные понятия и сведения из теории.
При установившемся режиме работы электропривода, т. е. при постоянной его частоте вращения, мощность, развиваемая электродвигателем, расходуется на преодоление лишь только статической нагрузки. Если же в электроприводе наступил переходный режим, и он стал работать с переменной частотой вращения, то мощность электродвигателя расходуется не только на статическую, но и динамическую нагрузки.
Статическая нагрузка обусловлена двумя факторами: моментом статического сопротивления на валу рабочего механизма и силами сопротивления в передачах, соединяющих вал электродвигателя с выходным валом рабочего механизма (рабочей машины) динамическая нагрузка электропривода определяется динамическим моментом Мд обусловленным изменением скорости движения всех элементов системы электропривода.
Уравнение движения электропривода устанавливает связь между моментами, действующими на вал электродвигателя: моментом М2 развиваемым электродвигателем на его валу, моментом стати ческой нагрузки Мс, и динамическим моментом Мд:
М2= Мс± Мд
Знак плюс в этом выражении соответствует процессу ускорения (нарастанию скорости) электропривода, а знак минус замедлению (убыванию скорости). Момент статической нагрузки, соответствующий установившемуся режиму работы электропривода (не изменой частоте вращения), можно представить в виде суммы моментов — момента статического сопротивления механизма Мс.м, обусловленного полезной работой механизма (например, работой по подъему груза), и момента трения Мтр, вызванного силами трения в механизме:
Мс = Мс.м + Мтр
Момент трения можно учесть введением в уравнение значений КПД рабочего механизма и КПД передаточного устройства (редуктора) ηред. В этом случае момент статического сопротивления механизма (Н·м)
Мс = Мс.м / η
где η = ηр.м.· ηред
Динамический момент Мд возникает под влиянием ускорений при изменениях скорости движения, для электропривода с вращательным движением динамический момент (Н·м)
Мд = Ј·(dω/dt),
где
Ј- момент инерции вращающегося тела относительно оси вращения, кг·м2
ω- угловая скорость вращения этого тела, рад/с.
Используя выражения, получим уравнение движения электропривода:
М2 = Мс + Мд = (Мс.м / η) + Ј·(dω/dt)
Обычно приводной двигатель соединяется с рабочим механизмом промежуточным передаточным устройством, изменяющим на вращения и передаваемый момент. Таким устройством чаще всего является редуктор с КПД и передаточным отношением i=ωд/ωмех, угловые скорости вращения валов двигателя и рабочего механизма соответственно.
Для того, чтобы избежать трудоемкого решения нескольких уравнений движения для различных элементов электропривода с разными угловыми скоростями движения, все моменты сопротивления и моменты инерции различных элементов, образующих систему электропривода, приводят к какой-либо одной скорости движения- обычно к угловой скорости вращения вала электродвигателя. Другими словами, реальная система электропривода, элементы которой вращаются с разными угловыми скоростями, заменяется упрощенной системой, у которой вся движущаяся масса сосредоточена на одном валу в вращается с угловой скоростью. В этом случае приведенное значение статического момента сопротивления механизма имеет вид
М‘с.м.= Мс.м./ η·i
где i=ωд/ωмех – передаточное отношение редуктора.
Общий момент инерции системы электропривода определяется суммой моментов инерции: момента инерции Јд вращающихся частей электродвигателя и расположенных на его валу устройств (например, соединительной муфты) и момента инерции Ј’ приведенного к угловой скорости вала двигателя передающего устройства (редуктор) и рабочего механизма:
Јобщ = Јд + Ј‘
Приведенный момент инерции Ј’ определяется суммой приведенных значений моментов инерции всех элементов электропривода, вращающихся с угловой скоростью, отличающейся от угловой скорости вращения вала двигателя ωд;
где i, – передаточные отношения на разных ступенях угловых скоростей вращения.
Мерой инерции вращающихся тел является также маховой момент, связанный с моментом инерции Ј зависимостью
GD2 = 4·g·J
где G – сила тяжести вращающегося тела, Н; D- диаметр вращения, м; g=9,81 м/с — ускорение свободного падения (является коэффициентом, связывающим единицы измерения — ньютоны и килограммы: 1 кг = 9,81 Н); Ј— момент инерции, кг·м2
GD2 = 4·Ј
В данной работе рассматривается один из методов экспериментального определения общего момента инерции и общего махового момента системы электропривода, называемый методом свободного выбега (самоторможения). Выбег — это неустановившееся движение (по инерции) подвижных частей системы электропривода после отключения двигателя за счет кинетической энергии этих частей.
Сущность метода выбега состоит в следующем. Исследуемый агрегат, включающий двигатель и механически соединенные с ним элементы, разгоняется до некоторой установившейся частоты вращения в режиме холостого хода. После этого двигатель отключают от сети, и наступает процесс самопроизвольного торможения, т. е. торможения исключительно за счет внутренних сил трения (трения в подшипниках, трения щеток о коллектор или контактные кольца двигателя, трение в других элементах электропривода). На преодоление этих сил трения затрачивается кинетическая энергия (Дж), запасенная во вращающихся частях агрегата:
А = Jобщ·ω2д 0 /2
С другой стороны, эта энергия может быть определена как произведение мощности, затраченной на приведение во вращение системы электропривода в режиме холостого хода Рвр на время t0
A=Pвр.0·t
Приравняв, получим выражение общего момента инерции (кг·м2)
Jобщ = 2·Pвр.0·t / ω2д.0
Переходя к частоте вращения двигателя в режиме холостого хода и учитывая, что ω= 0,105 n, получим
Јобщ = 182 Рвр.0·t / n2д.0
По найденному значению общего момента инерции вращающихся частей системы электропривода Јобщ, воспользовавшись, зависимостью, определяют маховый момент агрегата (н·м2).
GD2 = 4·g·Jобщ = 7142·Pвр.·t /n2д.
Значения мощности и времени, определяют экспериментально, выполнив опыт холостого хода, опыт свободного выбега и построив кривую выбега.
Порядок выполнения работы
Опыт холостого хода.
Двигатель включают в сеть при номинальном напряжении сети. Регулировочным реостатом устанавливают частоту вращения. После того как частота вращения агрегата достигнет установившегося значения, снимают показания приборов и заносят их в табл.1. Необходимые вычисления, выполняют по формулам:
мощность в цепи якоря двигателя (Вт)
Р = U·Iα0;
электрические потери в обмотках цепи якоря двигателя (Вт)
Pэ.α = I2α0·∑r
Где ∑r = rα +rд.п + ….
— сумма сопротивлений обмоток в цепи якоря двигателя при температуре окружающей среды, если опыт проводился на «холодном двигателе), Ом;
электрические потери в щеточном контакте (Вт)
Pэ.щ. = Iα0·∆Uщ
где ∆Uщ – падение напряжения в контакте щеток (принимают = 2В)
Все полученные значения величин заносят в табл. 26.1 и определяют мощность, затраченную на вращение агрегата в режиме холостого хода (Вт)
Таблица № 1.
График кривая выбега.
После снятия показаний приборов при опыте холостого хода отключают двигатель от сети и одновременно включают секундомер. В процессе выбега агрегата, т. е. его вращения по инерции, необходимо 6— 8 раз измерить частоту вращения с одновременным фиксированием времени каждого замера по секундомеру. Первый замер частоты вращения делают в момент отключения двигателя, т. е. в момент времени О, а последний в момент полной остановки агрегата, т. е. при n = О. Особенно внимательно следует отнестись к измерениям при первых трех замерах, следующих непосредственно за отключением двигателя, так как

эти замеры в значительной степени влияют на точность результата эксперимента. Показания приборов заносят в табл. 2. затем строят график « кривая выбега» (рис. 26.2).
Таблица № 2
Чтобы воспользоваться выражением для определения общего момента инерции агрегата, необходимо определить постоянную времени выбега. С этой целью на графике «кривая выбега» проводят касательную к начальной части кривой в точке А (см. рис. 26.2) сечения с осью абсцисс в точке В. Полученный таким отрезок ОВ на оси абсцисс и определит время, которое заносят в табл. 3. В эту же таблицу записывают значения и Pвр.0 и nд.0 из табл. 1, а затем определяют общий момент инерции агрегата и маховой момент.
Таблица № 3
Анализ результатов лабораторной работы
Анализируя результаты лабораторной работы, необходимо иметь в виду следующее. При расчете момента инерции в выражении предусмотрена подстановка значения мощности, затраченной исключительно на приведение во вращение агрегата с частотой вращения nд.0 , т. е. мощности механических потерь Рмех. Что же касается значения мощности Рвр.0, определяемой по формуле, то она помимо мощности механических потерь включает в себя и мощность Рм, т.е.
Рвр.0 =Рм + Рмех
Следует заметить, что исследованию подвергается агрегат, состоящий из двух электрических машин, поэтому магнитные потери происходят лишь в одной из них (двигателе), а механические потери одновременно в двух машинах. По этой причине доля магнитных потерь в общей сумме потерь
Рвр.0 =Рм + Рмех.д + Рмех.г
становится малозначительной. Если же учесть, что в реальных условиях система электропривода содержит помимо рабочей машины еще и передаточное устройство (редуктор), в котором также имеют место механические потери, то ошибка метода свободного выбега становится практически незаметной.
Контрольные вопросы
1. На какие свойства электропривода влияет величина момента инерции и махового момента?
2. Что такое маховой момент и какова его зависимость от момента инерции системы электропривода?
3. На чем основан метод свободного выбега для определения момента инерции системы электропривода?
4. Как изменится время выбега агрегата, если на валу двигателя установить маховик?
5. Что представляет собой кривая выбега, и каков порядок снятия данных для ее построения?
6. Что называется электроприводом?
7. Схема структуры электропривода?
8. Статический и динамический моменты?
9. Основные режимы работы электродвигателя?
10. Момент инерции?
Источник
Âûáîð ýëåêòðîïðèâîäà îïðåäåëÿåòñÿ òðåáîâàíèÿìè ðàáî÷åé ìàøèíû. Ýëåêòðîïðèâîä äîëæåí îáåñïå÷èòü âûïîëíåíèå ðàáî÷åé ìàøèíîé çàäàííîé òåõíîëîãèè ïðè âñåõ âîçìîæíûõ ðåæèìàõ: ïóñêà, ïðèåìà è ñáðîñà íàãðóçêè, òîðìîæåíèÿ, èçìåíåíèÿ ñêîðîñòè, ïîñòîÿííîé íàãðóçêè. Õàðàêòåð ïðîòåêàíèÿ ýòèõ ðåæèìîâ â ïåðâóþ î÷åðåäü îïðåäåëÿåòñÿ ìåõàíè÷åñêèìè ñâîéñòâàìè äâèãàòåëÿ è ðàáî÷åé ìàøèíû. Îäíèì èç îñíîâíûõ êðèòåðèåâ îöåíêè ìåõàíè÷åñêèõ ñâîéñòâ êàê äâèãàòåëÿ, òàê è.ðàáî÷åé ìàøèíû ñëóæàò èõ ìåõàíè÷åñêèå õàðàêòåðèñòèêè.
Ìåõàíè÷åñêèå õàðàêòåðèñòèêè ýëåêòðîäâèãàòåëåé
Ìåõàíè÷åñêîé õàðàêòåðèñòèêîé ýëåêòðîäâèãàòåëÿ íàçûâàåòñÿ çàâèñèìîñòü ñêîðîñòè âðàùåíèÿ âàëà îò ðàçâèâàåìîãî äâèãàòåëåì ìîìåíòà ω=φ(Ìä) èëè n =f(Ìä), ãäå ω – óãëîâàÿ ñêîðîñòü âðàùåíèÿ âàëà, ðàä/ñ, n – ñêîðîñòü âðàùåíèÿ âàëà, îá/ìèí.
Ìåõàíè÷åñêàÿ õàðàêòåðèñòèêà äâèãàòåëÿ íàçûâàåòñÿ åñòåñòâåííîé, åñëè çàâèñèìîñòü n = f (Ì) ïîëó÷åíà ïðè íîìèíàëüíûõ ïàðàìåòðàõ ïèòàþùåé ñåòè, íîðìàëüíîé ñõåìå âêëþ÷åíèÿ è áåç äîáàâî÷íûõ ñîïðîòèâëåíèé â öåïè äâèãàòåëÿ.
Ïðè íàëè÷èè äîáàâî÷íûõ ñîïðîòèâëåíèé èëè ïèòàíèè äâèãàòåëÿ îò ñåòè ñ íàïðÿæåíèåì èëè ÷àñòîòîé, îòëè÷íûìè îò íîìèíàëüíûõ, ìåõàíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëÿ áóäóò íàçûâàòüñÿ èñêóññòâåííûìè. Î÷åâèäíî, ÷òî èñêóññòâåííûõ õàðàêòåðèñòèê äâèãàòåëü èìååò áåñ÷èñëåííîå ìíîæåñòâî, à åñòåñòâåííóþ – òîëüêî îäíó.
Áîëüøèíñòâî ýëåêòðîäâèãàòåëåé ïîä íàãðóçêîé ïðè óâåëè÷åíèè ìîìåíòà ñíèæàåò ñêîðîñòü âðàùåíèÿ. Õàðàêòåðèñòèêó â ýòîì ñëó÷àå íàçûâàþò ïàäàþùåé. Ñòåïåíü èçìåíåíèÿ ñêîðîñòè äâèãàòåëÿ ïðè èçìåíåíèè ìîìåíòà îöåíèâàþò òàê íàçûâàåìîé æåñòêîñòüþ ìåõàíè÷åñêîé õàðàêòåðèñòèêè, êîòîðóþ îïðåäåëÿþò îòíîøåíèåì α = ΔÌ/Δω èëè α = ΔÌ/Δn
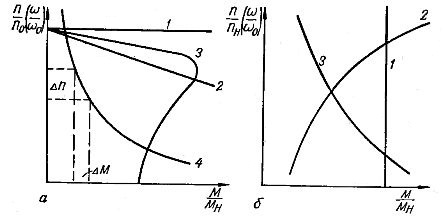
Ðèñ. 1. Ðàçëè÷íûå âèäû ìåõàíè÷åñêèõ õàðàêòåðèñòèê: à – ýëåêòðîäâèãàòåëåé, á – ïðîèçâîäñòâåííûõ ìàøèí.
Âåëè÷èíû èçìåíåíèÿ ìîìåíòà è ïàäåíèÿ ñêîðîñòè ïðè îïðåäåëåíèè æåñòêîñòè áåðóò îáû÷íî â îòíîñèòåëüíûõ åäèíèöàõ. Ýòî äàåò âîçìîæíîñòü ñðàâíèâàòü õàðàêòåðèñòèêè äâèãàòåëåé ðàçëè÷íîãî âèäà.
 çàâèñèìîñòè îò ñòåïåíè æåñòêîñòè âñå ìåõàíè÷åñêèå õàðàêòåðèñòèêè äâèãàòåëåé ïîäðàçäåëÿþò íà ñëåäóþùèå ãðóïïû.
1. Àáñîëþòíî æåñòêèå õàðàêòåðèñòèêè ñ âåëè÷èíîé æåñòêîñòè α = ∞. Òàêèå ìåõàíè÷åñêèå õàðàêòåðèñòèêè (êðèâàÿ 1, ðèñ. 1, à) ñî ñòðîãî ïîñòîÿííîé ñêîðîñòüþ âðàùåíèÿ èìåþò ñèíõðîííûå äâèãàòåëè.
2. Æåñòêèå õàðàêòåðèñòèêè ñî ñðàâíèòåëüíî íåáîëüøèì ïàäåíèåì ñêîðîñòè ïðè óâåëè÷åíèè ìîìåíòà è α = 40 – 10. Ê ýòîé ãðóïïå îòíîñÿòñÿ åñòåñòâåííûå õàðàêòåðèñòèêè äâèãàòåëåé ïîñòîÿííîãî òîêà ñ íåçàâèñèìûì âîçáóæäåíèåì (êðèâàÿ 2) è õàðàêòåðèñòèêè àñèíõðîííûõ äâèãàòåëåé â ïðåäåëàõ ëèíåéíîãî ó÷àñòêà (êðèâàÿ 3).
3. Ìÿãêèå ìåõàíè÷åñêèå õàðàêòåðèñòèêè ñ áîëüøèì îòíîñèòåëüíûì ïàäåíèåì ñêîðîñòè ïðè óâåëè÷åíèè ìîìåíòà è ñ æåñòêîñòüþ äî α = 10. Òàêèå õàðàêòåðèñòèêè èìåþò äâèãàòåëè ïîñòîÿííîãî òîêà ñ ïîñëåäîâàòåëüíûì âîçáóæäåíèåì (êðèâàÿ 4), äâèãàòåëè ñ íåçàâèñèìûì âîçáóæäåíèåì ñ áîëüøèì ñîïðîòèâëåíèåì â öåïè ÿêîðÿ è àñèíõðîííûå äâèãàòåëè ñ äîáàâî÷íûìè ñîïðîòèâëåíèÿìè â öåïè ðîòîðà.
Ïðè ðàáîòå ýëåêòðîïðèâîäà äëÿ ïðåîäîëåíèÿ ñîïðîòèâëåíèÿ ðàáî÷åé ìàøèíû äâèãàòåëü äîëæåí ðàçâèâàòü îïðåäåëåííûé ìîìåíò. Ïîýòîìó ïðè âûáîðå äâèãàòåëÿ íåîáõîäèìî âûÿâèòü ïðåæäå âñåãî ñîîòâåòñòâèå õàðàêòåðèñòèê äâèãàòåëÿ è ðàáî÷åé ìàøèíû.

Ìåõàíè÷åñêèå õàðàêòåðèñòèêè ðàáî÷èõ ìàøèí
Ìåõàíè÷åñêîé õàðàêòåðèñòèêîé ðàáî÷åé ìàøèíû íàçûâàþò çàâèñèìîñòü ìîìåíòà ñòàòè÷åñêèõ ñîïðîòèâëåíèé ìàøèíû îò ñêîðîñòè âðàùåíèÿ ïðèâîäíîãî âàëà. Ýòó çàâèñèìîñòü äëÿ óäîáñòâà ñîâìåñòíîãî ïîñòðîåíèÿ âûðàæàþò îáû÷íî òàê æå, êàê è õàðàêòåðèñòèêó äâèãàòåëÿ, â âèäå ω=φ(Ìñ) èëè n =f(Ìñ).
Ìîìåíò ñòàòè÷åñêèõ ñîïðîòèâëåíèé Ìñ, èëè ñîêðàùåííî ñòàòè÷åñêèé ìîìåíò, ïðåäñòàâëÿåò ñîáîé ìîìåíò ñîïðîòèâëåíèÿ, ñîçäàâàåìûé ìàøèíîé íà ïðèâîäíîì âàëó â ñòàòè÷åñêîì (óñòàíîâèâøåìñÿ) ðåæèìå, êîãäà ñêîðîñòü íå èçìåíÿåòñÿ.
Ìåõàíè÷åñêóþ õàðàêòåðèñòèêó ìàøèíû ìîæíî ïîëó÷èòü îïûòíûì ïóòåì èëè ðàñ÷åòîì, åñëè èçâåñòíî ðàñïðåäåëåíèå ñòàòè÷åñêèõ óñèëèé èëè ìîìåíòîâ ïî ýëåìåíòàì êèíåìàòè÷åñêîé ñõåìû. Ñòàòè÷åñêèå ìîìåíòû ìàøèí ìîãóò çàâèñåòü íå òîëüêî îò ñêîðîñòè, íî è îò äðóãèõ âåëè÷èí, ïîýòîìó ïðè ïðàêòè÷åñêèõ ðàñ÷åòàõ ýëåêòðîïðèâîäîâ íåîáõîäèìî ðàññìàòðèâàòü êàæäûé ñëó÷àé â îòäåëüíîñòè.
Ñòàòè÷åñêèå ìîìåíòû ðàçëè÷íûõ ðàáî÷èõ ìàøèí ïî õàðàêòåðó çàâèñèìîñòè èõ îò ñêîðîñòè (ìåõàíè÷åñêèå õàðàêòåðèñòèêè) ïîäðàçäåëÿþò íà ãðóïïû. Íàèáîëåå ÷àñòî âñòðå÷àþùèåñÿ íà ïðàêòèêå èç íèõ ñëåäóþùèå.
1. Ñòàòè÷åñêèé ìîìåíò ìàëî çàâèñèò èëè ïðàêòè÷åñêè íå çàâèñèò îò ñêîðîñòè (êðèâàÿ 1, ðèñ. 2, á). Òàêèå õàðàêòåðèñòèêè èìåþò ïîäúåìíûå ìåõàíèçìû, êðàíû, ëåáåäêè, òåëüôåðû, à òàêæå ëåíòî÷íûå òðàíñïîðòåðû ïðè ïîñòîÿííîé íàãðóçêå.
2. Ñòàòè÷åñêèé ìîìåíò ìàøèíû âîçðàñòàåò ïðîïîðöèîíàëüíî êâàäðàòó ñêîðîñòè (êðèâàÿ 2). Ýòó õàðàêòåðèñòèêó, òèïè÷íóþ äëÿ îñåâûõ âåíòèëÿòîðîâ, íàçûâàþò âåíòèëÿòîðíîé õàðàêòåðèñòèêîé è àíàëèòè÷åñêè ïðåäñòàâëÿþò â âèäå ôîðìóëû: Mc = Mî+kn2, ãäå Ìî – íà÷àëüíûé ñòàòè÷åñêèé ìîìåíò, îáóñëîâëåííûé ÷àùå âñåãî ñèëàìè òðåíèÿ, êîòîðûå îáû÷íî íå çàâèñÿò îò ñêîðîñòè, k – îïûòíûé êîýôôèöèåíò. Êðîìå âåíòèëÿòîðîâ, âåíòèëÿòîðíûìè õàðàêòåðèñòèêàìè îáëàäàþò öåíòðîáåæíûå è âèõðåâûå íàñîñû, ñåïàðàòîðû, öåíòðèôóãè, ãðåáíûå âèíòû, òóðáîêîìïðåññîðû è áàðàáàíû ìîëîòèëîê íà õîëîñòîì õîäó.
3. Ñòàòè÷åñêèé ìîìåíò óìåíüøàåòñÿ ïðè óâåëè÷åíèè ñêîðîñòè (êðèâàÿ 3). Ê ýòîé ãðóïïå îòíîñÿòñÿ õàðàêòåðèñòèêè íåêîòîðûõ òðàíñïîðòåðíûõ ìåõàíèçìîâ è íåêîòîðûõ ìåòàëëîðåæóùèõ ñòàíêîâ.
4. Ñòàòè÷åñêèé ìîìåíò èçìåíÿåòñÿ îò ñêîðîñòè íåîäíîçíà÷íî, ñ ðåçêèì ïåðåõîäîì, îáóñëîâëåííûì îñîáåííîñòüþ òåõíîëîãè÷åñêîãî ïðîöåññà. Õàðàêòåðèñòèêè ýòîé ãðóïïû èìåþò ìàøèíû, ðàáîòàþùèå ñ ÷àñòûìè áîëüøèìè ïåðåãðóçêàìè, êîòîðûå èíîãäà ïðèâîäÿò ê ïîëíîé îñòàíîâêå. Íàïðèìåð, ìåõàíèçì ÷åðïàíèÿ îäíîêîâøîâîãî ýêñêàâàòîðà, ñêðåáêîâûé òðàíñïîðòåð, ðàáîòàþùèé ïîä çàâàëîì òðàíñïîðòèðóåìîé ìàññû, äðîáèëêè è äðóãèå ìàøèíû.
Êðîìå ïåðå÷èñëåííûõ, íà ïðàêòèêå âñòðå÷àþòñÿ è äðóãèå âèäû ìåõàíè÷åñêèõ õàðàêòåðèñòèê ìàøèí, íàïðèìåð ïîðøíåâûõ íàñîñîâ è êîìïðåññîðîâ, ñòàòè÷åñêèå ìîìåíòû êîòîðûõ çàâèñÿò îò ïóòè.
Источник
Иногда возникает необходимость приведения маховых масс электропривода к одной оси. Это приводит к удобству расчета системы электропривода, так как все моменты инерции системы приводятся как правило к валу машины.
Для начала разберемся что такое момент инерции относительно оси – это сумма произведений масс отдельных частей тела, умноженного на квадрат расстояния этой же части тела до оси вращения, которая берется для всего тела:
На практике, как правило, момент инерции довольно часто выражают как произведение квадрата радиуса инерции на массу тела:
m – общая масса всего тела, выраженная в кГсек2/м;
p – радиус инерции тела, выражен он в м;
Радиус инерции – расстояние от оси вращения, которая проходит через центр тяжести объекта, на котором нужно поместить массу объекта, которая будет сосредоточена в одной точке, чтоб она удовлетворяла равенству:
Значения радиусов инерции простейших геометрических тел приведены ниже. Используя формулы приведенные ниже и при условии известности массы тела, можно вычислить момент инерции тела по формулам, приведенным выше:


Если геометрические тела не сложные, то момент инерции можно приблизительно определить как сумму таких моментов отдельных тел , взятых относительно оси вращения. Как пример – момент инерции (далее J) маховика будет равен сумме J спиц, обода и втулки. В случаях, когда точное вычисление J представляется затруднительным, могут оперировать приближенными величинами. Иногда для маховика определяют J обода и прибавляют от 8% до 15% для учета маховых масс спиц. В случае червяка J ротора зубцов принимается 40% J пологого цилиндра соответствующих размеров. Червячное или зубчатое колесо учитывается как полый цилиндр. К полученной величине добавляют 25% для спиц и втулки. Если для зубчатого колеса известны только вес и шаг зацепления, то J могут определять как произведение 60% всего веса на квадрат радиуса длительной окружности.
Приведенный момент инерции (Jпр) входит в уравнение движения электропривода. Jпр – это J простейшей системы, которая состоит из элементов, которые вращаются со скоростью вала или оси, к которой производят приведение, и при этом запас кинетической энергии приведенной системы равен запасу кинетической энергии реальной системы.
Ниже показана реальная система и приведенная
Реальная:

Приведенная:

В таком случае выполнится равенство:
Где: Jпр – приведенный момент инерции в валу электромашины;
J1, J2… Jn, ω1, ω2, ωn – моменты инерции и угловые скорости вращения механизмов или передач машины в соответствующих осях;
Jд, ωд – угловая скорость и момент инерции электродвигателя.
Отсюда очевидно, что:
Где: j1, j2, …, jn – передаточные числа между осями вращающихся звеньев и осью электромашины.
Отсюда следует, что Jпр вращающихся частей равен сумме J каждого отдельного элемента системы относительно своего вала, деленного на квадрат передаточного числа (j), между валом конкретного элемента и валом, к котором приводится момент инерции. Часто при определении Jпр системы его считают равным сумме моментов инерций ротора или якоря электрической машины и Jпр рабочего органа, а также J отдельных звеньев системы передаточного механизма учитывают с помощью увеличения J в δ раз, то есть:
Значение δ обычно лежит в пределах 1,1 ÷ 1,3.
В теории электропривода довольно часто встречается понятия махового момента – GD2, вместо моментов инерций. Если заменить в формуле приведенной выше массу m на вес G и ускорение свободного падения g, а радиус величины инерции p через ее диаметр D, получим следующее выражение:
GD2 выражается в кГм2. Очевидно, что для GD2 также существует соотношение, аналогичное выражению для J:
При введении вместо J в уравнение движение электропривода GD2 получим следующее выражение:
- При постоянном GD2:
- При переменном GD2:
Уравнения движения с использованием GD2 и числа оборотов в минуту могут казаться более удобными для применения на практике, так как скорость вращения вала машины обычно измеряют в оборотах в минуту — об/мин, GD2 – довольно часто публикуют в каталогах. Однако при использовании их следует помнить, что коэффициенты 375 и 7200 – числа, имеющие размерность ускорения. Без учета этих обстоятельств правые части этих выражений не будут иметь размерность момента. Поэтому при сложных расчетах рекомендуется использовать уравнение движения в форме или .
Источник
