Какие свойства поперечных волн
Что такое продольные и поперечные волны в физике
Волна — изменение характеристик физического поля или среды, способное удаляться от места возникновения или колебаться внутри ограниченной области пространства.
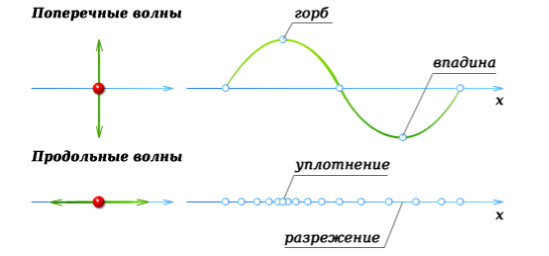
Продольные волны — волны, при которых частицы вещества колеблются вдоль направления распространения.
Поперечные волны — волны, при которых частицы вещества колеблются перпендикулярно направлению распространения.

В какой среде возможно распространение
И продольные, и поперечные волны относятся к упругим — возникающим только в упругой среде, обладающей свойством после деформации возвращаться к прежней форме.
Продольные волны возникают при сопротивлении среды изменению ее объема, их причина — деформация сжатия/растяжения (в твердой среде) или уплотнения/разрежения (в газах и жидкостях).
Чтобы узнать длину волны, нужно измерить расстояние между ближайшими точками сжатия или растяжения.
Продольные волны могут распространяться в любой среде: твердой, жидкой, газообразной. Во время этого процесса непрерывно изменяется давление в каждой точке среды.
В твердых телах продольные волны распространяются быстрее, чем поперечные. Для сравнения: продольная волна движется в стали со скоростью около 5900 м/с, поперечная — примерно 3250 м/с.
Поперечные волны возникают при сдвиге слоев среды относительно друг друга. Жидкости и газы не сопротивляются изменению формы, поэтому поперечные волны возможны только в твердых средах. Длина поперечной волны — расстояние между двумя ближайшими ее впадинами или горбами.
В каких направлениях совершаются колебания
- Продольная волна заставляет частицы среды колебаться у своих положений равновесия, и этот процесс перемещается параллельно направлению распространения волны. Частицы сдвигаются строго по одной линии.
- В поперечной волне колебания элементов происходят в направлениях, перпендикулярных направлению распространения волны. Среда стремится вернуть деформированные частицы на место, при этом на несмещенные частицы рядом со смещенными воздействуют силы упругости и отклоняют их от положения равновесия.
Из-за преломления или отражения продольные волны на границе раздела двух сред могут превращаться в поперечные, и наоборот.
Как характеризуется поперечная волна или волна сдвига
Чтобы однозначно характеризовать движение волны, необходимо составить ее уравнение. Для упругих волн уравнением служит функция координат и времени смещения частиц среды от их положений равновесия.
Общее уравнение гармонической плоской волны, распространяющейся вдоль положительного направления оси х в среде, которая не поглощает энергию:
(xi;(х,t);=;Acos;lbrackomega;times;(t;-;frac xv);+;varphi_0rbrack)

В этом выражении A — амплитуда волны, (omega) — циклическая частота, (varphi_0 )— начальная фаза волны, определяемая началом отсчета х и t.
Скорость поперечной волны зависит от погонной массы (mu) (массы единицы длины) и силы натяжения Т. Она рассчитывается по формуле (nu;=;sqrt{frac Тmu}.)
При распространении поперечной волны распределение возмущений среды происходит с нарушением симметрии.
Поляризация — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
Поляризация влияет на скорость распространения волны, часто используется для создания оптических эффектов, например, 3D-изображения.
Поляризация бывает круговой, эллиптической и линейной — в зависимости от формы кривой, вычерчиваемой концом вектора амплитуды. Круговая или эллиптическая поляризация может быть правой или левой, что определяется направлением вращения вектора.
Примеры продольных и поперечных волн
Все акустические волны — продольные. Звуки, слышимые человеком, находятся в диапазоне 17–20000 Гц. Ниже этого диапазона расположены инфразвуковые волны, выше — ультразвуковые. Также к продольным волнам относятся сейсмические Р-волны, возникающие во время землетрясений.
Увидеть колебания продольной волны без специальных приборов можно на примере пружины, подвешенной горизонтально. Если ударить по одному ее концу, несколько витков пружины сблизятся, затем разойдутся. Это колебание будет постепенно переходить от витка к витку по всей длине пружины.
Поперечные волны возникают в натянутых струнах или нитях. В случае электромагнитных волн поперечные колебания совершают векторы электрического и магнитного полей. Механического колебания не происходит, но электромагнитные волны, например, световые, тоже принято относить к поперечным.
Источник
С точки зрения физики, довольно интересным случаем является распространение частиц в перпендикулярном направлении от вызвавшего их колебания. Такое явление называется поперечными волнами. Их изучением занимался в своё время Максвелл, который сделал ошибочное предположение, что из поперечных колебаний состоит и свет. По сути, взаимодействие соседних элементов вызвано деформацией. При этом существовать они могут только в твёрдых телах.
Общие сведения
Волна представляет собой совокупность колебаний, передающихся через пространство за определённое время. Это определение применимо как к сферической, так и плоской среде. Появиться она может в газе, твёрдом теле, жидкости. В вакууме механической волны быть не может. Для её возникновения необходим источник, в качестве которого служит колеблющееся тело. Это движение вызывает деформацию, которой и сопутствует появление волны.
Все существующие возмущения принято разделять на два больших класса:
- Бегущие — это явления, при которых происходит передача энергии без изменения положения частичек.
- Упругие — волны, переносящие энергию и приводящие к возникновению упругости.
Последние колебания бывают продольными и поперечными. Первые характеризуются смещением элементов в направлении распространения возмущения. К их возникновению приводит сжатие или растяжение среды. То есть возникает реакция сопротивления среды на изменение объёма, например, звуковые волны, колебания в стержне. Поперечными же волнами называют деформацию, при которой происходит сдвиг слоёв среды. При таком роде колебаний наблюдается появление впадин и гребней. Возникать они могут только в твёрдом теле. Наиболее ярким примером поперечных волн может служить верёвка или леска в натянутом состоянии.
Рассматривая волновой процесс, принято считать, что частичка вещества представляет малый элемент объёма этого материала с размерами намного больше, чем расстояния между молекулами. Эти же частички для удобства принимаются за точки. Если в какой-либо среде заставить эту точку совершать колебание, то из-за связи её с другими частичками произойдёт передача возмущения. Этот процесс и принято называть в физике волной.
Волна может распространяться не только в направлении, перпендикулярном к плоскости среды, её колебания возможны и поперёк векторов электромагнитного поля. Поперечные колебания обладают поляризацией. Эта характеристика описывает поведение вектора возмущения в плоскости. Существует круговая, эллиптическая и линейная поляризация. Её вид зависит от формы кривой, описывающейся концом амплитудного вектора.
Механизм и закон распространения
Механические волны могут распространяться только в упругой среде. Вещество называется упругим, если после деформирования оно снова принимает свою начальную форму. Природа продольных колебаний связана с колебаниями частиц, остающихся в плоскости. При этом вызванные возмущения перпендикулярны направлению распространения волны. Называется такой эффект деформационным сдвигом. В газообразных веществах деформация может быть только объёмного характера. Поэтому отвечая на вопрос, в каких средах распространяются поперечные волны, однозначно можно ответить — только в твёрдых.
Основная задача изучения волн заключается в установлении закона, по которому они изменяются в течение времени и параметров, характеризующих возмущение. Одним из них является смещение S. Оно показывает, как изменяется положение точек относительно их нахождения в равновесии. Простым видом возмущений является гармоническая волна. Для её существования нужно, чтобы смещение всех частиц происходило с одинаковым периодом. Для этого необходимы условия, при которых источник колебаний сам будет совершать постоянные гармонические возмущения.
Пусть имеется бесконечная струна. По ней распространятся волна от источника, находящегося в её начале. Колебания, происходящие в ней, можно описать формулой: s0 = A0 * cos (wt + φ), где:
- A0 — амплитуда;
- Wt — изменение циклической частоты;
- φ – фаза в начальный период.
Если взять любую точку на струне и измерить колебания, то можно будет убедиться, что они отстают по фазе от генерирующего их источника. Эту задержку можно описать выражением: s0 = A * cos (w (t — t 1) + φ), где t1 — время, необходимое для того, чтобы точка волны пришла в исследуемое место. При этом если среда распространения не поглощает энергию, то амплитуда в произвольной точке и начальная будут равны.
Для описания одномерного колебания часто используется волновое число. Обозначается оно буквой k и находится через длину волны λ как k = 2p / λ = w / v. Таким образом, закон распространения поперечного возмущения можно будет описать формулой: s = A * cos (w * t — k * x + φ). Это выражение называется уравнением плоской волны.
Величина в скобках — это волновая фаза в произвольной точке. Вычитаемое же k * x + φ является начальной фазой.
Фазовая скорость
Поперечная волна в плоскости описывается через s, то есть смещением от точки равновесия в любой точке пространства в произвольно выбранное время. Фактически это проекция вектора смещения на направление колебаний.
Если рассмотреть волну в зафиксированный момент времени, то формула примет вид: s (x, t) = A * cos (-2p * x / λ). Для исследования, как будет совершаться колебание, лучше всего построить график распространения возмущения. В декартовых системах координат по оси абсциссы нужно будет отложить смещение (s), а ординаты — точку X .
Схема изменения волны будет выглядеть следующим образом. В начальный момент времени упругое тело получит деформацию и смещение составит величину А. Затем по плавной линии интенсивность S будет спадать до тех пор, пока не поменяет знак. Через некоторое время ситуация повторится. Расстояние между двумя вершинами, а именно точками, колеблющимися в одной фазе, называют длиной волны. Можно сказать, что длина является пространственным периодом.
Смотря на формулу, можно утверждать, что с ростом t график будет смещаться влево. В этом случае интерес представляет не причина перемещения, а скорость. Для того чтобы фаза была постоянной, скобка в формуле должна быть константой. Из этого следует, что (2 * p / λ) * x = wt — const. Для упрощения выражения левую и правую часть можно умножить на λ и разделить на 2*p.
В результате получится: x = (λ * w / 2 * p) * t — (const * x / 2 * p). Для удобства первый член можно обозначить буквой C, а второй X 0. Если вспомнить утверждение, описывающее равномерное прямолинейное движение x (t) = x 0 + Vx * t, то можно обнаружить сходство с полученным выражением. Таким образом, можно сказать, что скорость перемещения волновой поверхности, то есть плоскости, в которой фаза во всех точках одна и та же, называется фазовой скоростью.
Исходя из сказанного, можно записать: x = x0 + c *t, где C = λ * w / 2 * p. Омега, делённая на два пи — это частота. Её принято обозначать буквой ν. Отсюда можно дать определение фазовой скорости: c является характеристикой колебания и представляет собой произведение длины волны на частоту. При этом длина λ характеризуется расстоянием, проходимым волной за время, равное одному периоду: λ = c * T.
Колебания в струне
Струной называется тонкая, гибкая, сильно натянутая нить с равномерно распределённой по длине плотностью. Согласно правилу, определяющему, какие волны называются поперечными, можно утверждать, что при колебании струна будет иметь максимум два отклонения. В начальный момент t0, пока воздействие на струну не оказывается, она не деформированная. Сила натяжения струны равняется F0. В определённое время к струне прикладывается дополнительная сила F. Если сложить эти две силы, то по струне побежит излом, направленный в противоположную сторону от вектора F общее.
За время ϴ положение струны изменится. Наблюдаемый излом пробежит расстояние, обозначаемое L. При этом конец струны переместится на расстояние Δ L. Для рассматриваемого случая фазовая скорость представляет излом, бегущий вдоль струны.
Физически распространение колебания происходит плавно. При приложении деформации сначала один участок деформируется, а затем последовательно и остальные. Если на струне зафиксировать точку, то можно будет обнаружить особенность её перемещения, заключающуюся в том, что после внешнего воздействия она начнёт перемещаться кверху. Так как струна прямая, то все частички движутся с одинаковой скоростью V.
Анализируя ситуацию, можно сказать, что фазовая скорость равняется расстоянию, пройденному изломом, делённому на время: c = L / ϴ. За то же самое время частицы струны поднимаются со скоростью V. Отсюда можно найти скорость движения струны: V = ΔL / ϴ. Получается, что на частицы действует сила, заставляющая их двигаться вверх с одной и той же скоростью. Для изменения импульса силы можно записать формулу, используя второй закон Ньютона: F * ϴ = Δp. При этом следует отметить, что импульсом будет обладать лишь та часть струны, которая уже изломалась.
Изменение импульса происходит за счёт вовлечения всё большей массы струны. Поэтому верно будет записать: Δp = m * V. Свойством этой массы является равномерное распределение по струне. Обозначается этот параметр греческой буквой ρ, называется линейной плотностью и находится из равенства: ρ = m / l. Приложенную силу можно определить из соотношения F / F0 = ΔL / L, отсюда F = F0 (ΔL / L).
Подставив формулы параметров в основное выражение и выполнив ряд преобразований, можно получить следующее выражение: c = √F0 / ρ. То есть скорость распространения поперечного колебания равняется корню квадратному из соотношения силы натяжения в струне к её погонной плотности.
Пример решения задачи
В разделе «Колебания и волны» общей физики учащимся предлагается научиться решать задачи на нахождение фазовой скорости. Для её вычисления нужно понимать, что она зависит от силы натяжения и плотности деформируемого вещества. Отсюда следует, что для увеличения скорости нужно приложить большую силу, а для уменьшения — увеличить плотность материала. Ярким примером этого является гитара, в которой шестая струна толще, чем первая.
Вот пример типовой задачи на нахождение фазового параметра. Пусть имеется верёвка с массой 0,85 кг. Её натянули между двумя опорами, находящимися на расстоянии 30 метров друг от друга. Сила натяжения верёвки составляет 1950 ньютон. Нужно вычислить, за какое время импульс перейдёт от одной из опор к другой. Решение примера необходимо выполнять в следующей последовательности:
Пожалуй, в классификации волн поперечные колебания являются одним из самых интересных видов возмущений. Их особенность в том, что возникают они только в твёрдых телах. Ведь в жидкой и газообразной среде физически невозможно появление противодействующих упругих сил. Решение задач предполагает знание формул смещения при распространении волны и фазовой скорости, а также закона, по которому описывается колебание.
При этом важно понимать, что частота возмущений волны совпадает с частотой источника, их вызвавшего. Это следует из того, что колебания частиц среды являются вынужденными, а значит, не зависят от свойств пространства, в котором они распространяются. Поэтому при переходе из одной среды в другую частота остаётся неизменной, а измениться могут лишь скорость и длина.
Предыдущая
ФизикаУдельный вес – формулы и примеры расчетов
Следующая
ФизикаФормула давления – примеры и условия расчетов
Источник
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механические волны, длина волны, звук.
Механические волны – это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).
Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.
Продольные и поперечные волны.
Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия. На рис. 1 показана продольная волна, представляющая собой колебания плоских слоёв среды; направление, вдоль которого колеблются слои, совпадает с направлением распространения волны (т. е. перпендикулярно слоям).
 |
| Рис. 1. Продольная волна |
Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого. На рис. 2 каждый слой колеблется вдоль самого себя, а волна идёт перпендикулярно слоям.
 |
| Рис. 2. Поперечная волна |
Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.
Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов*.
Важно отметить, что частицы среды при прохождении волны совершают колебания вблизи неизменных положений равновесия, т. е. в среднем остаются на своих местах. Волна, таким образом, осуществляет
перенос энергии, не сопровождающийся переносом вещества.
Наиболее просты для изучения гармонические волны. Они вызываются внешним воздействием на среду, меняющимся по гармоническому закону. При распространении гармонической волны частицы среды совершают гармонические колебания с частотой, равной частоте внешнего воздействия. Гармоническими волнами мы в дальнейшем и ограничимся.
Рассмотрим процесс распространения волны более подробно. Допустим, что некоторая частица среды (частица ) начала совершать колебания с периодом . Действуя на соседнюю частицу она потянет её за собой. Частица в свою очередь, потянет за собой частицу и т. д. Так возникнет волна, в которой все частицы будут совершать колебания с периодом .
Однако частицы имеют массу, т. е. обладают инертностью. На изменение их скорости требуется некоторое время. Следовательно, частица в своём движении будет несколько отставать от частицы , частица будет отставать от частицы и т. д. Когда частица пустя время завершит первое колебание и начнёт второе, своё первое колебание начнёт частица , находящаяся от частицы на некотором расстоянии .
Итак, за время, равное периоду колебаний частиц, возмущение среды распространяется на расстояние . Это расстояние называется длиной волны. Колебания частицы будут идентичны колебаниям частицы колебания следующей частицы будут идентичны колебаниям частицы и т. д. Колебания как бы воспроизводят себя на расстоянии можно назвать пространственным периодом колебаний; наряду с временным периодом она является важнейшей характеристикой волнового процесса. В продольной волне длина волны равна расстоянию между соседними сжатиями или разрежениями (рис. 1). В поперечной – расстоянию между соседними горбами или впадинами (рис. 2). Вообще, длина волны равна расстоянию (вдоль направления распространения волны) между двумя ближайшими частицами среды, колеблющимися одинаково (т. е. с разностью фаз, равной ).
Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:
.
Частотой волны называется частота колебаний частиц:
.
Отсюда получаем связь скорости волны, длины волны и частоты:
. (1)
| На поверхности жидкости могут существовать волны особого типа, похожие на поперечные – так называемые поверхностные волны. Они возникают под действием силы тяжести и силы поверхностного натяжения. |
Звук.
Звуковыми волнами в широком смысле называются всякие волны, распространяющиеся в упругой среде. В узком смысле звуком называют звуковые волны в диапазоне частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом. Ниже этого диапазона лежит область инфразвука, выше – область ультразвука.
К основным характеристикам звука относятся громкость и высота.
Громкость звука определяется амплитудой колебаний давления в звуковой волне и измеряется в специальных единицах –децибелах (дБ). Так, громкость 0 дБ является порогом слышимости, 10 дБ – тиканье часов, 50 дБ – обычный разговор, 80 дБ – крик, 130 дБ – верхняя граница слышимости (так называемый болевой порог).
Тон – это звук, который издаёт тело, совершающее гармонические колебания (например, камертон или струна). Высота тона определяется частотой этих колебаний: чем выше частота, тем выше нам кажется звук. Так, натягивая струну, мы увеличиваем частоту её колебаний и, соответственно, высоту звука.
Скорость звука в разных средах различна: чем более упругой является среда, тем быстрее в ней распространяется звук. В жидкостях скорость звука больше, чем в газах, а в твёрдых телах – больше, чем в жидкостях.
Например, скорость звука в воздухе при равна примерно 340 м/с (её удобно запомнить как “треть километра в секунду”)*. В воде звук распространяется со скоростью около 1500 м/с, а в стали – около 5000 м/с.
Заметим, что частота звука от данного источника во всех средах одна и та же: частицы среды совершают вынужденные колебания с частотой источника звука. Согласно формуле (1) заключаем тогда, что при переходе из одной среды в другую наряду со скоростью звука изменяется длина звуковой волны.
| Если хочешь найти расстояние до грозовых туч в километрах, посчитай, через сколько секунд после молнии придёт гром, и раздели полученное число на три. |
Источник
