Какие свойства сложение ответ


Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
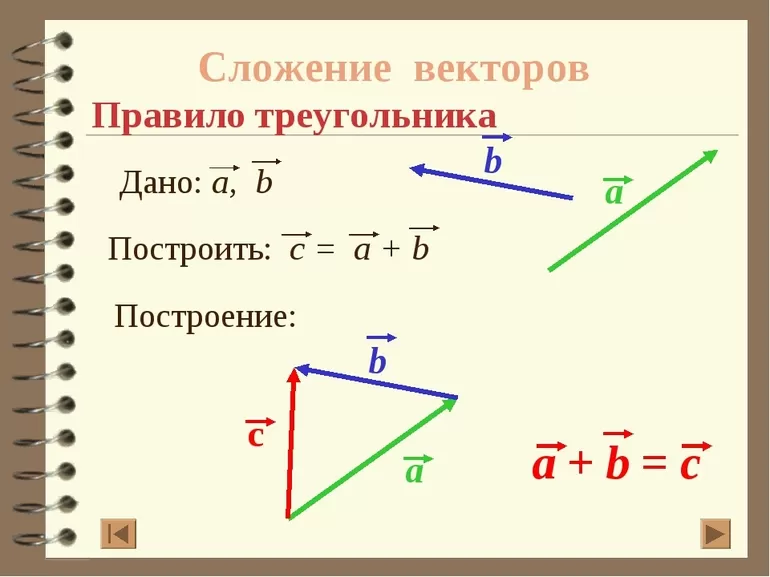
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
Сложение натуральных чисел.
Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
Сумма — это сложение чисел. Знак плюс “+”.
В буквенном виде этот пример будет выглядеть так:
a+b=c
Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.
Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:
4+3=3+4
Называется такое свойство слагаемых переместительным законом сложения.
Переместительный закон сложения.
От перемены мест слагаемых сумма не меняется.
В буквенной записи переместительный закон выглядит так:
a+b=b+a
Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:
(1+2)+4=7
Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:
1+(2+4)=7
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:
(1+2)+4=1+(2+4)
Это свойство сложения называется сочетательным законом сложения.
Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a+b)+c=a+(b+c)
Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30
Свойство сложения с нулем.
При сложении числа с нулем, в результате сумма будет тем же самым числом.
3+0=3
0+3=3
3+0=0+3
В буквенном выражение сложение с нулем будет выглядеть так:
a+0=a
0+a=a
Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:
 Второй вариант таблицы сложения.
Второй вариант таблицы сложения.
 Если посмотрим на таблицы сложения, видно как работает переместительный закон.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.
В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.
В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.
Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.
Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a
Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22
Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.
Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921
Источник
Технологическая карта урока математики во 2 классе
Учитель: Рябова Н.М.
урок открытия нового знания
Технология построения урока
проблемно-диалогическая, системно – деятельностный подход в обучении
Тема
Свойства сложения
Цель
Познакомить с переместительным и сочетательным свойствами сложения, научить применять их при нахождении значений числовых выражений, записывать изученные свойства, используя буквенные обозначения.
Основные термины, понятия
Слагаемое, сумма, сложение, переместительное свойство, сочетательное свойство, свойство сложения с нулем
Предметные умения
– иметь представление о понятиях “переместительное свойство”, “сочетательное свойство”;
– уметь использовать изученные свойства при вычислениях;
– уметь записывать изученные законы и свойства, используя буквенные обозначения;
ЛичностныеУУД:
– устанавливать связь между целью учебной деятельности и ее мотивом;
– определять общие для всех правила поведения ;
– определять правила работы в паре;
– оценивать усваиваемое содержание (исходя личностных ценностей);
– устанавливать связь между целью деятельности и ее результатом; -формировать личностные качества: любознательность, трудолюбие, целеустремлённость и настойчивость в достижении цели; – обосновывать свою позицию, высказывать свое мнение; – проявлять самостоятельность, личную ответственность.
Метапредметные критерии сформированности УУД:
Регулятивные УУД:
– определять и формулировать цель деятельности на уроке;
– высказывать свое предположение на основе учебного материала;
– отличать верно выполненное задание от неверного;
– осуществлять самоконтроль;
– совместно с учителем и одноклассниками давать оценку деятельности на уроке.
Познавательные УУД:
– ориентироваться в учебнике, тетради;
– ориентироваться в своей системе знаний (определять границы знания/незнания);
– проводить анализ учебного материала;
– проводить классификацию, указывая на основание классификации;
Коммуникативные УУД:
– слушать и понимать речь других;
– уметь с достаточной полнотой и точностью выражать свои мысли ;
-владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Фронтальная
Работа в парах
Индивидуальная
Книгопечатная продукция
М.И.Моро. Математика. 2 класс. Часть 1.
Технические средства обучения
Компьютер
Медиапроектор
Технология изучения
I. Мотивация
к учебной деятельности
Цель:
– создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность;
Эмоциональный настрой на урок.
-Долгожданный дан звонок.
Начинается урок.
-Улыбнулись друг другу-(слайд)
Давайте приступим к работе .
И пусть интересным будет урок.
А девиз нашего урока: «Будьте внимательны и у вас все получится» (слайд)
Нас на уроке ждут великие дела.(слайд)
Проговаривание правил сотрудничества
Определять и проявлять правила поведения при сотрудничестве.
(Л /УУД).
Правильно формулировать собственное мнение.
(Р/УУД).
II. Актуализация знаний
Цель:
– обеспечение готовности учащихся к включению в продуктивную обучающую деятельность, повторение изученного материала, необходимого для «открытия нового знания».
Организация живого диалога
– Какое сейчас время года ? (осень). -Кто любит осень?
-Какое сегодня число? (19)
– Что вы можете сказать о числе 19?
( двузначное, состоит из 1 дес. и 9 ед.).
-Почему число 19-двузначное? (в его записи использовано 2 цифры).
-Представьте число 19 в виде суммы разрядных слагаемых. (19=10+9)
– распределите числа на 2группы(слайд)
4, 27, 83, 9, 16, 5, 72, 31, 94.
-по какому признаку вы это сделали?
-Какие числа мы называем однозначными?
-Почему числа называем двузначными?
– Укажите состав чисел.
-Прочитайте числа в порядке возрастания, (убывания).
-Прочитайте правильно числовые выражения и найдите их значения:
60+8=, 68-60=, 68-8= 30+(5+2)=, 90-(6+4). (слайд) -Правило: Действия, записанные в скобках, выполняются первыми. -Найдите периметр треугольника со сторонами 4см, 5см, 6см – Что такое периметр?(слайд)
–Периметр-это сумма длин сторон многоугольника.
Ведение живого диалога: свободно говорят, высказывают свою точку зрения
Выделение и осознание того, что уже пройдено (Р/УУД).
Смыслообразовани (Л/УУД).
Слушать и понимать речь других (К /УУД)
III. Постановка целей, задач урока, мотивационная деятельность учащихся.
Цель:
– обсуждение затруднений, проговаривание цели урока, темы.
– Прочитайте слова: слагаемое, уменьшаемое, разность, слагаемое, вычитаемое, сумма. (слайд)
– Кто мне поможет разделить эти слова на группы? (I – компоненты действия сложения, II – компоненты действия вычитания) (слайд)
– Назовите их.(Компоненты при сложении называются: слагаемое, слагаемое, сумма.
Компоненты при вычитании называются: уменьшаемое, вычитаемое, разность)
-Как вы думаете, к какой группе можно отнести слово «свойство…» ? (к I группе)
– Кто догадался, какая у нас сегодня тема урока? (свойства сложения) (слайд)
– Чему мы будем учиться на уроке?
(познакомимся со свойствами сложения и будем их применять при нахождении значений числовых выражений).
-С каким свойством сложения вы уже знакомы? ( с переместительным)
-сравни: 30+8*8+30, 7+10*10+7 (слайд)
– Как читается переместительный закон сложения? (От перестановки слагаемых сумма не изменяется)
-Не вычисляя, составьте верные числовые равенства. ( 50 + 8 = * + 50,
5 + 40 = 40 + * (слайд)
* + 8= 8 + 2)
– Зачем нужно знать это свойство при вычислениях? ( Легче к большему числу прибавить меньшее).
Запись с помощью букв: а+в=в+а (слайд)
-Работа по учебнику с.44, №1. (взаимопроверка)
– А найдите значение этого числового выражения:
6 + 7 + 8 + 9 + 3 + 4 + 1 + 2 = (слайд)
-У кого это задание вызвало затруднение?
-Проблема. ( Не достаточно знаний, чтобы легко и быстро справиться с заданием.)
Вспоминают названия компонентов при сложении.
Анализируют слова, деля их на группы.
Формулируют цель урока.
Определять и формулировать цель деятельности на уроке (Р/УУД).
Высказывать свое предположение на основе учебного материала (Р/УУД).
Проводить классификацию, указывая на основание классификации (П /УУД)
Ориентироваться в своей системе знаний (определять границы знания/незнания) (П /УУД)
Уметь с достаточной полнотой и точностью выражать свои мысли (К /УУД)
IV. Первичное усвоение новых знаний
Цель:
– обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы. Организация исследовательской деятельности, выведение алгоритма.
– Давайте вместе добудем эти знания!
(рассмотреть с помощью кружков разного цвета еще одно свойство сложения) (слайд)
(5+3)+2=5+(3+2)
10 = 10
Вывод: Результат сложения не изменится, если два соседних слагаемых заменить их суммой. Это сочетательный закон сложения. (на доске).
– (а+в)+с=а+(в+с)
– Эти два закона работать могут вместе.
Давайте вернемся к нашему числовому выражению и решим его.
– Какие у вас будут предложения?
(Можно применить переместительное свойство сложения, а затем сочетательное свойство сложения).
(6+4)+(7+3)+(8+2)+(9+1)=40 (слайд)
Вывод: Используя оба свойства сложения, можно складывать числа в любом порядке.
-С какими свойствами сложения мы с вами познакомились? (ответы детей)
Решают проблему, обсуждая и выдвигая гипотезы в совместной деятельности, сравнивают, анализируют, осуществляют поиск необходимой информации
Выполняют задание, проговаривая свойства сложения.
Составляют буквенную запись свойств сложения.
Работают с учебником в парах. Выполняют задания
Проводить анализ учебного материала (П /УУД)
Ориентироваться в учебнике, тетради (П /УУД)
Определять правила работы в паре (Л /УУД)
Слушать и понимать речь других (К /УУД)
Отличать верно выполненное задание от неверного (Р/УУД).
V.Первичное закрепление
Цель:
– обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации. Выполнение заданий с проговаривание в громкой речи. Запись с помощью буквенных выражений.
(Работа в паре) Дополните формулировку свойств пропущенными словами.
От _________ слагаемых сумма ___________.
Результат _______________не изменится, если соседние _____________заменить их суммой.
Чтобы к сумме двух чисел прибавить ___________, можно к первому числу прибавить сумму __________ и третьего числа.
Игра «Помоги героям вспомнить свойства»
– В каком из примеров использовано сочетательное свойство? (переместительное)
3 + (2 + 1) = (3 + 2) + 1
21 – 17 = 17 – 21
15 + 18 = 18 + 15
4 + 9 = 13
46 + 0 = 46
– А для чего нам нужно знать свойства сложения? (для быстрого, рационального вычисления выражений) —
Работа по учебнику: с.44, правило. с.45, № 3. (устно)
Найти значения числовых выражений:
( с проговариванием в громкой речи )
6+9+4+1=
17+8+3+2=
Участвуют в диалоге.
Выполняют задания в парах, ведут обсуждение, учатся принимать на себя ответственность за результат учебного труда.
Определять правила работы в паре (Л /УУД)
Владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка. (К /УУД)
VI. Самостоятельная работа с самопроверкой.
Цель:
– умение применять правило в самостоятельной деятельности.
– Самостоятельно найдите рациональный способ вычисления суммы, пользуясь свойствами сложения.
-Какими свойствами вы будете пользоваться?
1)Работа по карточке(дифференцированные задания).
Карточка №1 15+6+7+5+4+3= 40+7+20+3= 82+6+8+4= 26+13+4+7 Карточка №2 7+9+5+1+3+5= 50+6+40+4= 32+7+8+3= Карточка № 3 7+8+3+2= 15+9+5+1=
САМОПРОВЕРКА. (слайд) №1. 40,70,100,50 №2. 30,100,50. №3. 20,30. –Кто выполнил без ошибок? -Кто допустил ошибки?
2)Найдите значения числовых выражений (на время): (слайд)
7+9+3+1=(7+3)+(9+1)=20
15 + 8 + 2= 15 + (8 + 2) = 25
1 + 39 + 20 = (1 + 39) + 20 = 60
63 + 14 + 6 = 63 + (14 + 6) = 83
12 + 8 + 10 = (12 + 8) + 10 = 30
6+5+4=(6+4)+5=15
ПРОВЕРКА: САМОПРОВЕРКА.
– Кто допустил ошибки при вычислении?
– У кого ошибок нет?
– Оцените свою работу.(смайлик на полях)
2) Применение нового знания при решении задач.
1)Построить ломаную из трех звеньев: 6см, 2см, 4см.Найти ее длину?
2)Учебник.С.45, № 5. Задача.
( Решение: 30+30+20+20=
(30+20)+(30+20)=100(мм)-периметр четырехугольника.
100мм=10см
Ответ:10см .
Самостоятельное решение в тетради.
Осуществляют самоконтроль и самооценку своей работы.
Отличать верно выполненное задание от неверного (Р/УУД).
Осуществлять самоконтроль (Р/УУД).
Оценивать усваиваемое содержание (Л /УУД)
VII. Подведение итогов учебного занятия. Рефлексия деятельности
Цель:
– анализ и оценка успешности достижения цели; выявление качества и уровня овладения знаниями.
ВОПРОСЫ:
-Ребята, какова была тема урока?
-Какую цель вы ставили перед собой?
-Достигли ли поставленной цели?
– В чём ценность нового знания?
-Оцените свою работу на уроке.(смайлики)
Весело звенит звонок.
Вот и закончился наш урок.
Благодарю за внимание.
Осознание результатов своей учебной деятельности;
Самооценка результатов своей работы и работы всего класса.
Устанавливать связь между целью деятельности и ее результатом (Л /УУД)
Совместно с учителем и одноклассниками давать оценку деятельности на уроке (Р/УУД).
VIII Домашнеезадание.
Комментировать.
С. 44,правило, с.45, № 4, с. 46, №1.-применить изученные свойства сложения при нахождении значения числовых выражений.
Резерв урока.
Найти значение числовых выражений: 30+40+7 = 30+4+6= 20+70+2= 40+6+3 60+30+8= 60+5+4=
Сравни: 2дм1см*12см 38мин.*1ч.
Реши задачу и составь обратные:
В гараже было 11машин. Утром 6 машин уехало. Сколько машин осталось в гараже?
Источник
