Какие свойства сложения были использованы

- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Как в равенстве а + b = с называют число а? Число b? Число с? Выражение а + b?
- a — слагаемое
- b — слагаемое
- c — сумма
- a+b — сумма
2. Сформулируйте переместительное свойство сложения.
От перестановки слагаемых сумма не меняется.
3. Как записывают в буквенном виде переместительное свойство сложения?
а + b = b + а
4. Сформулируйте сочетательное свойство сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.
5. Как записывают в буквенном виде сочетательное свойство сложения?
(a + b) + c = a + (b + c)
6. Каким свойством обладает число 0 при сложении?
Если одно из двух слагаемых равно 0, то сумма равна другому слагаемому.
Решаем устно
1. Вычислите:
- 23 + 17 = 40
- 230 + 17 = 247
- 23 + 170 = 193
- 30 — 13 = 17
- 300 — 130 = 170
- 300 — 13 = 287
- 12 • 4 = 48
- 12 • 40 = 480
- 120 • 40 = 4800
- 72 : 8 = 9
- 720 : 8 = 90
- 720 : 80 = 9
2. Назовите два последовательных натуральных числа, сумма которых равна 91.
Любые два последовательных натуральных числа различаются между собой на 1.
1) 90 — 1 = 90 — сумма искомых натуральных чисел без различающих их 1.
2) 90 : 2 = 45 — наименьшее из искомых натуральных чисел.
3) 45 + 1 = 46 — наибольшее из искомых натуральных чисел.
Ответ: 45 и 46.
3. Назовите двузначное число, сумма цифр которого равна наибольшему однозначному числу. Сколько существует таких чисел?
Наибольшее двузначное число — 9.
Значит условию удовлетворяют следующие двузначные числа: 18, 81, 27, 72, 36, 63, 45, 54, 90. Значит существует 9 таких чисел.
Упражнения
167. Найдите сумму:

168. Выполните сложение:

169. Аня и Коля решали задачи. Коля решил 26 задач, а Аня — на 16 задач больше. Сколько задач решили Коля и Аня вместе?

1) 26 + 16 = 42 (задачи) — решила Аня.
2) 42 + 26 = 68 (задач) — решили Коля и Аня вместе.
Ответ: 68 задач.
170. Миша купил книгу за 170 р., что на 12 р. меньше, чем заплатил Петя за свою новую книгу. Сколько рублей заплатили за книги Миша и Петя вместе?

1) 170 + 12 = 182 (рубля) — заплатил за книгу Петя.
2) 170 + 182 = 352 (рубля) — заплатили за свои книги Петя и Миша вместе.
Ответ: 352 рубля.
171. Выполните сложение, выбирая удобный порядок вычислений:
- (42 + 37) + 58 = (42 + 58) + 37 = 100 + 37 = 137
- 29 + (98 + 71) = (29 + 71) + 98 = 100 + 98 = 198
- (215 + 818) + 785 = (215 + 785) + 818 = 1 000 + 818 = 1 818
- 634 + (458 + 166) = (634 + 166) + 458 = 800 + 458 = 1 258
- 183 + 732 + 268 + 317 = (183 + 317) + (732 + 268) = 500 + 1 000 = 1 500
- 339 + 584 + 416 + 661 = (339 + 661) + (584 + 416) = 1 000 + 1 000 = 2 000
- (15 083 + 1 458) + (4 917 + 6 542) = (15 083 + 4 917) + (1 458 + 6 542) = 20 000+ 8 000 = 28 000
- (1 654 + 18 135) + (7 346 + 11 865) = (1 654 + 7 346) + (18 135 + 11 865) = 9 000 + 30 000 = 39 000
172. Используйте свойства сложения при вычислении суммы:
- (146 + 322) + 178 (322 + 178) + 146 = 500 + 146 = 646
- 784 + (179 + 116) = (784 + 116) + 179 = 900 + 179 = 1 079
- 625 + 481 + 75 + 219 = (625 + 75) + (481 + 219) = 700 + 700 = 1 400
- 427 + 88 + 273 + 112 = (427 + 273) + (88 + 112) = 700 + 200 = 900
173. Стена Московского Кремля состоит из трёх участков: южного, восточного и западного. Длина южного участка составляет 685 м, что на 45 м меньше длины восточного. Длина западного участка на 135 м больше длины южного. Сколько метров составляет общая длина стен Московского Кремля?

1) 685 + 45 = 730 (метров) — длина восточной стены Кремля.
2) 685 + 135 = 820 (метров) — длина Западной стены Кремля.
3) 685 + 730 + 820 = 2 235 (метров) — общая длина стен Кремля.
Ответ: 2 235 метров.
174. У Иры в коллекции есть 26 марок, посвящённых историческим событиям, а также марки, посвящённые архитектуре и спорту. Марок по архитектуре у неё на 15 больше, чем по истории, и на 14 меньше, чем на спортивную тему. Сколько марок в коллекции у Иры?

1) 26 + 15 = 41 (марки) — по архитектуре.
2) 41 + 14 = 55 (марок) — посвящённых спорту.
3) 26 + 41 + 55 = 122 (марки) — всего в коллекции Иры.
Ответ: 122 марки.
175. На одной полке было 17 книг, на второй — на 18 книг больше, чем на первой, а на третьей — на 6 книг больше, чем на первой и второй вместе. Сколько всего книг было на трёх полках?

1) 17 + 18 = 35 (книг) — на второй полке.
2) 35 + 17 = 52 (книги) — на первой и второй полке вместе.
3) 52 + 6 = 58 (книг) — на третьей полке.
4) 52 + 58 = 110 (книг) всего на трёх полках.
Ответ: 110 книг.
176. Отправившись в велосипедный поход, группа туристов в первый день проехала 42 км, что на 12 км меньше, чем во второй, а в третий — на 4 км больше, чем в первый и второй вместе. Сколько километров проехали туристы за три дня?

1) 42 + 12 = 54 (км) — туристы проехали во второй день.
2) 42 + 54 = 96 (км) — туристы проехали всего за первый и второй день.
3) 96 + 4 = 100 (км) — туристы проехали в третий день.
4) 96 + 100 = 196 (км) — туристы проехали за три дня всего.
Ответ: 196 км.
177. Упростите выражение:
- (74 + x) + 38 = (74 + 38) + x = 112 + x
- 238 + (а + 416) = (238 + 416) + a = 654 + a
- у + 324 + 546 = y + (325 + 546) = y + 870
- 2 753 + m + 4 199 = (2 753 + 4 199) + m = 6 952 + m
- (b + 457) + (143 + 872) = b + (457 + 143) + 872 = b + 600 + 872 = b + 1 472
- (2 235 + с) + (4 671 + 1 765) = (2 235 + 1 765) + c + 4 671 = (4 000 + 4 671) + c = 8 671 + c
- (1 696 + 3 593) + (р + 1 304) = (1 696 + 1 304) + 3 593 + p = (3 000 + 3 593) + p = 6 593 + p
- (5 432 + 8 951) + (4 568 + а + 1 049) = (5 432 + 4 568) + (8 951 + 1 049) + a = (10 000 + 10 000) + a = 20 000 + a
178. Упростите выражение:
- (56 + а) + 14 = (56 + 14) + a = 70 + a
- 342 + (b + 58) = (342 + 58) + b = 400 + b
- 805 + х + 195 = (805 + 195) + x = 1 000 + x
- m + 4 563 + 1 837 = m + (4 563 + 1 837) = m + 6 400
179. Дядя Фёдор выехал из города в Простоквашино в 15 ч 40 мин и потратил на дорогу 3 ч 50 мин. В котором часу дядя Фёдор приехал в Простоквашино?
1) 15 ч 40 мин + 3 ч 50 мин = (15 ч + 3 ч) + (40 мин + 50 мин) = 18 ч + 90 мин = 18 ч + (60 мин + 30 мин) = (18 ч + 1 ч) + 30 мин = 19 ч 30 мин
Ответ: дядя Фёдор приехал в Простоквашино в 19 часов 30 минут.
180. Поезд отправляется от станции А в 9 ч 57 мин и прибывает на станцию В через 2 ч 36 мин. В котором часу поезд прибывает на станцию В?
1) 9 ч 57 мин + 2 ч 36 мин = (9 ч + 2 ч) + ( 57 мин + 36 мин) = 11 ч + 93 мин = 11 ч + (60 мин + 33 мин) = (11 ч + 1 ч) + 33 мин = 12 ч 33 мин
Ответ: поезд прибывает на станцию В в 12 часов 33 минуты.
181. Найди:
- Как изменится сумма, если одно из слагаемых увеличить на 12? Сумма увеличится на 12.
- Как изменится сумма, если одно из слагаемых увеличить на 23, а второе — на 17? Сумма увеличится на 40 (23 + 17 = 40).
- Как изменится сумма, если одно из слагаемых уменьшить на 34? Сумма уменьшится на 34.
- Как изменится сумма, если одно из слагаемых уменьшить на 16, а второе — на 9? Сумма уменьшится на 25 (16 + 9 = 25).
- Как изменится сумма, если одно из слагаемых увеличить на 28, а второе уменьшить на 15? Сумма увеличится на 13 (28 — 15 = 13).
- Одно из слагаемых увеличили на 3. На сколько надо увеличить второе слагаемое, чтобы сумма увеличилась на 14? Второе слагаемое надо увеличить на 11 (14 — 3 = 11).
- Одно из слагаемых увеличили на 8. Как надо изменить второе слагаемое, чтобы сумма:
- а) увеличилась на 3 — Надо второе слагаемое уменьшить на 5 (8 — 5 = 3).
- б) уменьшилась на 5 — Надо второе слагаемое уменьшить на 13 (13 — 8 = 5).
182. Найдите сумму:
- 76 м 39 см + 41 м 58 см = (76 м + 41 м) + (39 см + 58 см) = 117 м + 97 см = 117 м 97 см
- 4 км 238 м + 3 км 474 м = (4 км + 3 км) + (238 м + 474 м) = 7 км + 712 м = 7 км 712 м
- 64 м 86 см + 27 м 45 см = (64 м + 27 м) + (86 см + 45 см) = 91 м + 131 см = 91 м + (100 см + 31 см) = (91 м + 1 м) + 31 см = 92 м 31 см
- 16 км 527 м + 37 км 783 м = (16 км + 37 км) + (6 527 м + 783 м) = 53 км + 1 310 м = 53 км + (1 000 м + 310 м) = (53 км + 1 км) + 310 м = 54 км 310 м
- 12 ч 24 мин + 9 ч 18 мин = (12 ч + 9 ч) + (24 мин + 18 мин) = 21 ч + 42 мин = 21 ч 42 мин
- 35 мин 17 с + 16 мин 35 с = (35 мин + 16 мин) + (17 с + 35 с) = 51 мин + 52 с = 51 мин 52 с
- 18 ч 42 мин + 14 ч 29 мин = (18 ч + 14 ч) + (42 мин + 29 мин) = 32 ч + 71 мин = 32 ч + (60 мин + 11 мин) = (32 ч + 1 ч) + 11 мин = 33 ч 11 мин
- 53 мин 32 с + 44 мин 56 с = (53 мин + 44 мин) + (32 с + 56 с) = 97 мин + 88 с = (60 мин + 37 мин) + (60 с + 28 с) = 1 ч + (37 мин + 1 мин) + 28 с = 1 ч 38 мин 28 с
183. Найдите сумму:
- 4 дм 6 см + 5 дм 8 см = (4 дм + 5 дм) + (6 см + 8 см) = 9 дм + 14 см = 9 дм + (10 см + 4 см) = (9 дм + 1 дм) + 4 см = 10 дм 4 см
- 8 м 5 см + 6 м 96 см = (8 м + 6 м) + (5 см + 96 см) = 14 м + 101 см = 14 м + (100 см + 1 см) = (14 м + 1 м) + 1 см = 15 м 1 см
- 12 км 29 м + 24 км 92 м = (12 км + 24 км) + (29 м + 92 м) = 36 км 121 м
- 2 т 4 ц 56 кг + 9 т 6 ц 48 кг = (2 т + 9 т) + (4 ц + 6 ц) + (56 кг + 48 кг) = 11 т + 10 ц +104 кг = (11 т + 1 т) + (100 кг + 4 кг) = 12 т + 1 ц + 4 кг = 12 т 1 ц 4 кг
- 3 ч 48 мин + 2 ч 26 мин = (3 ч + 2 ч) + (48 мин + 26 мин) = 5 ч + 74 мин = 5 ч + (60 мин + 14 мин) = (5 ч + 1 ч) + 14 мин = 6 ч 14 мин
- 25 мин 17 с + 7 мин 54 с = (25 мин + 7 мин) + (17 с + 54 с) =32 мин + 71 с = 32 мин + (60 с + 11 с) = (32 мин + 1 мин) + 11 с = 33 мин + 11 с
184. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

185. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

186. Не выполняя вычислений, расположите данные суммы в порядке возрастания:
- 129 + 288
- 288 + 659
- 782 + 659
- 782 + 943
- 943 + 1 105
- 1 105 + 2 563
187. Найдите сумму наиболее удобным способом:
1) 1 + 2 + 3 + … + 9 + 10
1 + 2 + 3 + … + 9 + 10 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 + 10 = 10 + 10 + 10 + 10 + 5 + 10 = 10 • 4 + 5 + 10 = 40 + 5 + 10 = 55
Комментарий: В данном примере надо сложить 11 чисел. из них:
- есть один десяток
- четыре пары образуют десяток
- число 5
В результате получаем 5 десятков плюс 5, то есть число 55.
2) 1 + 2 + 3 + … + 99 + 100
1 + 2 + 3 + … + 99 + 100 = (1 + 99) + (2 + 98) + (3 + 97) + … + (49 + 51) + 50 + 100 = 100 • 49 + 50 + 100 = 4900 + 50 + 100 = 5 500.
188. Найди:
1) На сколько сумма 1 + 3 + 5 + … + 99 меньше, чем сумма 2 + 4 + 6 + … + 100?
1) 1 + 3 + 5 + … + 99 = (1 + 99) + (3 + 97) + (5 + 95) + … + (49 + 51) = 100 • 25 = 2 500 — слагаемыми являются только нечётные числа, а от 1 до 49 их 25 штук.
2) 2 + 4 + 6 + … + 100 = (2 + 98) + (4 + 96) + (6 + 94) + … + (48 + 52) + 50 + 100 = 100 • 24 + 50 + 100 = 2 400 + 50 + 100 = 2 550 — слагаемыми являются только нечётные числа, а их 24 пары по 100 плюс число 50 плюс число 100.
3) 2 550 — 2 500 = 50
Ответ: на 50.
2) Какая из сумм 1 + 3 + 5 + … + 2 001 и 2 + 4 + 6 + … + 2 000 больше и на сколько?
1) 1 + 3 + 5 + … + 2 001 = (1 + 1 999) + (3 + 1997) + (5 + 1995) + … + (999 + 1 001) + 2 001 = 2 000 • 500 + 2 001 = 1 000 000 + 2 001 = 1 002 001
2) 2 + 4+ 6 + … + 2 000 = (2 + 1998) + (4 + 1996) + (6 + 1994) + … + (998 + 1 002) + 1 000 + 2 000 = 2 000 • 490 + 1 000 + 2 000 = 2 000 + 500 + 1 000 = 1 000 000 + 1 000 = 1 001 000
3) 1 002 001 — 1 001 000 = 1 001
Ответ: сумма 1 + 3 + 5 + … + 2 001 больше суммы 2 + 4 + 6 + … + 2 000 на 1 001.
189. В записи 4 4 4 4 4 4 4 4 поставьте между некоторыми цифрами знак «+» так, чтобы получилось выражение, значение которого равно 500.
444 + 44 + 4 + 4 + 4 = (444 + 44) + (4 + 4 + 4) = 488 + 12 = 500
Ответ: 444 + 44 + 4 + 4 + 4
190. Замените звёздочки числами так, чтобы сумма любых трёх соседних чисел была равна 20: 7, *, *, *, *, *, *, 9.
7, 9 , 4, 7, 9, 4, 7, 9
7 + 9 + 5 = 20; 9 + 4 + 7 = 20; 4 + 7 + 9 = 20 и т.д.
Ответ: 7, 9 , 4, 7, 9, 4, 7, 9.
191. Слава разрезал проволоку на кусочки и составил фигуру, изображённую на рисунке 65. Мог ли Слава разрезать эту же проволоку так, чтобы составить фигуру, изображённую на рисунке 66?
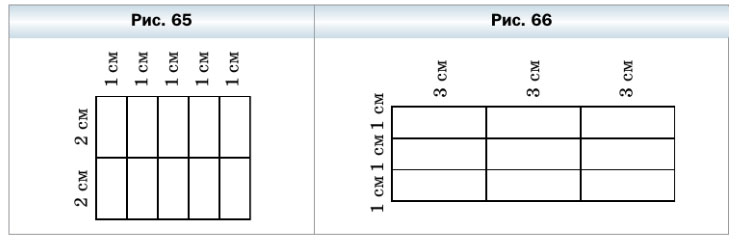
Посчитаем, сколько проволоки Слава потратил на составление первой фигуры:
- 15 кусочков по 1 см
- 12 кусочков по 2 см
1) 15 • 1 + 12 • 2 = 15 + 24 = 39 (см) — проволоки использовано на первую фигуру.
Посчитаем, сколько проволоки Славе потребуется для составления второй фигуры:
- 12 кусочков по 3 см
- 12 кусочков по 1 см
2) 12 • 3 + 12 • 1 = 36 + 12 = 48 (см) — проволоки потребуется для второй фигуры.
3) 39 < 48, значит проволоки с первой фигуры не хватит для изготовления второй фигуры.
Ответ: нет, длины проволоки, использованной для первой фигуры, не хватит для изготовления второй фигуры.
Упражнения для повторения
192. Отметьте на координатном луче натуральные числа, которые больше 6, но меньше 12.

193. Запишите все шестизначные числа, которые больше 999 888 и оканчиваются цифрой 5.
- 999 895
- 999 905
- 999 915
- 999 925
- 999 935
- 999 945
- 999 955
- 999 965
- 999 975
- 999 985
- 999 995
194. Скороход прошёл 24 км за 4 ч. На обратном пути он увеличил скорость на 2 км/ч. Сколько времени он потратил на обратный путь?

1) 24 : 4 = 6 (км/ч) — скорость движения скорохода по пути туда.
2) 6 + 2 = 8 (км/ч) — скорость движения скорохода по пути обратно.
3) 24 : 8 = 3 (часа) — скороход потратил на обратный путь.
Ответ: 3 часа.
195. Вася старше своей сестры Светы на 5 лет. На сколько лет он будет старше Светы через 7 лет?
И через 7 лет, и через 10, и через любое количество лет разница в возрасте между Васей и Светой останется одинаковой — 5 лет. Это происходит потому, что с количество лет прибавляется с каждым годом для всех с одинаковой скоростью.
Ответ: Вася будет старше своей сестры Светы на 5 лет.
Задача от мудрой совы
196. Можно ли таблицу из пяти строк и шести столбцов заполнить натуральными числами так, чтобы сумма чисел каждой строки была равна 30, а сумма чисел каждого столбца — 20?

Мы знаем, что строк в таблице должно быть 5 и сумма натуральных чисел в каждой строке должна равняться 30. Значит сумма натуральных числе во всех пяти строках таблицы должна равняться:
1) 30 • 5 = 150
Мы знаем, что столбцов с таблице должно быть 6 и сумма всех натуральных чисел в каждом столбце таблицы должна равняться 20. Значит сумма натуральных числе во всех шести столбцах таблицы должна равняться:
2) 20 • 6 = 120
Получается, что сумма натуральных чисел в таблице, если считать по строкам и если считать по столбцам, не совпадает:
3) 150 ≠ 120
Значит таблицу с указанными условиями невозможно заполнить натуральными числами.
Ответ: нет, такую таблицу заполнить невозможно.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Источник
Тема: Свойства сложения.
Цель: познакомить со свойством сложения, основанным на группировке слагаемых.
– стремятся развивать внимание, память, логическое мышление, навыки сотрудничества со сверстниками и со взрослыми;
– проявляют самостоятельность.
– иметь представление о понятиях “переместительное свойство”, “сочетательное свойство”;
– уметь решать задачи изученных видов.
– прогнозируют результат деятельности, контролируют и оценивают, собственную деятельность и деятельность партнеров образовательному процессу, при необходимости вносят корректировки.
– аргументируют свою точку зрения, при возникновении спорных ситуаций не создают конфликтов.
Методы и формы обучения : частично- поисковый; индивидуальная, фронтальная, групповая.
Образовательные ресурсы: Книгопечатная продукция : М.И. Моро Математика. 2 класс. Часть 1.
Технические средства обучения: Компьютер. Медиапроектор.
Этапы урока
Деятельность учителя
Деятельность учащихся
Формирование УУД
1. Мотивация к учебной деятельности.
Цель: создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность
Эмоциональный настрой на урок.
Дети, вам повезло? (Да!)
В классе светло? (Да!)
Прозвенел уже звонок? (Да!)
Уже закончился урок? (Нет!)
Только начался урок? (Да!)
Хотите учиться? (Да!)
Значит можно всем садиться!
Настраиваемся на урок.
– Будем учиться оценивать свою деятельность. Прочитайте.
– внимательно;
– правильно;
– дружно;
– быстро.
Правильно формулировать собственное мнение.
(Р/УУД).
2. Актуализация знаний.
Цель: обеспечение готовности учащихся к включению в продуктивную обучающую деятельность, повторение изученного материала, необходимого для «открытия нового знания».
На карточках задание.
– Посмотрите.
– Будете работать в парах.
– 1 вариант решает первое выражение,
– 2 вариант – второе выражение, и т.д.
Задание: Решите числовые выражения, впишите буквы и расшифруйте слово:
6 + 9 = 15 в
11 – 3 = 8 й
8 + 4 = 12 с
16 – 6 = 10 о
9 + 2 = 11 т
13 – 8 = 5 с
4 + 8 = 12 о
14 – 7 = 7 в
На экране:
– Поднимите руки, кто закончил.
– Прочитайте слово, которое получилось.
– Как вы понимаете слово «свойство»?
– Найдите два похожих выражения.
– Чем они похожи?
– Чем отличаются?
– Какое свойство вспомнили?
– Это свойство поможет нам решать более сложные числовые выражения.
– А сейчас, те дети, у которых получилось слово «свойство» поставьте себе 4 балла (по количеству правильно решённых выражений).
Если вы допустили 1-2 ошибки – 2 балла.
– Оценим работу. Мы работали:
– Дети решают числовые выражения, расшифровывают слово.
– Поясняют.
– от перестановки слагаемых сумма не изменится
– Внимательно, дружно, быстро, правильно.
Выделение и осознание того, что уже пройдено (Р/УУД).
Смыслообразование (Л/УУД).
Слушать и понимать речь других (К /УУД)
3. Самоопределение к деятельности.
Цель: обсуждение цели урока.
Практическая работа.
– Возьмите конверты.
– Выложите 4 круга, затем 3 треугольника и 7 квадратов.
– Сколько всего фигур выложили?
– Как их удобнее сосчитать?
4 + 3 + 7 записываю на доске
Вывод: оказывается, эту сумму можно посчитать разными способами.
– Чему мы будем учиться?
– Складывать числа в любом порядке.
4. Постановка целей.
Цель: проговаривание детьми цели и темы урока.
Стр. 44.
– Прочитайте цель урока.
– Формулируют цель урока.
Определять и формулировать цель деятельности на уроке (Р/УУД).
5. Работа по теме урока.
Цель: обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы.
№ 1. Коллективное выполнение с комментированием.
– Прочитайте задание.
– Сформулируйте задание.
– Чем похожи все числовые выражения?
– Чем отличаются?
– Какое свойство применили?
Вывод: результат сложения не изменится, если поменять слагаемые местами.
– Это свойство называют переместительным. (поменяли местами). Экран
– Обратимся к геометрическим фигурам.
– Как удобно сосчитать их?
– Как показать, что это действие выполним первым?
– Что скажете о результатах сложения?
– Как складывали?
– Оказывается, это тоже свойство. В математике – это свойство называют сочетательным. Экран
– Прочитайте вывод: результат сложения не изменится, если соседние слагаемые заменить их суммой.
– Выполняют задание, проговаривая свойства сложения.
– Заключим в скобки.
– Одинаковые.
– Соседние слагаемые заменили их суммой.
Проводить анализ учебного материала (П /УУД)
Ориентироваться в учебнике (П /УУД)
Слушать и понимать речь других (К /УУД)
6. Первичное закрепление.
Цель: обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации.
На экране – числовое выражение:
6 + 7 + 8 + 9 + 3 + 4 + 1 + 2 =
– Объясните как вы будете вычислять, используя оба свойства сложения. ( в любом порядке, как удобнее).
Итог на экране:
(6+4) +(7+3) + (8+2) + (9+1) =
– Почему так объединяли?
– На листочках записано выражение: 14 + 15+ 6 +5 вычислите, используя оба свойства.
– Вычислите, работая в парах.
– Начнут решение 1 вариант.
– Проверим. Экран.
– Что помогло быстро найти значение выражения?
– Оцените свою работу, поставьте 1 балл, если всё правильно.
– Как работали?
-Устно комментируют.
– Чтобы получить круглое число.
Работают в парах.
(14+6) + (15+5)=40
– Перестановка слагаемых и замена слагаемых суммой.
– Быстро, дружно, правильно, внимательно
Слушать и понимать речь других (К /УУД)
Определять правила работы в паре (Л /УУД)
7. Решение задач.
Цель: совершенствовать умение решать задачи.
– А сейчас будете работать над задачей на стр.47 № 6.
– Прочитайте задачу.
– Прочитайте условие. Вопрос.
– О чём задача?
– Кто участвовал в турнире?
– Что известно?
– Что нужно узнать?
– Какая это задача?
– Попробуйте сами записать решение и ответ.
– Проверим. Поставь 2 балла, если решил сам и правильно.
– Как мы работали?
9. Рефлексия.
Цель: выявление качества и уровня овладения знаниями.
– Ребята, какова тема урока?
– Какую цель вы поставили вначале урока?
– Как вы считаете, достигли ли цели?
– Почему?
– Где нам это пригодится?
Осознание результатов своей учебной деятельности.
Самооценка результатов своей работы и работы всего класса.
– Познакомились со свойствами, научились их применять.
– При работе с большими числами.
Устанавливать связь между целью деятельности и ее результатом (Л /УУД)
Совместно с учителем и одноклассниками давать оценку деятельности на уроке (Р/УУД).
9. Подведение итогов.
Цель: анализ и оценка успешности достижения цели;
Спасибо за сотрудничество! Урок окончен.
Источник
Учитель: Рябова Н.М.
Этапы урока | Деятельность учителя | Деятельность учеников | Формируемые УУД |
I. Мотивация к учебной деятельности Цель: – создание условий для возникновения у учеников внутренней потребности включения в учебную деятельность; | Эмоциональный настрой на урок. -Долгожданный дан звонок. Начинается урок. -Улыбнулись друг другу-(слайд) Давайте приступим к работе . И пусть интересным будет урок. А девиз нашего урока: «Будьте внимательны и у вас все получится» (слайд) Нас на уроке ждут великие дела.(слайд) | Проговаривание правил сотрудничества | Определять и проявлять правила поведения при сотрудничестве. (Л /УУД). Правильно формулировать собственное мнение. (Р/УУД). |
II. Актуализация знаний Цель: – обеспечение готовности учащихся к включению в продуктивную обучающую деятельность, повторение изученного материала, необходимого для «открытия нового знания». | Организация живого диалога – Какое сейчас время года ? (осень). -Кто любит осень? -Какое сегодня число? (19) – Что вы можете сказать о числе 19? ( двузначное, состоит из 1 дес. и 9 ед.). -Почему число 19-двузначное? (в его записи использовано 2 цифры). -Представьте число 19 в виде суммы разрядных слагаемых. (19=10+9) – распределите числа на 2группы(слайд) 4, 27, 83, 9, 16, 5, 72, 31, 94. -по какому признаку вы это сделали? -Какие числа мы называем однозначными? -Почему числа называем двузначными? – Укажите состав чисел. -Прочитайте числа в порядке возрастания, (убывания). -Прочитайте правильно числовые выражения и найдите их значения: 60+8=, 68-60=, 68-8= 30+(5+2)=, 90-(6+4). (слайд) -Правило: Действия, записанные в скобках, выполняются первыми. -Найдите периметр треугольника со сторонами 4см, 5см, 6см – Что такое периметр?(слайд) –Периметр-это сумма длин сторон многоугольника. | Ведение живого диалога: свободно говорят, высказывают свою точку зрения | Выделение и осознание того, что уже пройдено (Р/УУД). Смыслообразовани (Л/УУД). Слушать и понимать речь других (К /УУД) |
III. Постановка целей, задач урока, мотивационная деятельность учащихся. Цель: – обсуждение затруднений, проговаривание цели урока, темы. | – Прочитайте слова: слагаемое, уменьшаемое, разность, слагаемое, вычитаемое, сумма. (слайд) – Кто мне поможет разделить эти слова на группы? (I – компоненты действия сложения, II – компоненты действия вычитания) (слайд) – Назовите их.(Компоненты при сложении называются: слагаемое, слагаемое, сумма. Компоненты при вычитании называются: уменьшаемое, вычитаемое, разность) -Как вы думаете, к какой группе можно отнести слово «свойство…» ? (к I группе) – Кто догадался, какая у нас сегодня тема урока? (свойства сложения) (слайд) – Чему мы будем учиться на уроке? (познакомимся со свойствами сложения и будем их применять при нахождении значений числовых выражений). -С каким свойством сложения вы уже знакомы? ( с переместительным) -сравни: 30+8*8+30, 7+10*10+7 (слайд) – Как читается переместительный закон сложения? (От перестановки слагаемых сумма не изменяется) -Не вычисляя, составьте верные числовые равенства. ( 50 + 8 = * + 50, 5 + 40 = 40 + * (слайд) * + 8= 8 + 2) – Зачем нужно знать это свойство при вычислениях? ( Легче к большему числу прибавить меньшее). Запись с помощью букв: а+в=в+а (слайд) -Работа по учебнику с.44, №1. (взаимопроверка) – А найдите значение этого числового выражения: 6 + 7 + 8 + 9 + 3 + 4 + 1 + 2 = (слайд) -У кого это задание вызвало затруднение? -Проблема. ( Не достаточно знаний, чтобы легко и быстро справиться с заданием.) | Вспоминают названия компонентов при сложении. Анализируют слова, деля их на группы. Формулируют цель урока. | Определять и формулировать цель деятельности на уроке (Р/УУД). Высказывать свое предположение на основе учебного материала (Р/УУД). Проводить классификацию, указывая на основание классификации (П /УУД) Ориентироваться в своей системе знаний (определять границы знания/незнания) (П /УУД) Уметь с достаточной полнотой и точностью выражать свои мысли (К /УУД) |
IV. Первичное усвоение новых знаний Цель: – обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы. Организация исследовательской деятельности, выведение алгоритма. | – Давайте вместе добудем эти знания! (рассмотреть с помощью кружков разного цвета еще одно свойство сложения) (слайд) (5+3)+2=5+(3+2) 10 = 10 Вывод: Результат сложения не изменится, если два соседних слагаемых заменить их суммой. Это сочетательный закон сложения. (на доске). – (а+в)+с=а+(в+с) – Эти два закона работать могут вместе. Давайте вернемся к нашему числовому выражению и решим его. – Какие у вас будут предложения? (Можно применить переместительное свойство сложения, а затем сочетательное свойство сложения). (6+4)+(7+3)+(8+2)+(9+1)=40 (слайд) Вывод: Используя оба свойства сложения, можно складывать числа в любом порядке. -С какими свойствами сложения мы с вами познакомились? (ответы детей) | Решают проблему, обсуждая и выдвигая гипотезы в совместной деятельности, сравнивают, анализируют, осуществляют поиск необходимой информации Выполняют задание, проговаривая свойства сложения. Составляют буквенную запись свойств сложения. Работают с учебником в парах. Выполняют задания | Проводить анализ учебного материала (П /УУД) Ориентироваться в учебнике, тетради (П /УУД) Определять правила работы в паре (Л /УУД) Слушать и понимать речь других (К /УУД) Отличать верно выполненное задание от неверного (Р/УУД). |
V.Первичное закрепление Цель: – обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации. Выполнение заданий с проговаривание в громкой речи. Запись с помощью буквенных выражений. | (Работа в паре) Дополните формулировку свойств пропущенными словами. От _________ слагаемых сумма ___________. Результат _______________не изменится, если соседние _____________заменить их суммой. Чтобы к сумме двух чисел прибавить ___________, можно к первому числу прибавить сумму __________ и третьего числа. Игра «Помоги героям вспомнить свойства» – В каком из примеров использовано сочетательное свойство? (переместительное) 3 + (2 + 1) = (3 + 2) + 1 21 – 17 = 17 – 21 15 + 18 = 18 + 15 4 + 9 = 13 46 + 0 = 46 – А для чего нам нужно знать свойства сложения? (для быстрого, рационального вычисления выражений) — Работа по учебнику: с.44, правило. с.45, № 3. (устно) Найти значения числовых выражений: ( с проговариванием в громкой речи ) 6+9+4+1= 17+8+3+2= | Участвуют в диалоге. Выполняют задания в парах, ведут обсуждение, учатся принимать на себя ответственность за результат учебного труда. | Определять правила работы в паре (Л /УУД) Владеть диалогической формой речи в соответствии с грамматическими и синтаксическими нормами родного языка. (К /УУД) |
VI. Самостоятельная работа с самопроверкой. Цель: – умение применять правило в самостоятельной деятельности. | – Самостоятельно найдите рациональный способ вычисления суммы, пользуясь свойствами сложения. -Какими свойствами вы будете пользоваться? 1)Работа по карточке(дифференцированные задания). Карточка №1 15+6+7+5+4+3= 40+7+20+3= 82+6+8+4= 26+13+4+7 Карточка №2 7+9+5+1+3+5= 50+6+40+4= 32+7+8+3= Карточка № 3 7+8+3+2= 15+9+5+1= САМОПРОВЕРКА. (слайд) №1. 40,70,100,50 №2. 30,100,50. №3. 20,30. –Кто выполнил без ошибок? -Кто допустил ошибки? 2)Найдите значения числовых выражений (на время): (слайд) 7+9+3+1=(7+3)+(9+1)=20 15 + 8 + 2= 15 + (8 + 2) = 25 1 + 39 + 20 = (1 + 39) + 20 = 60 63 + 14 + 6 = 63 + (14 + 6) = 83 12 + 8 + 10 = (12 + 8) + 10 = 30 6+5+4=(6+4)+5=15 ПРОВЕРКА: САМОПРОВЕРКА. – Кто допустил ошибки при вычислении? – У кого ошибок нет? – Оцените свою работу.(смайлик на полях) 2) Применение нового знания при решении задач. 1)Построить ломаную из трех звеньев: 6см, 2см, 4см.Найти ее длину? 2)Учебник.С.45, № 5. Задача. ( Решение: 30+30+20+20= (30+20)+(30+20)=100(мм)-периметр четырехугольника. 100мм=10см Ответ:10см . | Самостоятельное решение в тетради. Осуществляют самоконтроль и самооценку своей работы. | Отличать верно выполненное задание от неверного (Р/УУД). Осуществлять самоконтроль (Р/УУД). Оценивать усваиваемое содержание (Л /УУД) |
VII. Подведение итогов учебного занятия. Рефлексия деятельности Цель: – анализ и оценка успешности достижения цели; выявление качества и уровня овладения знаниями. | ВОПРОСЫ: -Ребята, какова была тема урока? -Какую цель вы ставили перед собой? -Достигли ли поставленной цели? – В чём ценность нового знания? -Оцените свою работу на уроке.(смайлики) Весело звенит звонок. Вот и закончился наш урок. Благодарю за внимание. | Осознание результатов своей учебной деятельности; Самооценка результатов своей работы и работы всего класса. | Устанавливать связь между целью деятельности и ее результатом (Л /УУД) Совместно с учителем и одноклассниками давать оценку деятельности на уроке (Р/УУД). |
VIII Домашнеезадание. Комментировать. | С. 44,правило, с.45, № 4, с. 46, №1.-применить изученные свойства сложения при нахождении значения числовых выражений. |
Резер
