Какие свойства сложения есть и примеры


Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
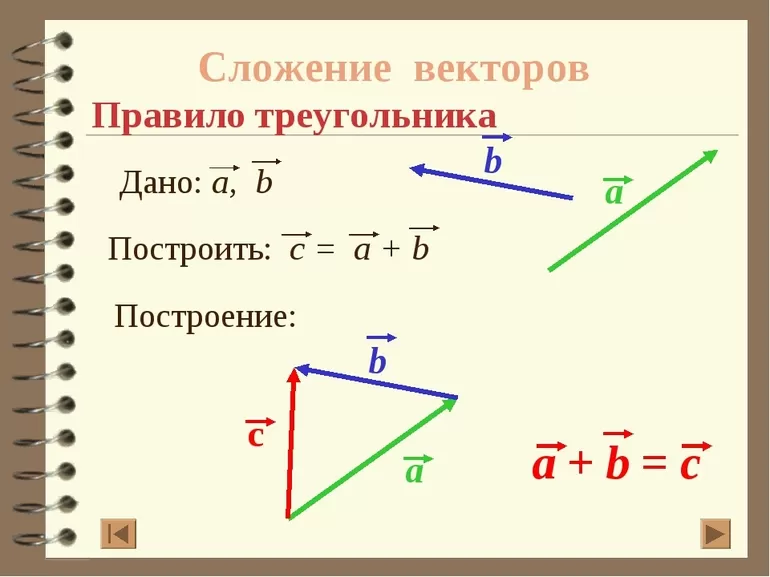
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
Сложение натуральных чисел.
Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
Сумма — это сложение чисел. Знак плюс “+”.
В буквенном виде этот пример будет выглядеть так:
a+b=c
Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.
Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:
4+3=3+4
Называется такое свойство слагаемых переместительным законом сложения.
Переместительный закон сложения.
От перемены мест слагаемых сумма не меняется.
В буквенной записи переместительный закон выглядит так:
a+b=b+a
Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:
(1+2)+4=7
Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:
1+(2+4)=7
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:
(1+2)+4=1+(2+4)
Это свойство сложения называется сочетательным законом сложения.
Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a+b)+c=a+(b+c)
Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30
Свойство сложения с нулем.
При сложении числа с нулем, в результате сумма будет тем же самым числом.
3+0=3
0+3=3
3+0=0+3
В буквенном выражение сложение с нулем будет выглядеть так:
a+0=a
0+a=a
Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:
 Второй вариант таблицы сложения.
Второй вариант таблицы сложения.
 Если посмотрим на таблицы сложения, видно как работает переместительный закон.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.
В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.
В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.
Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.
Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a
Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22
Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.
Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921
Источник
План урока:
Устные вычисления в пределах 100
Переместительное и сочетательное свойства сложения
Решение задач на нахождение неизвестного слагаемого
Математика вокруг нас
Задачи повышенной сложности
Здравствуйте! Начнем урок с загадок.
Это медвежонок-праздник.
Очень любит сладкий мед.
Озорник он и проказник,
Не всегда ему везет.
Ребята, вы догадались, о ком идет речь? Конечно, о Винни – Пухе!

Источник
Медвежонку лучший друг –
Это знают все вокруг!
Не бычок, и не волчок,
А веселый …?

Источник
Да, веселый Пятачок!
Сегодня Винни – Пух и Пятачок будут учиться вместе с нами. Они приготовили для урока тетради в клеточку, вооружились цветными ручками, фломастерами и карандашами. Ну что ж, за дело!
Устные вычисления в пределах 100
Чтобы научиться быстро и правильно вычислять устно, нужно хорошо уметь раскладывать двузначные числа на разрядные слагаемые. Например, в числе 29 – 2 десятка и 9 единиц . 29 = 20 + 9. Удобно это записывать так:
Разложите числа: 69, 56, 66, 31, 77 на разрядные слагаемые.

69 = 60 + 9
56 = 50 + 6
66 = 60 + 6
31 = 30 + 1
77 = 70 + 7
Запомни правило!

Решим вместе такие примеры:


Переместительное и сочетательное свойства сложения
Ребята, запомним свойства сложения! С их помощью вычислять получается гораздо быстрее и легче.

Источник

Источник
Эти свойства показывают, что мы можем переставлять слагаемые, как удобно, а значит, позволяют упрощать вычисления.

7 + 9 + 3 + 1 + 8 + 6 + 2 + 4 + 3
16 + 12 + 4 + 8
Будем использовать оба свойства. Можно складывать в любом порядке.
Посмотрите внимательно на примеры! Какие два числа в сумме дают круглое число? Соединим их дугой. Внизу под дугой подпишем результат.

Решите самостоятельно примеры. Соединяйте дугой слагаемые (так удобнее и быстрее):
21 + 3 + 9 + 37
13 + 4 + 34 + 6 + 7

Есть другой способ записи: с использованием скобок.
Решим еще несколько примеров. Вычислим устно удобным способом следующие суммы:
20 + 8 + 40 + 2 = (20 + 40) + (8 + 2) = 60 + 10 = 70
30 + 1 + 9 + 60 = (30 + 60) + (1 + 9) = 90 + 10 = 100

Задачи на нахождение неизвестного слагаемого
Ребята, помогите Пятачку и Винни – Пуху найти вторую половинку правила:

Это правило пригодится нам, чтобы верно решить задачу.

Посмотрите, Пятачок и Винни – Пух идут друг к другу в гости. Дорожка длиной 80 м. Пятачок прошел до встречи 30 м. Сколько метров прошел до встречи Винни – Пух?
Схема нам поможет понять задачу.
Сколько прошел Пятачок? 30 м.
А сколько прошел Винни – Пух? Не знаем.
Из чего состоит длина дорожки? Из расстояния, которое прошли Пятачок и Винни – Пух вместе.
Это можно записать так: 30 + ? = 80 (м)
С1 + С2 = С
Что неизвестно? Второе слагаемое.
Как его найти? С2 = С – С1
Решение: 80 – 30 = 50 (м) – прошел до встречи Винни – Пух.
Ответ: 50 метров.
Математика вокруг нас
Мы с вами даже не подозреваем о том, что математика – всюду! Давайте вместе с Пятачком и Винни – Пухом отправимся в гости к Кролику и попробуем отыскать математику в самых простых привычных вещах. Понаблюдаем за формой, цветом, размером предметов.

Источник
Вот мы с вами у дома Кролика.
Ребята, скажите, какой формы клумбы в цветнике?

Источник
Верно, мы с вами видим четырехугольники и круг. Посмотрите, как здорово Кролик подобрал цветы для своей клумбы: здесь и белые ромашки, и желтые бархатцы, и красные гвоздики. Ярко и празднично.

Источник
А это маленький огород Кролика. Какие геометрические фигуры вы увидели? Какого они размера?

Кролик пригласил своих гостей на чаепитие. Какие геометрические фигуры вы видите в орнаменте и узорах на тарелках и чашках?

Тарелка
Винни Пух
Верно, мы видим круги, многоугольники, волнистые и ломаные линии, овалы и точки.
Винни – Пух и Пятачок испекли пирог для чаепития. Он получился вкусным, потому что все было сделано по рецепту.

Вот видите, ребята, и здесь пригодилась математика!
Ну что ж, пора нашим героям отправляться в лесную школу. Их там уже давно ждут.

Источник
Посмотрите на часы, которые висят на стене. Определить, который час, нам поможет математика. Маленькая часовая стрелка показывает на число 10, а большая минутная стрелка – на 12 (здесь она начинает свой отсчет). Значит, сейчас ровно 10 часов 00 минут.
Задачи повышенной сложности
Ребята, поможем нашим героям справиться с задачами повышенной сложности. Научим их и научимся сами рассуждать, логически мыслить.

Источник
В лесной школе прошла математическая олимпиада. В финал олимпиады вышли две белки и два зайца. Все вместе они решили 11 задач: каждый – разное количество. Кто решил больше задач: зайцы или белки, если один заяц решил задач больше всех, а другой заяц – меньше всех.
Для решения этой задачи надо подбирать разные числа и проверять, подходят ли они.
Для удобства начертим таблицу.

Нужно в сумме набрать 11 так, чтобы все слагаемые были разные. Пусть первый заяц решит всего 1 задачу (меньше всех). Белки решат разное количество, например, 2 и 3. Ну а второй заяц решит больше всех – это 5.
1 + 2 + 3 + 5 = 11. В сумме получилось 11 задач.
Значит, зайцы решили: 1 + 5 = 6, белки решили: 2 + 3 = 5.
6 > 5
Ответ: зайцы решили задач больше, чем белки.
Сегодня в лесной школе все с увлечением мастерили фигурки в технике оригами.

Источник
У Пятачка, Винни – Пуха и Кролика есть 3 бумажные фигурки – оригами: лиса, птичка и кораблик. По одной – у каждого. Известно, что у Пятачка – не кораблик, у Кролика и Пятачка – не лиса. У кого какая фигурка?
Давайте рассуждать вместе! Чертим таблицу.

Поставим знак « – »в ячейке напротив героев сказки. Мы знаем, что у Пятачка – не кораблик и не лиса. У него – птичка, значит, у Кролика птички нет, и ему остается кораблик. А у Винни – Пуха – фигурка лисы.

Молодцы, ребята! Приходите еще, порешаем вместе! А теперь проверьте свои знания. Всем пока!
Источник
Содержание
Определение действия сложение и компоненты сложения
Переместительный и сочетательный законы сложения
Правило прибавления слагаемого к сумме или суммы к слагаемому
Изменение суммы чисел с изменением слагаемых
Сложение однозначных чисел
Сложение многозначного и однозначного чисел
Сложение двух многозначных чисел в столбик
Сложение в столбик нескольких многозначных чисел
Онлайн-репетиторы по всем школьным предметам. Подготовка к ОГЭ и ЕГЭ
Записаться
Как вы уже знаете, любое натуральное число представляет собой единицу или собрание нескольких единиц. Так вот, мы можем взять несколько чисел и объединить все единицы, которые их составляют, в одно большое собрание. Число, которое получилось в результате этого объединения, называется суммой.
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Определение
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
На записи действие сложения обозначается знаком + (плюс). То есть, если записано3+2+5, то это означает, что нам нужно найти сумму этих трех чисел: 3, 2 и 5. Сумма записывается обычно справа от слагаемых после знака = (равно): 3+2+5 = 10.
Сумма чисел состоит (слагается, складывается, – можно говорить по-разному) из двух или более слагаемых. Понятно, что сумма всегда больше любого ее слагаемого.
Слагаемые – это не что иное, как состав числа, обозначающего сумму этих слагаемых.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Действие сложения можно выполнить всегда. Действительно, так как натуральный ряд бесконечен, то мы всегда можем любые числа этого ряда объединить в другое, какое угодно большое число.
Действие сложения всегда имеет единственный результат. Действительно, если мы, к примеру, отметим на координатном луче с началом в точке O и единичным отрезком 1 см отрезок OA длиной 5 см, а потом построим еще один отрезок AB длиной 7 см, то у нас получится только единственный отрезок OB длиной 12 см.
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Есть два основных закона суммы, из которых следуют остальные ее свойства:
- переместительный закон сложения,
- сочетательный закон сложения.
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.
Например, в каком бы порядке мы ни складывали числа 2, 3 и 5, результат неизменно будет 10:
Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
То же самое будет, если мы заменим слагаемые 3 и 5, или 2 и 5 их суммами:
или
Из этих законов вытекает правило прибавления слагаемого к сумме или суммы к слагаемому.
Правило
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325+(12+64+5) = 325+81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
325+12 = 337;
337+64 = 401;
401+5 = 406
или
325+64 = 389;
389+12 = 401;
401+5 = 406.
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
(54+240+189)+37 = 483+37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
54+37 = 91;
91+240 = 331;
331+189 = 520
или
240+37 = 277;
277+54 = 331;
331+189 = 520.
Изменение суммы чисел с изменением слагаемых
Чтобы понять, как изменится сумма чисел, если изменить одно или несколько ее слагаемых, нужно вспомнить, что сумма представляет собой собрание всех единиц, из которых состоят слагающие ее числа. Поэтому, легко можно понять, что:
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Если увеличить одно из слагаемых на какое-то число (на какое-то количество единиц), а другое уменьшить на это же число (на это же количество единиц), то в результате сумма не поменяется.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Например, для нахождения суммы 5+2 нужно к числу 5 присоединить 2 единицы. Тогда получим 5+2=7. А если нужно к числу 7 прибавить число 8, или другими словами, найти сумму 7+8, то после присоединения к 7 единиц числа 8 получим 1 десяток единиц и еще 5 единиц, то есть, число 15.
Сложение однозначных чисел – это первый и очень важный шаг в освоении этого арифметического действия. Если хорошо выучить все результаты сложения однозначных чисел между собой, тогда вы сможете намного быстрее складывать в уме любые числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
Допустим, нам нужно найти сумму чисел 88 и 5.
Способ 1.
Представим число 88 в виде суммы 80+8 и прибавим к ней число 5. После этого, найдем сумму однозначных чисел 8 и 5, получится 13. Прибавим этот результат к числу 80. Число 13 – это 10+3, поэтому мы к 8 десяткам прибавляем 1 десяток, получаем 9 десятков, или число 90, а к нему прибавляем еще 3 (оставшиеся от числа 13), и получим 93.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
Способ 2.
Замечаем, что если к 88 прибавить 2, то получим полный десяток, то есть, число 90. Тогда представляем число 5 в виде суммы 2+3; число 2 складываем с 88, получаем замеченное нами ранее число 90. Добавляем к нему оставшееся число 3, и получаем результат 93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сумма многозначных чисел удобно вычисляется, если использовать так называемое сложение в столбик.
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Этот способ простой, и он помогает не запутаться во время вычисления, не допустить ошибки. Но, чтобы складывать быстро, как я и говорил раньше, вам нужно очень хорошо знать все попарные суммы однозначных чисел.
Итак, допустим, что нам нужно найти сумму : 5728+803
Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. плюс. У нас получилась такая запись:
Теперь нам нужно сложить между собой единицы каждого разряда, начиная с первого: сперва простые единицы, потом десятки единиц, потом сотни единиц и т.д. Результаты этих сложений записываем под чертой в том разряде, единицы которого мы складывали.
Начинаем с простых единиц: 8+3=11. У нас получилось число 11, то есть, 1 десяток и 1 единица. 1 единицу мы записываем под чертой в разряде единиц, а 1 получившийся десяток нужно будет дополнительно прибавить к сумме единиц разряда десятков. Чтобы не забыть совершить это действие, мы пишем над цифрами разряда десятков маленькую цифру 1 или ставим там точку.
Про подобное действие обычно говорят: «один пишем, один в уме» , то есть, оставляем в памяти, чтобы не забыть добавить при следующем действии.
Далее переходим к десяткам. У первого слагаемого 2 единицы разряда десятков, а у второго , поэтому: 2+0=2. Мы помним, что после сложения простых единиц у нас образовался дополнительно 1 десяток, поэтому к этому результату добавляем еще единицу: 2+1=3. У нас получилось 3 десятка, поэтому записываем цифру 3 под чертой в разряде десятков.
Следующими идут сотни: 7+8=15. Первым делом проверяем, не нужно ли нам дополнительно добавлять единицу? В нашем случае нет, потому что на предыдущем шаге при сложении десятков мы получили однозначное число. Поэтому, пишем под чертой в разряде сотен цифру 5. И у нас получилось дополнительно 10 сотен, то есть, 1 тысяча единиц. Значит, нам нужно отметить эту получившуюся 1 тысячу как дополнительную, поставив маленькую цифру 1 над цифрами разряда тысяч.
В разряде тысяч у первого слагаемого стоит цифра 5, а у второго ничего не стоит. Но мы помним, что при отсутствии разрядов в начале числа (слева) нули не пишутся, но подразумевается, что в этих разрядах по единиц. Поэтому мы находим сумму 5+0=5, т.е. 5 единиц разряда тысяч и добавляем к ней дополнительную 1 единицу тысяч, полученную после сложения разрядов сотен. 5+1=6. Записываем эту цифру под чертой в разряде тысяч.
После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Этим способом так же легко можно найти сумму нескольких многозначных чисел.
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».
Сложив десятки этих трех чисел, мы получим 4+0+5=9 единиц разряда десятков. Добавив 2 десятка единиц, которые у нас были «в уме», получаем 11, то есть, 10 десятков и ещё 1 десяток. Под чертой мы записываем цифру 1 в разряде десятков, а так как 10 десятков – это не что иное как 1 сотня, то мы отмечаем «единицу в уме», то есть, ставим над всеми тремя числами в разряде сотен маленькую цифру 1.
Теперь складываем сотен первого числа, 6 сотен второго и 3 сотни третьего. Получается 9 сотен. Добавляем 1 сотню, которая была «в уме» после сложения всех десятков, и у нас выходит 10 соте
