Какие свойства света подтверждают эффект комптона
Фотон и его свойства | |
Фотон – материальная, электрически нейтральная частица, квант электромагнитного поля (переносчик электромагнитного взаимодействия). | |
Основные свойства фотона
| |
Энергия фотона:. Согласно теории относительности энергия всегда может быть вычислена как , Отсюда – масса фотона. Импульс фотона . Импульс фотона направлен по световому пучку. | |
Наличие импульса подтверждается экспериментально: существованием светового давления. | |
Давление света | |
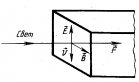
В 1873 г. Дж. Максвелл, исходя из представлений об электромагнитной природе света, пришел к выводу: свет должен оказывать давление на препятствие(благодаря действию силы Лоренца; на рисунке v – направление скорости электронов под действием электрической составляющей электромагнитной волны). |
|
Квантовая теория света объясняет световое давление как результат передачи фотонами своего импульса атомам или молекулам вещества. Пусть на поверхность абсолютно черного тела площадью S перпендикулярно к ней ежесекундно падает N фотонов: . Каждый фотон обладает импульсом . Полный импульс, получаемый поверхностью тела, равен . Световое давление: | |
При падении света на зеркальную поверхность удар фотона считают абсолютно упругим, поэтому изменение импульса и давление в 2 раза больше, чем при падении на черную поверхность (удар неупругий). |
|
Это давление оказалось ~4.10-6 Па. Предсказание Дж. Максвеллом существования светового давления было экспериментально подтверждено П. Н.Лебедевым, который в 1900 г. измерил давление света на твердые тела, используя чувствительные крутильные весы. Теория и эксперимент совпали. Опыты П. Н. Лебедева — экспериментальное доказательство факта: фотоны обладают импульсом | |
Эффект Комптона (1923) | |
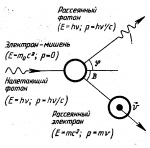
А. Комптон на опыте подтвердил квантовую теорию света. С точки зрения волновой теории световые волны должны рассеиваться на малых частицах без какого-либо изменения частоты излучения, что опытом не подтверждается. При исследовании законов рассеяния рентгеновских лучей А. Комптон установил, что при прохождении рентгеновских лучей через вещество происходит увеличение длины волны рассеянного излучения по сравнению с длиной волны падающего излучения. Чем больше угол рассеяния, тем больше потери энергии, а следовательно, и уменьшение частоты (увеличение длины волны). Если считать, что пучок рентгеновских лучей состоит из фотонов, которые летят со скоростью света, то результаты опытов А. Комптона можно объяснить следующим образом. Законы сохранения энергии и импульса для системы фотон – электрон: |
|
где m0c2 – энергия неподвижного электрона; hv – энергия фотона до столкновения; hv‘ – энергия фотона после столкноВЕНИЯ, P и p’ – импульсы фотона до и после столкновения; mv – импульс электрона после столкновения с фотоном. | |
Решение системы уравнений для энергии и импульса с учетом того, что дает формулу для измерения длины волны при рассеянии фотона на (неподвижных) электронах: | |
где – так называемая комптоновская длина волны. | |
Корпускулярно-волновой дуализм | |
Конец XIX в.: фотоэффект и эффект Комптона подтвердили теорию Ньютона, а явления дифракции, интерференции света подтвердили теорию Гюйгенса. | |
Таким образом, многие физики в начале XX в. пришли к выводу, что свет обладает двумя свойствами: | |
| |
Чем больше v, тем ярче выражены квантовые свойства света и менее – волновые. | |
Итак, всякому излучению присущи одновременно волновые и квантовые свойства. Поэтому то, как проявляет себя фотон – как волна или как частица,—зависит от характера проводимого над ним исследования. | |
Источник
Согласно квантовой гипотезе Планка-Эйнштейна свет частотой n испускается, распространяется и поглощается веществом отдельными порциями (квантами), энергия которых eо=hn (h – постоянная Планка). Эти локализованные в пространстве дискретные световые кванты, движущиеся со скоростью с распространения света в вакууме, получили название фотонов. Таким образом, распространение света можно рассматривать не как непрерывный волновой процесс, а как поток частиц – фотонов. Доказательством этих квантовых (корпускулярных) представлений о свете, как о потоке частиц, являются фотоэффект и эффект Комптона.
Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения. Явление внешнего фотоэффекта и его закономерности объяснены на основе квантовой теории фотоэффекта, согласно которой каждый квант света поглощается только одним электроном.
Энергия hn падающего на металл фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетевшему фотоэлектрону кинетической энергии, то есть по закону сохранения энергии:
(уравнение Эйнштейна для внешнего фотоэффекта).
Из этого уравнения следует, что максимальная кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности, то есть от числа фотонов. Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается, то при некоторой частоте n=n0 кинетическая энергия фотоэлектронов станет равной нулю и в том случае энергия фотона hn0 равна работе выхода А, из чего следует, что n0=А/h (частота n0 носит название красной границы фотоэффекта). При частоте n<n0 фотоэффекта не будет.
Масса и импульс фотона.Согласно квантовой гипотезе Планка-Эйнштейна, распространение света можно рассматривать как поток часииц – фотонов, энергия которых e=hn . Тогда из уравнения Эйнштейна взаимосвязи массы и энергии E=mc2 следует, что масса фотона:
.
Фотон движется со скоростью света с, поэтому импульс р фотона:
.
Полученные выражения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой характеристикой света – его частотой n (или его длиной волны l).
Корпускулярные свойства света проявляются в эффекте Комптона.
Эффектом Комптона называется увеличение длины волны коротковолнового электромагнитного излучения при его упругом рассеянии на свободных электронах вещества. Опыты Комптона показали, что разность длин волн рассеянного (l’) и падающего (l) электромагнитного излучения, то есть величина Dl=l’–l не зависит от длины волны l падающего излучения и природы рассеивающего вещества (РВ), а определяется только углом рассеяния q, то есть углом между направлениями лучей до и после рассеяния (рис. 29):
, где–комптоновская длина волны.
Эффект Комптона не укладывается в рамки волновой теории света, и его объяснение дано на основе квантовых представлений о природе света. Если рассматривать излучение, как поток фотонов, то эффект Комптона – это результат упругого столкновения рентгеновских фотонов со свободными электронами рассеивающего вещества. В процессе этого столкновения фотон передает электрону часть своей энергии, что ведет к увеличению длины волны при рассеянии фотона.
(На рисунке 29 введены следующие обозначения: p и p’ – импульсы фотона до и после рассеяния; pe– импульс электрона после рассеяния на нем фотона).
Исходя из законов сохранения импульса и энергии
для упругого столкновения двух частиц (рис. 29) – налетающего фотона с покоящимся свободным электроном вещества, было получено следующее выражение для величины Dl:
, где пм.
Это выражение для величины Dl, полученное на основе корпускулярных представлений о свете, оказалось аналогично приведенному выше выражению для величины Dl, полученному Комптоном экспериментально.
Следовательно, эффект Комптона является экспериментальным доказательст-вом проявления корпускулярных свойств света как потока частиц – фотонов. Итак, рассмотренные явления фотоэффекта и эффекта Комптона служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов, а, с другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую природу света. Таким образом, свет, обладая одновременно корпускулярными и волновыми свойствами, проявляет так называемый корпускулярно-волновой дуализм.
Тема 14. Тепловое излучение
Излучение света телами, обусловленное их нагреванием, называется тепловым излучением. Количественно тепловое излучение характеризуется спектраль-ной плотностью энергетической светимости тела,т.е. мощностью излучения с единицы площади поверхности тела в интервале частот единичной ширины:
, где
– энергия излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от n до n + dn .
Спектральную плотность энергетической светимостиможно представить в виде функции длины волны l , то есть в виде Rl,T, причем:
.
С помощью этой формулы можно перейти от Rn,Tк Rl,Tи наоборот.
Зная спектральную плотность энергетической светимости, можно вычислить интегральную энергетическую светимостьRT:
.
Способность тел поглощать падающее на них излучение характеризуется спектральной поглощательной способностью Аn,T :
,
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от n до n + dn , поглощается телом.
Тело, способное поглощать полностью при любой температуре всё падающее на него излучение любой частоты, называется черным телом. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице ().
Закон Кирхгофа. Кирхгоф установил, что отношение спектральной плотности энергетической светимости Rn,Tк спектральной поглощательной способности Аn,T не зависит от природы тела; оно является для всех тел универсальной функцией rn,T частоты n (или длины волны l) и температуры Т:
.
Для черного тела , поэтому из закона Кирхгофа вытекает, что универсальная функция Кирхгофа rn,T – это спектральная плотность энергетической светимости Rn,T черного тела. Тогда выражение для интегральной энергетической светимости черного тела Reможно записать в виде:
.
Энергетическая светимость черного тела Re зависит только от температуры.
Закон Стефана – Больцмана. Согласно закону Стефана – Больцманаэнергетическая светимость черного тела Re зависит от температуры Т следующим образом: , где s – постоянная Стефана – Больцмана.
Закон смещения Вина. Из экспериментальных кривых зависимости функции rl,T от длины волны l при различных температурах (рис. 30) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют ярко выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн.
Согласно закону смещения Вина, зависимость длины волны lmax , соответствующей максимуму функции rl,T, от температуры имеет вид: , где b – постоянная Вина.
Это выражение называют законом смещения Вина, так как оно показывает смещение положения максимума функции rl,T с изменением температуры Т .
Источник
Как мы знаем, Альберт Эйнштейн в 1905 году предложил для объяснения фотоэффекта так называемую концепцию фотонов. Позже, в 1922 г., американский физик А.Комптон провел серию опытов и подтвердил ее экспериментально. Он провел исследования упругого рассеяния коротковолнового рентгеновского излучения на свободных электронах вещества (или электронах, слабо связанных с атомами) и открыл, что длина волны рассеянного изучения не соответствует ранее принятой волновой теории. Согласно ей, электроны, испытывающие воздействие периодического поля световой волны, совершают вынужденные колебания на частоте волны и поэтому излучают рассеянные волны той же частоты, следовательно, длина волны излучения при рассеянии не должна меняться.
На иллюстрации представлена схема прохождения монохроматического рентгеновского излучения с длиной волны λ0, которое исходит из трубки R, через свинцовую диафрагму. После прохождения его направляют узким пучком на слой рассеивающего вещества (алюминия, графита). Затем получившееся излучение, рассеянное под углом θ, анализируют при помощи спектрографа рентгеновских лучей S с дифракционной решеткой в виде кристалла K, помещенного на поворотный столик. Результаты опыта показывают, что в рассеянном излучении длина волны Δλ увеличивается в зависимости от угла рассеяния.
∆λ=λ-λ0=2Λsin2θ2.
Здесь параметр Λ=2,43·10–3 нм выражает так называемую комптоновскую длину волны, которая не имеет связи с свойствами рассеивающего вещества.
Определение 1
Если излучение является рассеянным, то в нем помимо спектральной линии с длиной волны λ присутствует и несмещенная линия, длина волны которой равна λ0.
Соотношение интенсивности обеих линий связано с тем, какое вещество использовано в качестве рассеивающего.
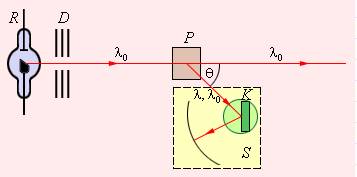
Рисунок 5.3.1. Эксперимент Комптона (схематическое изображение).
Следующие иллюстрации показывают, как распределяется интенсивность в спектре рассеянного излучения в зависимости от угла рассеивания.
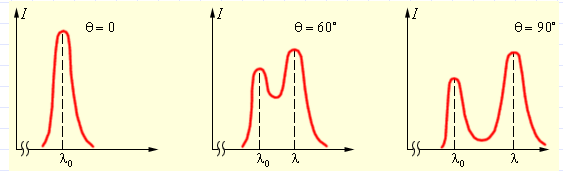
Рисунок 5.3.2. Распределение интенсивности в рассеянном излучении.
Объяснение эффекта с помощью квантовых представлений
Эффект Комптона был объяснен в 1923 году самим Комптоном и П. Дебаем, которые работали независимо друг от друга. В обоих случаях в основе объяснения лежат квантовые представления.
Определение 2
Если излучение является потоком фотонов, то эффект Комптона происходит из-за упругого столкновения свободных электронов вещества с рентгеновскими фотонами. Рассеивающие вещества имеют слабую связь между ядрами атомов и электронами, поэтому можно считать, что они имеют в составе свободные электроны. При столкновении им передается часть энергии фотонов и часть импульса.
Пример 1
Рассмотрим подробнее процесс упругого столкновения налетающего фотона с импульсом p0 =hν0c и энергией E0=hν0с электроном, у которого энергия покоя составляет Ee0=mc2. После того, как частицы столкнутся, направление движения фотона изменяется, т.е. происходит рассеяние, после чего импульс фотона становится равен p=hνc, а энергия – E=hν<E0. Что касается электрона, то, согласно релятивистской формуле, его энергия становится равной Ee=pe2c2+m2c4(буквой pe обозначен приобретенный импульс). Запишем формулу закона сохранения:
E+Ee0=E+Ee.
Иначе говоря, hυ0+mc2=hυ+pe2c2+m2c4.
Также нам понадобится закон сохранения импульса:
p0→=p→+pe→.
С помощью теоремы косинусов мы можем перевести его в скалярную форму:
pe2=hυ0c2+hυc2-2h2c2υ0υ cos θ.
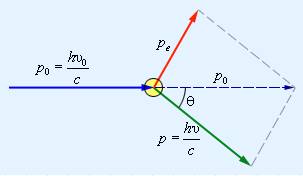
Рисунок 5.3.3. Распределение импульсов при столкновении налетающего фотона и покоящегося электрона
Теперь возьмем эти два соотношения (законы сохранения импульса и энергии), проведем несложные преобразования, исключив pe, и получим следующее:
mc2υ0-υ=hυ0υ(1-cos θ).
Перейдем от частот к волнам υ0=cλ0, υ=cλ. У нас получится выражение, совпадающее с формулой Комптона, которая была получена при эксперименте:
∆λ=λ-λ0=hmc(1-cos θ)=2hmcsin2θ2.
Проведенные теоретические расчеты, использующие квантовые представления, помогают не только объяснить эффект Комптона, но и вывести формулу нахождения длины волны с помощью фундаментальных констант m, h, c:
Λ=hmc=2,426·10-3 нм.
Почему длина части волн не изменяется?
Согласно данным опыта, в излучении после рассеяния кроме смещенной линии есть и несмещенная, длина волны излучения которой совпадает с первоначальной. Ее наличие можно объяснить тем, что часть фотонов взаимодействует с электронами, крепко связанными с ядрами атомов. Тогда происходит обмен энергии и импульса с атомом в целом, а не только с электроном. Поскольку атом весит значительно больше, то переданная энергия фотона очень мала, следовательно, длина волны λ рассеянного излучения остается практически неизменной.
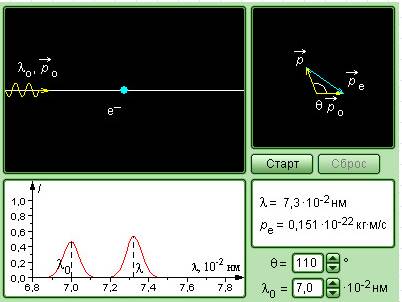
Рисунок 5.3.4. Модель комптоновского рассеяния.
Источник
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 5. Квантовая физика
Концепция фотонов, предложенная А. Эйнштейном в 1905 г. для объяснения фотоэффекта, в 1922 г. получила экспериментальное подтверждение в опытах американского физика А. Комптона. Комптон исследовал упругое рассеяние коротковолнового рентгеновского излучения на свободных (или слабо связанных с атомами) электронах вещества. Открытый им эффект увеличения длины волны рассеянного излучения, названный впоследствии эффектом Комптона, не укладывается в рамки волновой теории, согласно которой длина волны излучения не должна изменяться при рассеянии. Согласно волновой теории, электрон под действием периодического поля световой волны совершает вынужденные колебания на частоте волны и поэтому излучает рассеянные волны той же частоты.
Схема Комптона представлена на рис. 5.2.1. Монохроматическое рентгеновское излучение с длиной волны λ0, исходящее из рентгеновской трубки R, проходит через свинцовые диафрагмы и в виде узкого пучка направляется на рассеивающее вещество-мишень P (графит, алюминий). Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей S, в котором роль дифракционной решетки играет кристалл K, закрепленный на поворотном столике. Опыт показал, что в рассеянном излучении наблюдается увеличение длины волны Δλ, зависящее от угла рассеяния θ:
где Λ = 2,43·10–3 нм – так называемая комптоновская длина волны, не зависящая от свойств рассеивающего вещества. В рассеянном излучении наряду со спектральной линией с длиной волны λ наблюдается несмещенная линия с длиной волны λ0. Соотношение интенсивностей смещенной и несмещенной линий зависит от рода рассеивающего вещества.
| Рисунок 5.3.1. Схема эксперимента Комптона |
На рис. 5.3.2 представлены кривые распределения интенсивности в спектре излучения, рассеянного под некоторыми углами.
| Рисунок 5.3.2. Спектры рассеянного излучения |
Объяснение эффекта Комптона на основе квантовых представлений о природе излучения было дано в 1923 году независимо друг от друга А. Комптоном и П. Дебаем. Если принять, что излучение представляет собой поток фотонов, то эффект Комптона есть результат упругого столкновения рентгеновских фотонов со свободными электронами вещества. У легких атомов рассеивающих веществ электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными. В процессе столкновения фотон передает электрону часть своей энергии и импульса в соответствии с законами сохранения.
Рассмотрим упругое столкновение двух частиц – налетающего фотона, обладающего энергией E0 = hν0 и импульсом p0 = hν0 / c, с покоящимся электроном, энергия покоя которого равна
Фотон, столкнувшись с электроном, изменяет направление движения (рассеивается). Импульс фотона после рассеяния становится равным p = hν / c, а его энергия E = hν < E0. Уменьшение энергии фотона означает увеличение длины волны. Энергия электрона после столкновения, в соответствии с релятивистской формулой (см. § 4.5), становится равной где pe – приобретенный импульс электрона. Закон сохранения записывается в виде
или
Закон сохранения импульса
можно переписать в скалярной форме, если воспользоваться теоремой косинусов (см. диаграмму импульсов, рис. 5.3.3):
| Рисунок 5.3.3. Диаграмма импульсов при упругом рассеянии фотона на покоящемся электроне |
Из двух соотношений, выражающих законы сохранения энергии и импульса, после несложных преобразований и исключения величины pe можно получить
mc2(ν0 – ν) = hν0ν(1 – cos θ).
Переход от частот к длинам волн приводит к выражению, которое совпадает с формулой Комптона, полученной из эксперимента:
Таким образом, теоретический расчет, выполненный на основе квантовых представлений, дал исчерпывающее объяснение эффекту Комптона и позволил выразить комптоновскую длину волны Λ через фундаментальные константы h, c и m:
Как показывает опыт, в рассеянном излучении наряду со смещенной линией с длиной волны λ наблюдается и несмещенная линия с первоначальной длиной волны λ0. Это объясняется взаимодействием части фотонов с электронами, сильно связанными с атомами. В этом случае фотон обменивается энергией и импульсом с атомом в целом. Из-за большой массы атома по сравнению с массой электрона атому передается лишь ничтожная часть энергии фотона, поэтому длина волны λ рассеянного излучения практически не отличается от длины волны λ0 падающего излучения.
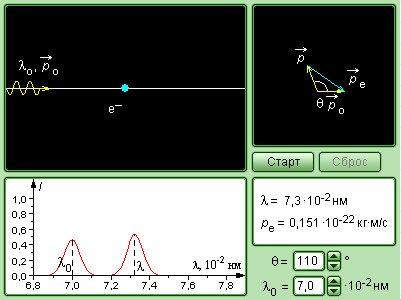 |
Модель. |
Источник