Какие свойства у овала

Виктор Чебыкин

Введение

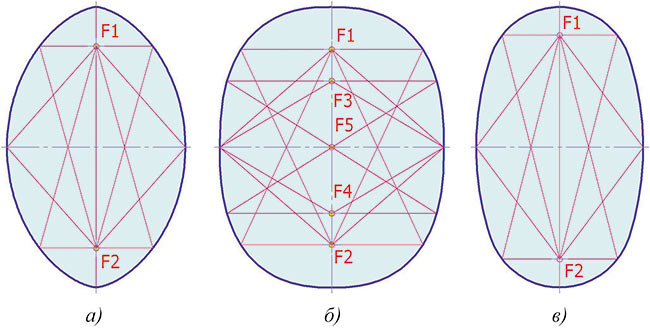
Продолжая рассмотрение эллипсовидных овальных кривых (Э.О.К.), начатое в статьях [1], [2] и [3], остановимся еще на трех: циклоидальный овал; гиперэллипс Ламе; овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1). При этом также попробуем классифицировать их и другие Э.О.К. на три группы: гиперовалы, гипоовалы и гипергипоовалы. В последнем разделе речь идет об идентификации Э.О.К. 

Рис. 1. Овальные кривые: а — циклоидальный овал; б — гиперэллипс Ламе;
в — овальная кривая Rr (гиперовал)

Циклоидальный овал

Циклоидальный овал (рис. 1а и 2) — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая, полученная в результате зеркальной стыковки двух «арок» циклоиды. Циклоида — плоская трансцендентная кривая; это траектория точки окружности, катящейся по прямой линии [4].

Одним из свойств циклоидального овала является наличие двух фокусов, имеющих строго определенное расположение.

Фокусы могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. Это свойство совпадает с аналогичным у кривой R­1, описанной в [3]. Точки падения этих лучей на кривую, так же как у кривой R­1, являются характерными — в них меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный.

Еще одно свойство циклоидального овала: размеры некоторых элементов овала могут быть вычислены как произведение радиуса производящей окружности данной циклоиды или размеров полуосей с определенными константами. О последних и пойдет речь далее.

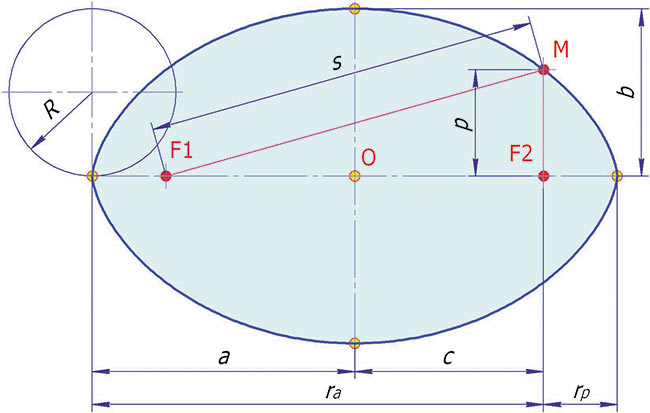
Рис. 2. Циклоидальный овал

Элементы овала (рис. 2):

• R — радиус производящей окружности цик­лоиды;
• a — большая полуось;
• b — малая полуось;
• с — фокальный радиус (полурасстояние между фокусами);
• p — малый фокальный луч;
• s — большой фокальный луч;
• rp — перифокусное расстояние (минимальное расстояние от фокуса до точки на овале);
• ra — апофокусное расстояние (максимальное расстояние от фокуса до точки на овале).

Константы циклоидального овала:

1. Константа соотношения осей овала
   Ксо1 = а/b = p/2;
2. Фокальная константа
   Vco = c/R ≈ 2,259 360 664 54…;
3. Перифокусная константа
   PVco = rp/R ≈ 0,882 231 989 04…;
4. Апофокусная константа
   AVco = ra/R ≈ 5,400 953 318 13…;
5. Эксцентриситет­константа
   Eco = с/a ≈ 0,719 176 835 98…;
6. Константа малого фокального луча
   Lco = p/R ≈ 1,270 684 347 65…;
7. Константа большого фокального луча
   GLco = s/R ≈ 4,693 983 506 71…

Попытка найти в литературе и Интернете сведения по константам циклоидальных овалов ничем не увенчалась, поэтому названия констант и их обозначения автор предложил свои. Ну и значения констант, за исключением первой, пришлось определить самому.

Теперь отнесем этот овал к одной из групп: гиперовалы (от греч., гипер —  «над, выше»); гипоовалы (гипо — «под, ниже»); гипергипоовалы.

Построим по полюсам данного овала эллипс и увидим, что он будет описанным по отношению к овалу, а овал соответственно — вписанным в эллипс. Исходя из этого, циклоидальный овал является гипоовалом. Циклоидальные кривые используются в технике: маятник Гюйгенса; кривая кратчайшего спуска; циклоидальные передачи и редукторы; кулачки и эксцентрики…

Гиперэллипс Ламе

Кривая показана на рис. 1б. Такую форму и такое название кривая имеет, если степени m и n в формуле кривой Ламе больше 2.

Гиперэллипс, так же, как овал Кассини (который описан в [3]), имеет два основных оптических фокуса и три дополнительных. Само название его говорит о том, к какой группе следует отнести этот овал — к гиперовалам.

Рис. 3. Разновидности овальных кривых Rr

Гипоэллипс Ламе, показанный в [3], где он был назван просто кривой Ламе, в формуле имеет степени m и n меньше 2. При степенях m и n равных 2 кривая Ламе является эллипсом. В случае если одна из степеней больше, а другая меньше 2, мы имеем гипергипоэллипс (рисунок не показан). Если по полюсам этого овала построить эллипс, то можно увидеть, что кривые имеют как точки касания, так и точки пересечения между собой.

Овальная кривая Rr

Овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1в и 3). Эти овалы хорошо известны тем, кто учился в докомпьютерную эру (по аналогии с «до н.э.» имеем «до к.э.»). Ими пользовались для упрощенного изображения эллипсов на чертежах. Сейчас, по понятным причинам, необходимость в этом отпала. В технике эти овалы все же используются — кулачки, эксцентрики и т.п.

На рис. 1в изображена овальная кривая Rr (гиперовал), а на рис. 3  —сразу три вида овалов: внутренний — гиперовал; наружный — гипоовал; средний — гипергипоовал. Тонкими линиями показаны соответствующие этим овалам эллипсы, которые помогают определить принадлежность кривых к той или иной группе.

Классификация кривых, описанных в статье [3]:

• овал Кассини — гиперовал;
• кривая Ламе (показанная) — гипоовал;
• кривые R­0 и R­1 — гипоовалы;
• кривая R­2: верхняя часть — гиперовал, нижняя — гипоовал.

Идентификация эллипсовидных овальных кривых

Итак, для идентификации предлагаются следующие кривые: эллипс, овал Кассини, гиперэллипс Ламе; гипоэллипс Ламе; гипергипоэллипс Ламе; овал R­0; овал R­1; циклоидальный овал; гиперовал Rr; гипоовал Rr; гипергипоовал Rr. Зная геометрию и свойства данных кривых, классификацию можно выполнить визуально, однако иногда  некоторые из них бывают очень схожи.

Идентификацию лучше проводить в той CAD­программе, в которой эти кривые созданы. Автор для построения и идентификации кривых использовал  программу КОМПАС.

При поочередном входе в режим редактирования кривых можно сразу распознать эллипс и все овалы по сопрягаемым дугам окружностей, группу которых определяем сопряжением с эллипсом. Все остальные кривые при редактировании покажут, что построены с помощью кривой Безье.

Оставшиеся кривые сначала необходимо разбить на группы в соответствии с нашей классификацией путем сопряжения с соответствующими им эллипсами.

В группе гипергипоовалов окажется только гипергипоэллипс, так как гипергипоовал Rr распознан уже на первой стадии идентификации.

Далее рассмотрим группу гипоовалов. Поскольку гипоовал Rr также распознан на первой стадии, в ней остаются: кривая R­0; кривая R­1; гипоэллипс Ламе; циклоидальный овал. Последний распознаем с помощью эксцентриситет­константы циклоидального овала (пригодилась!). Для этого поочередно для каждой кривой рассчитываем фокальный радиус, умножая размер большой полуоси на эксцентриситет­константу Eco. Тот овал, в котором пучок из восьми лучей, выпущенных из фокуса и отраженных от кривой, соберется в противоположном фокусе, и будет циклоидальным овалом. Для распознавания оставшихся трех гипоовалов рассмотрим три возможных сценария идентификации. Все зависит от количества фокусов у гипоэллипса Ламе. Первый вариант — кривая Ламе имеет четыре фокуса (например, при сочетании параметров: a/b = 7/10; n = m = 1,7). В этом случае удается распознать все кривые: бесфокусную R­0, двухфокусную R­1 и четырехфокусную  кривую Ламе.  Второй вариант — кривая Ламе бесфокусная (например, при сочетании параметров: a/b = 8/10; n = m = 1,7). При этом сможем распознать только R­1. Кривая R­0 и гипоэллипс будут трудноразличимыми. Третий вариант — кривая Ламе имеет два фокуса (например, при сочетании параметров: a/b = 8/10; n = 1,7 и m=1,9). Выявить при этом удастся  только кривую R­0. Различить R­1 и гипоэллипс Ламе можно по форме кривых и расположению фокусов… 

Осталось разобраться с гиперовалами. После первой стадии идентификации, где был определен гиперовал Rr, их у нас осталось два: овал Кассини и гиперэллипс Ламе. Для идентификации их в первую очередь необходимо выровнять масштабированием размеров овалов по высоте. Далее нужно определить положение фокусов (тех, которые фигурируют в определении овала Кассини) относительно центра и нанести их. Оптические фокусы овалов использовать нельзя — у них другие координаты. Та кривая, на которой будет соблюдено следующее условие: произведение расстояний от любой точки кривой до фокусов есть величина постоянная, — и есть овал Кассини. Если степени гиперэллипса Ламе равны 2,5 и более, то кривые хорошо различимы визуально — кривая Ламе более угловатая.

Выводов делать не будем. Главное, что почти все точки над «о» расставлены. 

Библиографический список

1. Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы. Справочник // Инженерный журнал. 2012. № 11. С. 31­33.
2. Чебыкин В.Г. Особенности технологии врезки люков и патрубков в обечайки резервуаров // Технология машиностроения. 2013. № 1. С. 33­35.
3. Чебыкин В. А не замахнуться ли нам на Габриеля нашего Ламе? // САПР и графика. 2013. № 8. С. 92, 94­95.
4. Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982. Т.5. С. 809.

САПР и графика 3`2014

Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а…г).

Рис. 13.45

Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О1О2 (см. рис. 13.46.а, и рис. 13.46.в), а центры О3 и О4 определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.

Рис. 13.46

Построение овала с соприкасаю­щимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 01 радиусом, равным, например, расстоянию между их центрами, проводят дуги окруж­ностей до пересечения в точках О2и О3.

Рисунок 3.44

Если из точек О2и О3провести прямые через центры О и O1, то в пересечении с опорными окружнос­тями получим точки сопряжения С, C1, D и D1. Из точек О2и О3 как из центров радиусом R2 проводят дуги сопряжения.

Построение овала с пересека­ющимися опорными окружностями(задача также имеет множество решений) (рис. 3.45). Из точек пе­ресечения опорных окружностей С2 и О3 проводят прямые, например, через центры О и O1 до пересечения с опорными окружностями в точках сопряжения С, С1 D и D1, а ра­диусами R2, равными диаметру опорной окружности,— дуги со­пряжения.

Рисунок 3.45 Рисунок 3.46

Построение овала по двум задан­ным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На верти­кальной оси откладываются отре­зок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пе­ресечения с отрезком АС в точке Е1. К середине отрезка АЕ1 восстанавливают перпендикуляр и отмечают точки его пересечения с осями ова­ла O1 и 02. Строят точки O3 и 04, симметричные точкам O1 и 02 от­носительно осей CD и АВ. Точки O1 и 03 будут центрами опорных ок­ружностей радиуса R1, равного от­резку О1А, а точки O2 и 04 — цент­рами дуг сопряжения радиуса R2, равного отрезку О2С. Прямые, со­единяющие центры O1 и 03 с O2 и 04 в пересечении с овалом опреде­лят точки сопряжения.

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

2. пересекаются;

3. не пересекаются.

Рассмотрим первый случай. Строят отрезок OO1=2R, параллельный оси Х, на его концах (точки О и О1) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R1=2R. Из точек пересечения вспомогательных окружностей О2 и О3 строят дуги CD и C1D1 соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C1D1 обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса