Какие свойства у параболы

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ: наглядно.

Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая.
b — второй коэффициент, который отвечает за смещение параболы от центра координат.
с — свободный член, который соответствует координате пересечения параболы с осью ординат.

График квадратичной функции — парабола, которая имеет следующий вид для y = x2:

Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:

x	-2	-1	1	2
y	4	1	1	4

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.

График функции y = –x2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

x	-2	-1	1	2
y	-4	-1	-1	-4

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

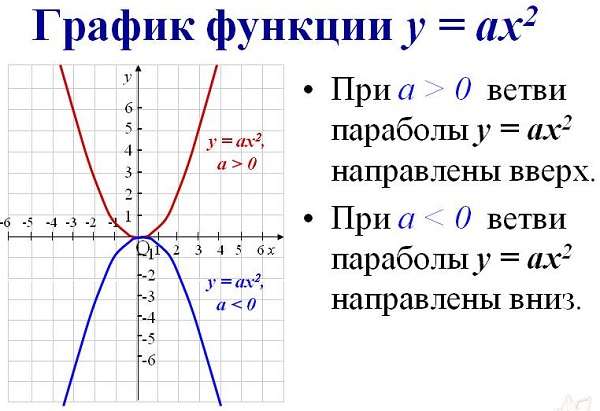
Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.

Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.

Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.

Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 – 4ac, который даст нам информацию о количестве корней квадратного уравнения.

Рассмотрим три случая:

Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:

Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:

Если a > 0, то график выглядит как-то так:

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax2 + bx + c.

Разберем общий алгоритм на примере y = 2×2 + 3x – 5.

Как строим:

Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
Найдем дискриминант квадратного трехчлена 2×2 + 3x – 5.

D = b2 – 4ac = 9 – 4 * 2 * (-5) = 49 > 0

√D = 7

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

2×2 + 3x – 5 = 0

Координаты вершины параболы:

Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
Нанести эти точки на координатную плоскость и построить график параболы:

Уравнение квадратичной функции имеет вид y = a * (x – x₀)2 + y₀

Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2×2 + 3x – 5 при а = 1, то второй коэффициент является четным числом.

Рассмотрим пример: y = 2 * (x – 1)2 + 4.

Как строим:

Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:

построить y = x2,
умножить ординаты всех точек графика на 2,
сдвинуть его вдоль оси ОХ на 1 единицу вправо,
сдвинуть его вдоль оси OY на 4 единицы вверх.

Построить график параболы для каждого случая.

Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)

Рассмотрим следующий пример: y = (x – 2) * (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x – 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab =(-2) * (1)= -2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Чтобы не запутаться во всех графиках, приходите вместе с ребенком на бесплатный урок математики в современную школу Skysmart: порисуем параболы на интерактивной онлайн-доске, разберемся в самых коварных формулах и покажем, что математика может быть увлекательным путешествием.

Источник

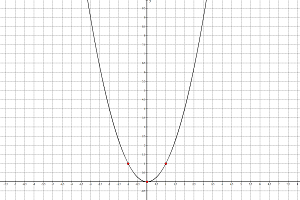
Парабола свойства и график квадратичной функции

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Парабола свойства и график квадратичной функции

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
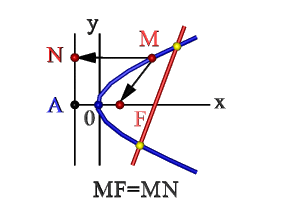
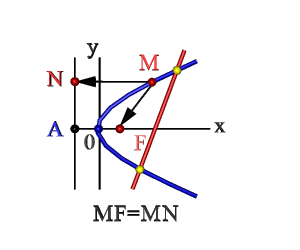
Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

y2 = 2 * p * x,

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x2 + b x + c (узнаваемый шаблон: y = x2).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Парабола свойства и график квадратичной функции

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Парабола свойства и график квадратичной функции

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

x0 = -b / (2 * a),
y0 = y (x0).

Пример.

Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

х = -16 / (2 * 4) = -2,
y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

Смещение параболы

Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).

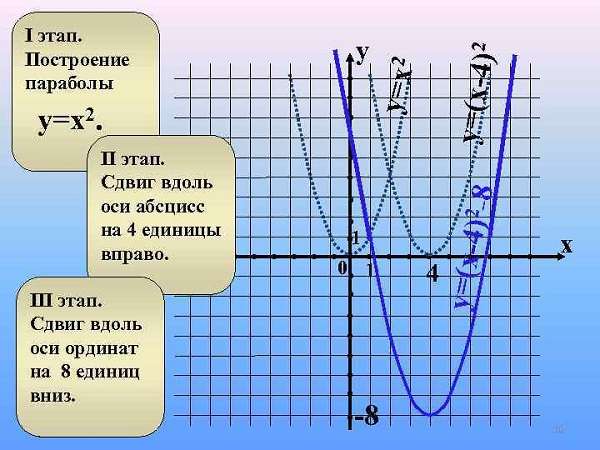
Парабола свойства и график квадратичной функции

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

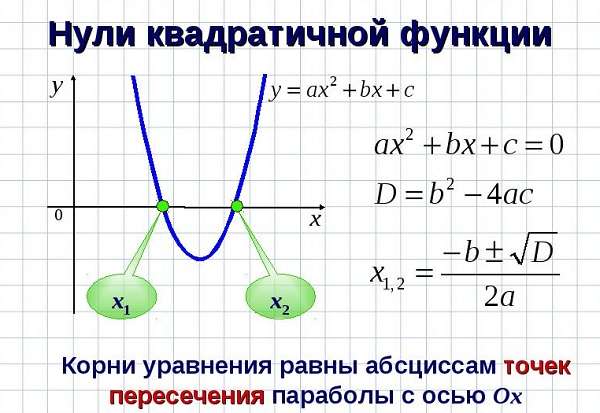
Парабола свойства и график квадратичной функции

Анализируя выражения и уравнения, можно увидеть следующее:

Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

D = (b2 4 * a * c).

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
D = 0, то х1, 2 = -b / (2 * a),
D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

определить направление ветвей,
найти координаты вершины,
найти пересечение с осью ординат,
найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

а = 1, следовательно, ветви направлены вверх,
координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
с осью ординат пересекается в значении у = 4,
найдем дискриминант: D = 25 — 16 = 9,
ищем корни:

Х1 = (5 + 3) / 2 = 4, (4, 0),
Х2 = (5 — 3) / 2 = 1, (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:

а = 3, следовательно, ветви направлены вверх,
координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
с осью у будет пересекаться в значении у = -1,
найдем дискриминант: D = 4 + 12 = 16. Значит корни:

Х1 = (2 + 4) / 6 = 1, (1,0),
Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

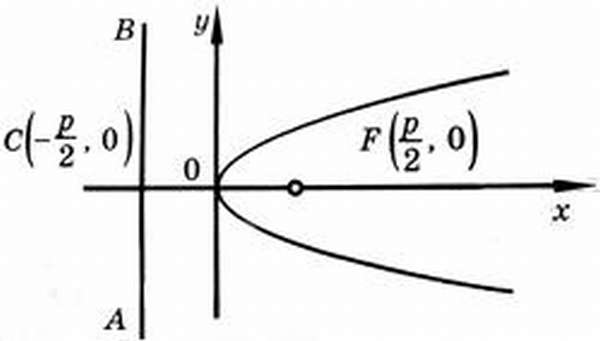
Парабола свойства и график квадратичной функции

Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Парабола свойства и график квадратичной функции

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

Источник

График функции $y=x^2$

Чтобы построить график функции $y = x^2$, найдём несколько точек, удовлетворяющих этому равенству. Для удобства координаты точек запишем в виде таблицы:

$x$		$dfrac{1}{3}$	$dfrac{1}{2}$	$1$	$2$	$3$
$y = x^2$		$dfrac{1}{9}$	$dfrac{1}{4}$	$1$	$4$	$9$

Заметим, что $(- x)^2 = x^2$. Поэтому график будет симметричен относительно оси $Oy$.

Отметим полученные точки в декартовой системе координат (см. рисунок 1) и соединим их плавной линией (см. рисунок 2).

Отметим полученные точки на координатной плоскости	Соединим их плавной линией

Рис. 1 Рис. 2

Видно, что график «прижимается» к оси $Ox$ при маленьких значениях аргумента и начинает «быстро расти» при больших.

Функция $y = x^{2}$ называется элементарной квадратичной функцией, а её график $-$ параболой.

График функции $y = ax^2$

Если коэффициент $a > 0$, то график $y = ax^2$ получается из графика $y = x^2$ либо вертикальным растяжением вдоль оси $Oy$ (при $a > 1$), либо сжатием (при $0 < a < 1$). Изобразим для примера графики $y = 2x^2$ и $y = dfrac{1}{2}x^2$ (см. рисунки 3 и 4).

$y = 2x^2$	$y = dfrac{1}{2}x^2$

Рис. 3 Рис.4

Если же $a < 0$, то график функции $y = ax^2$ можно получить из графика $y = |a|x^2$, отобразив его симметрично относительно оси $Ox$. Построим графики функций $y = – x^2$, $y = -2x^2$ и $y = – dfrac{1}{2}x^2$ (см. рисунки 5,6,7). Как и в случае элементарной квадратичной функции, графики функций $y = ax^2$, $aneq0,$ являются параболами.

$y = – x^2$	$y = -2x^2$	$y = – dfrac{1}{2}x^2$

Рис. 5 Рис.6 Рис.7

График квадратичной функции

График функции $y = ax^2 + bx + c$ $(aneq0)$ можно построить, преобразовав квадратный трёхчлен и применив геометрические преобразования к графику элементарной функции $y = x^2$. Для этого выделим из квадратного трехчлена

$ax^2 + bx + c$

полный квадрат, то есть представим его в виде

$a(x – x_0)^2 + y_0.$

График функции

$y = a(x – x_0)^2 + y_0$

получается из графика функции $y = x^2$ растяжением в $a$ раз вдоль оси $Oy$ (при $0<a<1$ фактически происходит сжатие, а при отрицательных значениях $a$ ещё и отображение симметрично относительно оси $Ox$), затем смещением на $x_0$ единиц вправо вдоль оси $Ox$ и, наконец, перемещением на $y_0$ единиц вдоль оси $Oy$. В итоге точка $(0;0)$ переместится в точку $(x_0;y_0)$.

Таким образом, график любой квадратичной функции $y = ax^{2} + bx + c$, где $a neq 0,$ является параболой. Точка с координатами $(x_0;y_0)$ называется вершиной параболы $y = a(x – x_0)^2 + y_0$.

Отметим, что функция $y = x^2$ является частным случаем квадратичной функции при $a=1,$ $b=c=0.$

$blacktriangleright$ Пример. Построим график функции $y = 2x^2 – 4x – 6$.

Решение. Выделив полный квадрат, получим $y = 2(x – 1)^2 – 8$. Цепочка преобразований графика продемонстрирована на рисунке 8. В итоге получилась парабола с вершиной в точке $(1;-8)$.

Построим график $y = 2x^2$	Сместим его вправо на 1	Сместим вниз на 8

Рис. 8

График квадратичной функции $y = ax^2 + bx + c$ пересекает ось $Oy$ в точке $(0; c)$ и ось $Ox$ в точках $(x_{1,2};0)$, где $x_{1,2}$ — корни квадратного уравнения $ax^2 + bx + c = 0$ (если это уравнение не имеет действительных корней, то соответствующая парабола не пересекает ось абсцисс $Ox$).

Например, парабола $y = 2x^2 – 4x – 6$ пересекает оси в точках $(0; -6)$, $(-1; 0)$ и $(3; 0)$.

Утверждение

Вершина параболы квадратичной функции $y = ax^2 + bx + c$ находится в точке с координатами

$left(- dfrac{b}{2a}; dfrac{4ac – b^2}{4a}right).$

Вынесем из первых двух слагаемых выражения $(ax^2 + bx + c)$ множитель $a$ за скобку:

$ a cdot left(x^2 + dfrac{b}{a}cdot xright) + c, $

замечаем, что если к выражению, стоящему в скобках, добавить число $left(dfrac{b}{2a}right)^2$, то получится полный квадрат:

$ x^2 + dfrac{b}{a}cdot x + left(dfrac{b}{2a}right)^2 = x^2 + 2xcdot dfrac{b}{2a} + left(dfrac{b}{2a}right)^2 = left(x + dfrac{b}{2a}right)^2. $

Заменяем выражение в скобках на $left(x + dfrac{b}{2a}right)^2 – left(dfrac{b}{2a}right)^2$ и в итоге получаем:

$ ax^2 + bx + c = acdotleft(left(x + dfrac{b}{2a}right)^2 – left(dfrac{b}{2a}right)^2right) + c = acdotleft(x + dfrac{b}{2a}right)^2 + c – dfrac{b^2}{4a}. $

То есть квадратичную функцию можно представить в виде

$y=acdotleft(x + dfrac{b}{2a}right)^2 + c – dfrac{b^2}{4a},$

отсюда следует, что вершина параболы находится в точке $left(- dfrac{b}{2a}; dfrac{4ac – b^2}{4a}right)$.

Итак, перечислим все сведения о параболе:

$1)$ при $a>0$ $-$ ветви параболы направлены вверх, при $a<0$ ветви параболы направлены вниз;

$2)$ координаты вершины параболы $left(-dfrac b{2a};dfrac{4ac-b^2}{4a}right)$;
$3)$ $(0;c)$ $-$ точка пересечения с осью ординат $Oy$;
$4)$ при $D>0$ парабола дважды пересекает ось абсцисс $-$ в точке $(x_1;0)$ и точке $(x_2;0)$;

при $D=0$ парабола имеет ровно одну общую точку с осью абсцисс, эта точка есть вершина параболы;

при $D<0$ парабола не пересекает ось абсцисс.

Постройте графики следующих функций:

$1)$ $y=x^2-2x-3$;
$2)$ $y=2x^2+4x-5$;
$3)$ $y=x^2+5x-6$.

$1)$ Выделим полный квадрат:

$y=x^2-2x-3=x^2-2x+1-4=(x-1)^2-4.$

Значит, график данной функции можно получить параллельным переносом параболы $y=x^2$ на $1$ единицу вправо вдоль оси $Ox$ и на $4$ единицы вниз вдоль $Oy$ (см. рисунок 9).

Определите знаки коэффициентов $a$, $b$, $c$ функции $y = ax^2 + bx + c$ и знак дискриминанта $D$ по предложенным графикам:

Рис.12

У параболы, выделенной красным цветом, ветви направлены вверх, значит, коэффициент $a>0$. Эта парабола пересекает ось ординат выше нуля, значит, коэффициент $c>0$. Парабола не пересекает ось абсцисс, поэтому $D<0$. Вершина параболы находится правее нуля, то есть абсцисса вершины положительна. Следовательно, $-dfrac b{2a}>0$, а поскольку $a>0$, значит, $b<0$.

У параболы, выделенной синим цветом, ветви направлены вниз, значит, $a<0$. Эта парабола пересекает ось ординат ниже нуля, значит, коэффициент $c<0$. Парабола не пересекает ось абсцисс, поэтому $D<0$. Вершина параболы находится левее нуля, то есть абсцисса вершины отрицательна. Следовательно, $-dfrac b{2a}<0$, а поскольку $a<0$, значит, $b<0$.

У параболы, выделенной зелёным цветом, ветви направлены вниз, значит, $a<0$. Эта парабола пересекает ось ординат ниже нуля, значит, $c<0$. Парабола пересекает ось абсцисс дважды, поэтому $D>0$. Вершина параболы находится правее нуля, следовательно, $-dfrac b{2a}>0$, а поскольку $a<0$, значит, $b>0$.

Источник

Парабола

Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.

Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус на оси так, чтобы начало координат помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через расстояние от фокуса к директрисе, тогда у фокуса будут координаты , .

Для произвольной точки параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а и поэтому:

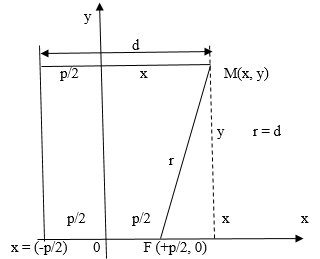
Парабола

Рис. 1

(1)

– каноническое уравнение параболы.

Что такое вершина параболы

Важно!
Если вы не уверены, что справитесь с работой самостоятельно, обратитесь к профессионалам. Сдадим работу раньше срока или вернем 100% денег
Стоимость и сроки

Вершина параболы – это парабола, которая проходит через точки . Если точка принадлежит параболе, то и тоже принадлежит параболе, так как из:

Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:

Чтобы найти вершину параболы, необходимо знать формулу: .

Давайте посмотрим, как данная формула действует, допустим дано уравнение:

Тогда:

, , . Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:

, , .

Форма и характеристики параболы

Исследуем за каноническим уравнением форму и расположение параболы:

1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси . Ось – это ось, которая симметрична параболе.

2. Так как , тогда , откуда получается, что парабола расположена справа от оси .

3. При мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.

4. При увеличении значений переменной модуль тоже возрастает. Изобразим параболу на рисунке:

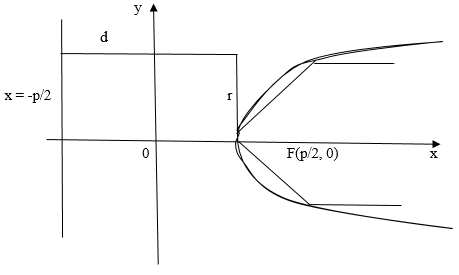
Возрастание параболы

Рис. 2

5. В полярной системе координат, у канонического уравнения параболы такой вид:

6. Уравнение , , , тоже описывают параболы:

Рис. 3

Оптическое свойство параболы

У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.

При положительном уравнении:

описывают параболу симметричную относительно с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).

Аналогично изложенному, уравнение и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно

и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .

Примеры решения

Когда нет времени!

Помощь в написании работы от 1 дня. Гарантируем сдачу работу к сроку без плагиата, только авторский текст. Оформление + сопровождеие в подарок!

Узнать стоимость Список услуг Задать вопрос

Задача

Найти координаты фокуса и составить уравнение директрисы параболы .

Решение

Сравнивая каноническое уравнение и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .

Ответ

координаты фокуса: , а уравнение директрисы параболы: .

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке ;

б) с фокусом в точке .

Решение

а). Так как фокус на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .

б). Фокус лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .

Ответ

а) каноническое уравнение параболы с фокусом в точке : ;

б) каноническое уравнение с фокусом в точке : .

Задача

Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной полный квадрат

= = = = = = .

Обозначим , . Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку , получим каноническое уравнение параболы .

Ветви этой параболы направлены вниз симметрично относительно оси , , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе .

Повернёмся к старым координатам при помощи замены , . Уравнение оси в новой системе , а в старой – уравнение оси параболы.

Уравнение директрисы в новой системе координат , а в старой .

В новой системе для фокуса , , а в старой системе , , то есть .

Ответ

Каноническое уравнение параболы – ;

вершина – ветви параболы направлены вниз;

, , – фокусное расстояние, а фокус находится в точке ;

уравнение оси ;

уравнение директрисы .

Источник