Какие свойства у параллелограмма

Определение.
Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Параллелограммы отличаются между собой как размером прилегающих сторон, так и углами, однако противоположные углы одинаковые.
Признаки параллелограмма
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
2. Четырехугольник имеет пару параллельных и равных сторон:
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Основные свойства параллелограмма
Квадрат, прямоугольник и ромб – есть параллелограммом.
1. Противоположные стороны параллелограмма имеют одинаковую длину:
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма одинаковые:
∠ABC = ∠CDA, ∠BCD = ∠DAB
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
6. Каждая диагональ делит параллелограмма на два равных треугольника
7. Две диагональ делят параллелограмм на две пары равных треугольников
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9. Точка пересечения диагоналей называется центром симметрии параллелограмма
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
a =
√d12 + d22 – 2d1d2·cosγ2 =
√d12 + d22 + 2d1d2·cosδ2
b =
√d12 + d22 + 2d1d2·cosγ2 =
√d12 + d22 – 2d1d2·cosδ2
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Определение.
Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.
Параллелограмм имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)
d1 = √a2 + b2 – 2ab·cosβ
d2 = √a2 + b2 + 2ab·cosβ
2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
d1 = √a2 + b2 + 2ab·cosα
d2 = √a2 + b2 – 2ab·cosα
3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:
d1 = √2a2 + 2b2 – d22
d2 = √2a2 + 2b2 – d12
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d1 = | 2S | = | 2S |
| d2·sinγ | d2·sinδ |
| d2 = | 2S | = | 2S |
| d1·sinγ | d1·sinδ |
Периметр параллелограмма
Определение.
Периметром параллелограмма называется сумма длин всех сторон параллелограмма.
Формулы определения длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали:
P = 2a + √2d12 + 2d22 – 4a2
P = 2b + √2d12 + 2d22 – 4b2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
Площадь параллелограмма
Определение.
Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.
Формулы определения площади параллелограмма:
1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:
S = a · ha
S = b · hb
2. Формула площади параллелограмма через две стороны и синус угла между ними:
S = ab sinα
S = ab sinβ
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
Источник
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a * h, где a — сторона, h — высота.
- S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
- S = 0,5 * (d1 * d2), где d1,d2 — две диагонали.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок математики в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
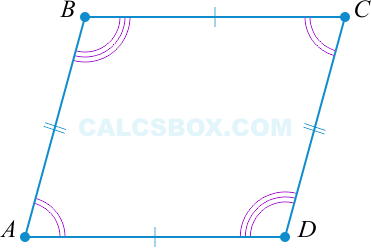
- Противоположные стороны параллелограмма ABCD равны: AB = DC, BC = AD.
- Противоположные углы параллелограмма ABCD равны:∠A = ∠C, ∠B = ∠D.
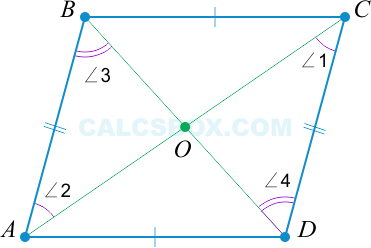
- Диагонали параллелограмма ABCD равны и точкой пересечения делятся пополам: BO = OD, AO = OC.
- Диагональ делит параллелограмм ABCD на два равных треугольника: △ABC = △CDA.
- Сумма углов в параллелограмме ABCD, прилежащих к одной стороне, равна 180 градусам: ∠A + ∠D = 180°.
- В параллелограмме ABCD накрест лежащие углы при диагонали равны: ∠BAC = ∠ACD, ∠BCA = ∠CAD.
- В параллелограмме ABCD сумма всех углов равна 360° градусам.
- Точка пересечения диагоналей является центром симметрии параллелограмма ABCD.
- В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 * (a2 + b2 ).
- Биссектриса отсекает от параллелограмма ABCD равнобедренный треугольник.
А сейчас докажем теорему, которая основана на первых двух свойствах.
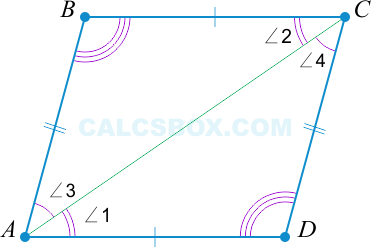
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- Как противоположные стороны параллелограмма: AB = CD
- Как внутренние накрест лежащие равны пары углов: ∠1 = ∠2, ∠3 = ∠4.
- Следовательно, треугольник AOB равен треугольнику COD, из чего следует:
- CO = OA
- BO = DO
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2, как внутренние накрест лежащие углы для параллельных прямых.
Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Рассмотрим треугольники ABC и ADC:
- AC — общая сторона;
- B = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и ADC равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы накрест лежащие при верхней и нижней сторонах и секущей диагонали, значит верхняя и нижняя стороны параллельны.
- ∠DAC = ∠BCA
Эти углы накрест лежащие при боковых сторонах и секущей диагонали. Поэтому боковые стороны четырёхугольника тоже параллельны. Значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащиз углов ∠1 = ∠2.
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все таки связано с параллельностью противоположных сторон.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Источник
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
Первым делом проведем диагональ ( AC ). Получаются два треугольника: ( ABC ) и ( ADC ).
Так как ( ABCD ) — параллелограмм, то справедливо следующее:
( AD || BC Rightarrow angle 1 = angle 2 ) как лежащие накрест.
( AB || CD Rightarrow angle3 = angle 4 ) как лежащие накрест.
Следовательно, ( triangle ABC = triangle ADC ) (по второму признаку: ( angle 1 = angle 2, angle 3 = angle 4 ) и ( AC ) — общая).
И, значит, ( triangle ABC = triangle ADC ), то ( AB = CD ) и ( AD = BC ).
2. Противоположные углы тождественны
Согласно доказательству свойства 1 мы знаем, что ( angle 1 = angle 2, angle 3 = angle 4 ). Таким образом сумма противоположных углов равна: ( angle 1 + angle 3 = angle 2 + angle 4 ). Учитывая, что ( triangle ABC = triangle ADC ) получаем ( angle A = angle C ), ( angle B = angle D ).
3. Диагонали разделены пополам точкой пересечения
По свойству 1 мы знаем, что противоположные стороны тождественны: ( AB = CD ). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что ( triangle AOB = triangle COD ) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, ( BO = OD ) (напротив углов ( angle 2 ) и ( angle 1 )) и ( AO = OC ) (напротив углов ( angle 3 ) и ( angle 4 ) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
( AB = CD ); ( AB || CD Rightarrow ABCD ) — параллелограмм.
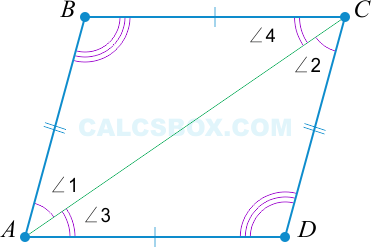
Рассмотрим подробнее. Почему ( AD || BC )?
( triangle ABC = triangle ADC ) по свойству 1: ( AB = CD ), ( angle 1 = angle 2 ) как накрест лежащие при параллельных ( AB ) и ( CD ) и секущей ( AC ).
Но если ( triangle ABC = triangle ADC ), то ( angle 3 = angle 4 ) (лежат напротив ( AD || BC ) (( angle 3 ) и ( angle 4 ) – накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
( AB = CD ), ( AD = BC Rightarrow ABCD ) — параллелограмм.
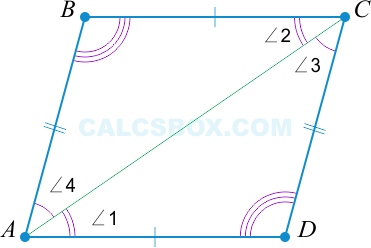
Рассмотрим данный признак. Еще раз проведем диагональ ( AC ).
По свойству 1 ( triangle ABC = triangle ACD ).
Из этого следует, что: ( angle 1 = angle 2 Rightarrow AD || BC ) и ( angle 3 = angle 4 Rightarrow AB || CD ), то есть ( ABCD ) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
( angle A = angle C ), ( angle B = angle D Rightarrow ABCD ) — параллелограмм.
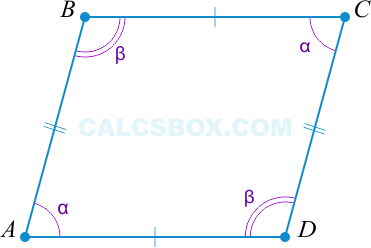
( 2 alpha + 2 beta = 360^{circ} ) (поскольку ( angle A = angle C ), ( angle B = angle D ) по условию).
Получается, ( alpha + beta = 180^{circ} ). Но ( alpha ) и ( beta ) являются внутренними односторонними при секущей ( AB ).
И то, что ( alpha + beta = 180^{circ} ) говорит и о том, что ( AD || BC ).
При этом ( alpha ) и ( beta ) — внутренние односторонние при секущей ( AB || CD ).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
( AO = OC ); ( BO = OD Rightarrow ) параллелограмм.
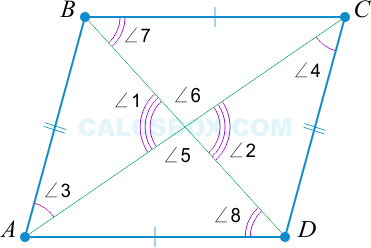
( BO = OD ); ( AO = OC ), ( angle 1 = angle 2 ) как вертикальные ( Rightarrow triangle AOB = triangle COD ), ( Rightarrow angle 3 = angle 4 ), и ( Rightarrow AB || CD ).
Аналогично ( BO = OD ); ( AO = OC ), ( angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8 ), и ( Rightarrow AD || BC ).
Четвертый признак верен.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Источник
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
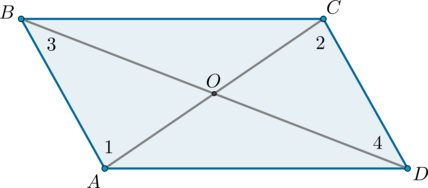
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
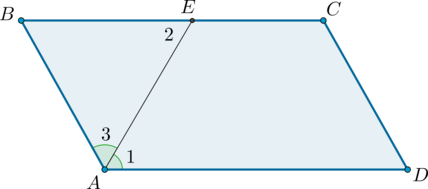
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
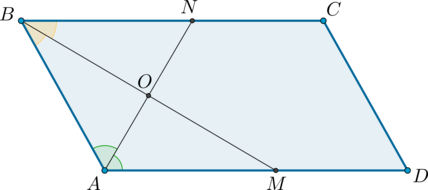
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ – (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
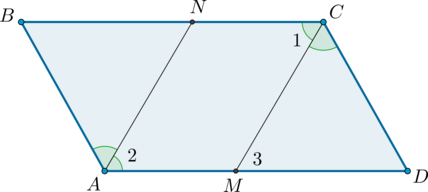
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Источник
Общие сведения о фигуре
Параллелограмм — это четырехугольник на плоскости, у которого присутствует равенство противоположных сторон, причем они лежат на параллельных прямых. Ромб, прямоугольник и квадрат — его частные случаи. Из него состоят более сложные объемные фигуры. Например, параллелепипед и куб. Высота параллелограмма — отрезок, который является перпендикуляром, проведенным к нижней стороне геометрической фигуры.
Всего можно провести четыре высоты. Две из них можно провести из вершин углов, которые лежат в параллелограмме и являются тупыми. Другие две высоты проводятся из острых углов (находятся вне фигуры). Углы делятся на шесть типов: острые, прямые, тупые, развернутые, выпуклые и полные.
Первый тип, градусная размерность которого меньше 90, является острым. Если значение равно 90, то он является прямым, и соответствует второму типу. В случае, когда выполняется условие 90 < a < 180, то угол считается тупым. При равенстве a = 180 — развернутый. При неравенстве 180 < a < 360 — выпуклый (смежный с ним угол является острым). Полным называется угол, градусная мера которого соответствует 360.
Для решения задач и выполнения расчетов необходимо знать следующие аспекты: свойства и признаки параллелограмма, а также уметь находить его углы, стороны, диагонали, периметр и площадь. Кроме того, следует знать не только основные соотношения фигуры, которая вписана в окружность, но и в случае, когда окружность находится внутри нее.
Информация о признаках
Признаки позволяют выяснить принадлежность фигуры к параллелограмму. Например, существует произвольный четырехугольник, и нужно выяснить, является ли он параллелограммом. Необходимо отметить, что при условии совпадения хотя бы одного из признаков, этот четырехугольник является им. Проверку следует производить, руководствуясь следующими утверждениями:
- Параллельность и равенство двух любых сторон.
- Равенство противолежащих сторон.
- Углы, которые являются противолежащими, равны.
- Точка пересечения диагоналей (центр симметрии) делит их на два равных отрезка.
- При выполнении равенства (d — диагонали): (d1)^2 + (d2)^2 = a 2 + b 2 + c 2 + d 2 .
Последний признак можно записать для упрощения расчетов следующим образом: sqr (d1) + sqr (d2) = 2 * (a 2 + b 2 ). Равенство можно упростить, поскольку противоположные стороны равны.
Основные свойства
Для решения задач и проектирования деталей необходимо знать основные свойства параллелограмма. Некоторые из них были получены при доказательстве и следствиях из теорем. К ним относятся следующие:
- Ромб, квадрат и прямоугольник — параллелограммы.
- Противоположные стороны одинаково равны и параллельны.
- Противолежащие углы равны.
- Суммарное значение градусной меры всех внутренних углов параллелограмма составляет 360.
- Сумма углов, прилегающих к одной из вершин, составляет 180 градусов.
- Диагональ делит фигуру на два треугольника, которые равны между собой по всем признакам.
- Две диагонали (одна — большая, а другая — меньшая) делят параллелограмм на две пары треугольников, которые равны между собой.
- Диагонали фигуры пересекаются, а точка пересечения делит их пополам (через нее можно провести среднюю линию, которая параллельна сторонам).
- Точка пересечения двух диагоналей является симметрией фигуры.
- Биссектрисы соседних углов пересекаются под углом в 90 градусов, а противоположных являются параллельными.
- sqr (d1) + sqr (d2) = 2 * ((a)^2 + (b)^2).
Однако для выполнения расчетов признаков и свойств параллелограмма недостаточно. В некоторых случаях требуется вычислить периметр и площадь фигуры. Соотношения используются не только в учебных заведениях, но и в научных исследованиях. Простым примером является нахождение площади поперечного сечения проводника. Это может понадобиться для дальнейшего вычисления электрического сопротивления.
Определение периметра
Периметром (P) любой фигуры является сумма длин всех ее сторон. Следовательно, для параллелограмма найти это значение является несложным. Базовая формула периметра параллелограмма имеет следующий вид: P = a + b + c + d = 2 * (a + b). Кроме того, существуют и другие соотношения для нахождения этой величины:
- Если известны одна из сторон и две диагонали.
- Нахождение периметра через сторону, высоту и синус угла.
В первом случае соотношение для стороны «a» записывается следующим образом: P = 2 * a + sqrt [2 * (d1 * d1 + d2 * d2 — 2 * a^(2))]. Для «b» запись изменяется таким образом: P = 2*b + sqrt [2 * (d1^(2) + d2^(2) — 2 * b^(2))].
Во втором случае, когда известна сторона «а», угол BAD и высота Ha, периметр записывается формулой вида: P = 2 * [a + Ha / sin (BAD)]. Для стороны «b», угла BAD и высоты Hb равенство принимает следующий вид: P = 2 * [b + Hb / sin (BAD)]. Если проанализировать последние два соотношения, то величины «Hb / sin (BAD)» и «Hа / sin (BAD)» являются стороной «b» и «a» соответственно.
Вычисление площади
Площадь параллелограмма (S) — это пространство, которое ограничено его сторонами, и равно произведению одной из сторон на высоту, проведенную к одноименному основанию. Базовая формула нахождения значения S является следующей: S = a * Ha = b * Hb. Кроме того, существует два способа нахождения ее значения, когда известны следующие величины:
- По сторонам и углу.
- Две диагонали и синус углов f или g между ними.
Можно записать соотношение следующим образом: S = a * b * sin (BAD) = a * b * sin (ABC). В последнем случае математическая запись площади имеет следующий вид: S = 0,5 * d1 * d2 * sin (f) = 0,5 * d1 * d2 * sin (g). Кроме того, существует формула Герона, которая позволяет вычислить площадь параллелограмма. Для этого необходимо вычислить полупериметр (p) треугольника со сторонами a, b и d: p = P / 2 = (a + b + d). Формула имеет вид: S = sqrt[p * (p — a) * (p — b) * (p — d)].
Соотношения сторон и диагоналей
В некоторых задачах необходимо определить неизвестные длины сторон или диагонали. Можно попытаться вывести соотношения, однако эта процедура занимает некоторое время. Следовательно, проще воспользоваться уже готовыми формулами. Стороны параллелограмма можно определить четырьмя основными выражениями. При этом следует знать следующие величины:
- Диагонали и угол.
- Другую сторону и диагонали.
- Высоту и значение синуса угла в градусах.
- Площадь и высоту.
В первом случае для вычисления длины стороны «а», следует воспользоваться следующей формулой: a = [sqrt (d1 *d1 + d2 * d2 — 2 * d1 * d2 * cos (f))] / 2 = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (g))] / 2. Значение стороны «b» вычисляется немного иначе: b = [sqrt (d1 * d1 + d2 * d2 + 2 * d1 * d2 * cos (f))] / 2 = [sqrt (sqr (d1) + sqr (d2) — 2 * d1 * d2 * cos (g))] / 2.
При известных значениях диагоналей и одной из сторон, соотношение имеет более простой вид, чем в первом случае: a = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * b 2 ))] / 2 и b = [sqrt (2 * (sqr (d1) + sqr (d2) — 2 * a 2 ))] / 2.
Когда известны высоты и угол BAD, можно найти стороны a и b: a = Hb / sin (BAD) и b = Ha / sin (BAD). Если известны площадь и высота, то соотношение принимает следующий вид: a = S / Ha и b = S / Hb.
Диагональ параллелограмма — отрезок, который соединяет его противоположные внутренние углы. Фигура имеет две диагонали, одна из которых длинная (d1), а другая является короткой (d2). Их можно найти, используя 4 соотношения. Это возможно в том случае, когда известны следующие данные:
- Стороны и косинус угла ABC.
- Cos (BAD) и стороны.
- Одну известную диагональ и стороны.
- Площадь, диагональ и угол между d1 и d2.
В первом случае можно воспользоваться следующими формулами (теорема косинусов): d1 = sqrt[a 2 + b 2 — 2 * a * b * cos (ABC)] и d2 = sqrt[a 2 + b 2 + 2 * a * b * cos (ABC)]. Во втором: d1 = sqrt[a 2 + b 2 + 2 * a * b * cos (BAD)] и d2 = sqrt[a 2 + b 2 — 2 * a * b * cos (BAD)].
Когда известны две стороны и одна из диагоналей, то можно воспользоваться третьим случаем: d1 = sqrt[2 * a 2 + 2 * b 2 — (d2)^2] и d2 = sqrt[2 * a 2 + 2 * b 2 — (d1)^2]. В последнем случае равенства для нахождения диагоналей имеют такой вид: d1 = 2 * S / [(d2) * sin (f)] = 2 * S / [(d2) * sin (g)] и d2 = 2 * S / [(d1) * sin (f)] = 2 * S / [(d1) * sin (g)].
Параллелограмм и окружность
Существуют определенный тип задач, в которых речь идет о параллелограмме и окружности. Всего бывает два варианта: вписанная и описанная окружности. Следует отметить, что не всегда это возможно. Существуют определенные условия, при которых возможны такие операции. Кроме того, следует обратить особое внимание на дополнительные свойства, которые появляются при комбинации данных фигур. Можно не только чередовать комбинации, но и использовать одновременно.
Для решения сложного типа задач и выполнения расчетов, в некоторых случаях рекомендуется применять вписанные и описанные окружности. Например, при проектировании деталей, необходимо полностью подогнать ее размеры, поскольку они должны быть правильной формы. При помощи окружности (вписанной или описанной) можно выявить ряд дефектов, которые могут привести к некорректной работе механизма.
Круг и прямоугольник
Главное условие: любой четырехугольник можно вписать в окружность, когда сумма его двух противоположных углов составляет 180 градусов. У параллелограмма есть одно свойство: сумма углов, которые прилегают к любой из вершин, составляет 180 градусов. Кроме того, сумма всех его углов составляет 360, а, следовательно, сумму противоположных углов составляет 360 — 180 = 180 (градусов).
Однако при попытке описать около него окружность ничего не выйдет, поскольку есть одно свойство: противоположные углы у него равны. Ими могут быть тупые и острые. Сумма градусной меры тупых углов будет больше 180, а острых — меньше. Когда противоположные углы будут равны 90, то значит их сумма составит 180. В этом случае нужно рассматривать частный случай — прямоугольник. Появляется очень важное свойство: диагонали прямоугольника пересекаются и точкой пересечения (центром окружности) делятся пополам, а также являются диаметрами окружности.
Для нахождения радиуса окружности, следует воспользоваться следующим соотношением (при условии, что известны стороны прямоугольника): R = [sqrt (a 2 + b 2 )] / 2 = d / 2. Величина «d» является диаметром.
Ромб и квадрат
В параллелограмм также можно вписать окружность. Однако для этого необходимо выполнение определенного условия. Оно заключается в следующем: суммы противолежащих сторон параллелограмма должны быть равны. Нужно отметить, что это выполняется только для ромба и квадрата.
Ромбом называется параллелограмм, стороны которого равны, а углы не равны 90 градусов. Квадрат — геометрическая фигура, у которой все стороны и углы равны. Из последнего определения можно найти значение градусной меры одного угла: 360 / 4 = 90. Последняя фигура является частным случаем ромба. Радиус окружности находится с помощью формулы: r = S / p = 0,5 * H. В этом соотношении переменные S, p и H — площадь, полупериметр и высота соответственно. Для нахождения S можно воспользоваться такими соотношениями:
- Известны длина стороны (а) и высота (H): S = a * H.
- Через диагонали d1 и d2: S = d1 * d2 / 2.
Полупериметром фигуры называется половина от значения ее периметра. Соотношение записывается таким образом: p = P / 2 = 4 * a.
Таким образом, знать основные свойства и признаки параллелограмма необходимо, поскольку от этого может зависеть не только качество сдачи экзаменов, решения задач, но и проектирование различных деталей.
Источник
