Какие свойства у радиуса

- KtoNaNovenkogo
- ЧАстые ВОпросы
- Вы здесь
16 января 2021
- Что такое радиус
- Радиус и диаметр
- Свойства радиуса
- Длина и площадь окружности
- Вместо заключения
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы продолжим знакомить вас с различными математическими терминами. И расскажем, что такое РАДИУС.
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
А именно:
Длина диаметра равна удвоенной длине радиуса.
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
- Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
Длина и площадь окружности через радиус
Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.
Длина окружности
Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.
Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:
Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.
Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.
Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.
Площадь окружности
Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:
Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Источник
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
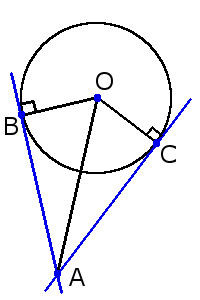
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
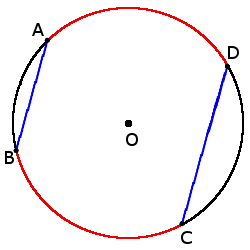
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
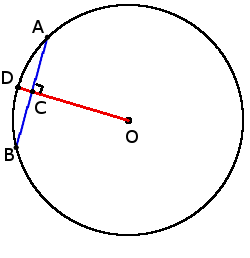
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
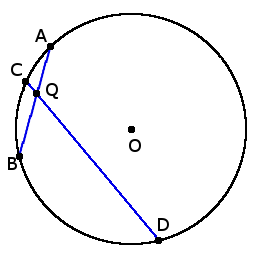
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
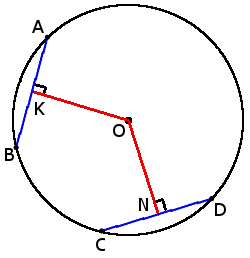
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
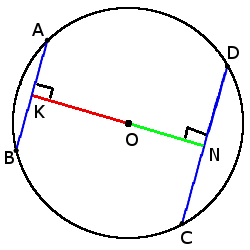
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
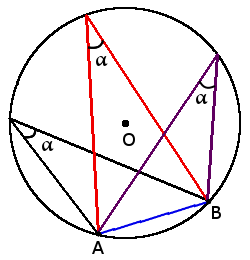
1. Все вписанные углы, которые опираются на одну дугу – равны.
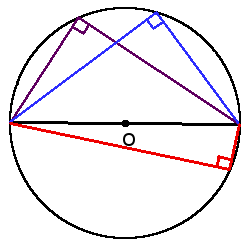
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
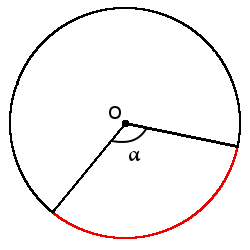
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
Что такое окружность?
Окружность — одна из самых важных кривых линий на плоскости, её можно начертить циркулем или даже натянутой верёвкой, если закрепить один из концов верёвки в данной точке. В любом случае расстояние от всех точек окружности до данной закреплённой точки будет одинаково. Эту точку называют центром окружности, а любой отрезок, который соединяет точку на окружности с её центром, называется радиусом. В переводе с латыни слово радиус означает “спица колеса”. Это не удивительно, ведь можно сказать, что окружность — это математическая модель колеса. Если две любые точки окружности соединить отрезком, то получится хорда. Хорда же в переводе с греческого языка означает “струна”. Если хорда проходит через центр окружности, то её называют диаметром и обычно обозначают буквой . Понятно, что длина диаметра окружности должна быть равна двум её радиусам, то есть . Давайте повторим ещё раз.
Определения.
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.
Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.
Хорда окружности — отрезок, соединяющий две любые её точки.
Диаметр окружности — это хорда, которая проходит через центр окружности.
Свойство диаметра.
Легко доказать, что диаметр окружности — это самая длинная её хорда. Да, и само слово диаметр в переводе означает “поперечник”. В технике измеряют диаметры колёс, труб, винтов и гвоздей и обозначают их таким значком .
Давайте сформулируем данное свойство диаметра как теорему.
Теорема.
Любая хорда окружности не превышает её диаметра.
Доказательство. Возьмём на окружности с центром в точке и радиусом любые две точки и . Если хорда проходит через центр окружности, то по определению она будет её диаметром и равна . Если же хорда не содержит центра окружности, то образуется треугольник . Тогда для него должно выполняться неравенство треугольника: . Значит, в любом случае хорда не может быть больше диаметра окружности. Что и требовалось доказать.
Полезно знать, что в геометрии диаметр можно определить не только для окружности или круга. Он есть у квадрата, треугольника, да и вообще у многих других геометрических фигур. А знаете, что называют диаметром фигуры? Так же, как и у окружности, диаметр фигуры — это самая длинная её хорда.
Определение.
Диаметр геометрической фигуры — это самое большое расстояние между любыми двумя точками этой фигуры.
Что такое круг?
Чем круг отличается от окружности? Каждый человек интуитивно понимает, что круг — это то, что находится “внутри ” окружности. Можно даже сказать, что для окружности круг — это её внутренняя область. Правда, работать с таким определением не очень удобно.
Как же можно удобно определить круг? Предположим, что один фермер выпустил пастись свою козу на луг, а чтобы она далеко не ушла, привязал её к колышку в точке с помощью верёвки длины . В течение дня коза выщипала траву везде, куда она смогла дотянуться. Как выглядит та часть луга, где паслась коза, и где теперь не стало травы?
Ясно, что коза не сможет отойти от колышка, к которому она привязана, дальше чем на длину своей верёвки. И она сможет дотянуться до любого места, которое ближе находится к этому колышку, чем длина её верёвки. Таким образом, коза выщиплет траву внутри круга с центром в точке и радиусом , равным длине её натянутой верёвки. Теперь мы с вами уже можем дать следующее определение.
Определение.
Круг — это множество всех точек плоскости, удалённых от данной точки не более, чем на длину данного отрезка.
Данная точка называется центром круга, а указанный отрезок — радиусом круга.
Круг с центром в точке и радиусом обозначают так: круг .
Разберём несколько примеров решения задач.
Пример 1. В окружности провели две хорды и , равные радиусу этой окружности. Найдите угол .
Решение. Отметим центр данной нам окружности и проведем радиусы в точки , и . Тогда треугольники и будут равносторонними. Значит, их углы и будут равны . Искомый угол равен их сумме, поэтому он будет равен .
Ответ: .
Пример 2. В окружность радиуса вписан квадрат. Найдите площадь этого квадрата.
Решение. Отметим центр данной нам окружности и проведем из него радиусы во все вершины квадрата .
Поскольку у квадрата все стороны равны, а радиусы окружности равны по определению, треугольники , , и будут равны по трём сторонам. Значит, равны все их углы при вершинах в точке . Сумма этих четырёх углов равна , поэтому каждый угол равен .
Запишем теорему Пифагора для треугольника : . Значит, сторона квадрата равна , а его площадь равна квадрату стороны. То есть, она равна .
Ответ: .
Пример 3. В окружность радиуса вписан равносторонний треугольник. Найдите расстояние от центра окружности до стороны этого треугольника.
Решение. Соединим центр окружности с вершинами равностороннего треугольника , который вписан в эту окружность. Поскольку все стороны треугольника равны, а радиусы окружности равны по определению, то равнобедренные треугольники , и будут равны по трём сторонам. Поэтому будут равны шесть углов при основаниях этих треугольников. Обозначим величину каждого из них через и запишем сумму всех углов треугольника : . Откуда .
Расстояние от точки до прямой линии — это длина перпендикуляра, опущенного из этой точки на данную прямую. Давайте опустим из точки перпендикуляр на сторону нашего треугольника и найдём его длину. Треугольник будет прямоугольным, причём его угол при вершине будет равен . Значит, по известному свойству катет против угла равен половине гипотенузы. То есть, .
Ответ: .
Источник

РА́ДИУС, -а, м.
1. Мат. Отрезок прямой, соединяющий какую-л. точку окружности или поверхности шара с центром, а также длина этого отрезка.
2. перен. Величина охвата, сфера действия, распространения чего-л. (по отношению к какому-л. центру). Белый показал Макарову по карте расположение береговых батарей, радиус их действия. Степанов, Порт-Артур.
[Лат. radius]
Источник (печатная версия): Словарь русского языка: В 4-х
т. / РАН,
Ин-т лингвистич.
исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.;
Полиграфресурсы,
1999;
(электронная версия): Фундаментальная
электронная
библиотека
- Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра.
Источник: Википедия
РА’ДИУС, а, м. [латин. radius — луч, спица]. 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен. Величина охвата чего-н., сфера распространения чего-н. (по отношению к какому-н. центру; книжн.). Р. действия. 3. Лучевая кость предплечья (анат.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940);
(электронная версия): Фундаментальная
электронная
библиотека
ра́диус
1. геометр. отрезок прямой, соединяющий центр окружности (шара) с точкой на этой окружности (на шаре), а также длина этого отрезка
2. перен. охват, область распространения, действия чего-либо
3. трансп. участок пути, маршрут транспорта, связывающий центр города с периферией
Источник: Викисловарь
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: зародиться — это что-то нейтральное, положительное или отрицательное?
Ассоциации к слову «радиус»
Синонимы к слову «радиус»
Предложения со словом «радиус»
- Тактическая авиация военно-морского флота – это огневая мощь, торпедное вооружение и разведка – причём с гораздо большим радиусом действия по сравнению с боевыми кораблями.
- В перенапряжённых мышцах ощущалась непроизвольная дрожь, в суставах чувствовалась ломота – то была неизбежная цена удара, обезвредившего всех противников в радиусе нескольких километров.
- Как только понадобится – в радиусе ста метров ничего достойного не отыщешь.
- (все предложения)
Цитаты из русской классики со словом «радиус»
- А так как она не нуль — это мы знаем, — то, следовательно, Вселенная — конечна, она сферической формы, и квадрат вселенского радиуса у2 равен средней плотности, умноженной на…
- И теперь на столе перед ним стоял небольшой прибор, с несколькими трубками, расположенными по радиусам.
- Посредине — площадь, от которой радиусами разбегаются во все стороны улицы, или, как он мысленно называл их, роты.
- (все
цитаты из русской классики)
Понятия со словом «радиус»
Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или сфере), а также длина этого отрезка. Радиус составляет половину диаметра.
Гравитацио́нный ра́диус (или ра́диус Шва́рцшильда) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы, на которой находился бы горизонт событий, создаваемый этой массой (с точки зрения ОТО), если бы она была распределена сферически-симметрично, была бы неподвижной (в частности, не вращалась, но радиальные движения допустимы), и целиком лежала бы внутри этой сферы. Введен в научный обиход немецким ученым Карлом Шварцшильдом в…
Радиус атома — расстояние между атомным ядром и самой дальней из стабильных орбит электронов в электронной оболочке этого атома.
Гидродинамический радиус (англ. hydrodynamic radius или Stokes radius, Stokes-Einstein radius) — размер объекта, который рассчитывается, исходя из предположения о его сферической форме, по величине коэффициента диффузии в жидкости.
Вандерваальсовы радиусы определяют эффективные размеры атомов благородных газов. Кроме того, вандерваальсовыми радиусами считают половину межъядерного расстояния между ближайшими одноимёнными атомами, не связанными между собой химической связью и принадлежащими разным молекулам (например, в молекулярных кристаллах). При сближении атомов на расстояние, меньшее суммы их вандерваальсовых радиусов, возникает сильное межатомное отталкивание. Поэтому вандерваальсовы радиусы характеризуют минимальные допустимые…
Подробнее: Радиус Ван-дер-Ваальса
- (все понятия)
Источник
