Какие свойства у ромба

3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сумма внутренних углов любого четырехугольника равна (360^circ).
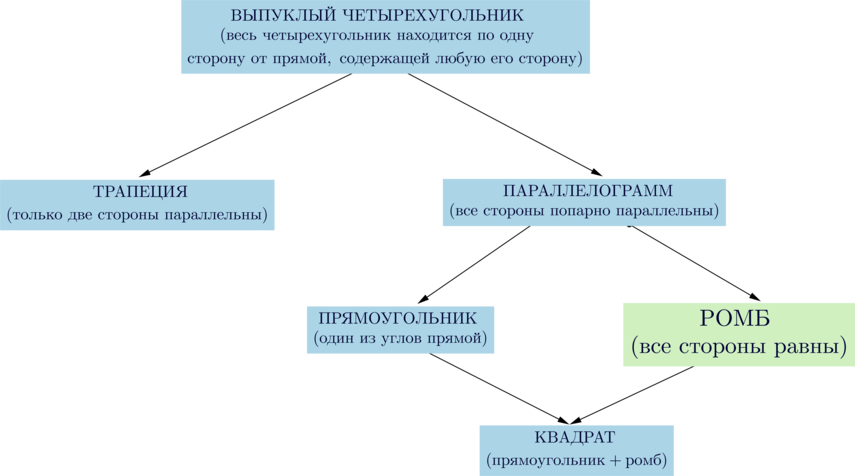
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
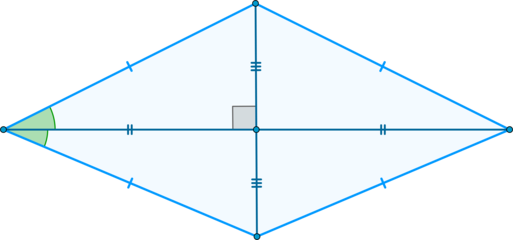
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
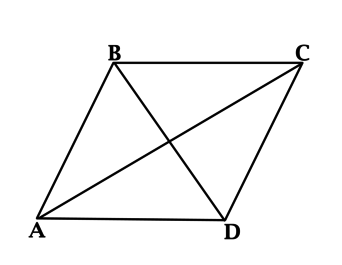
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} – angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
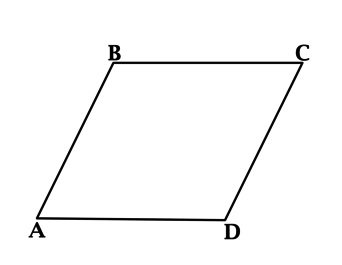
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
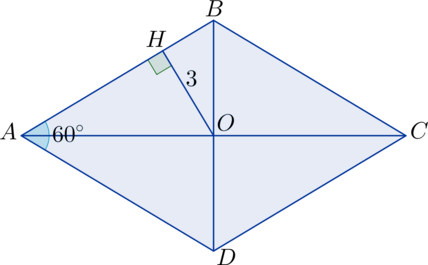
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
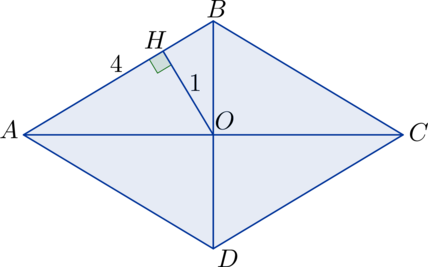
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 8).
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
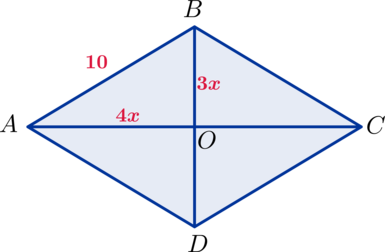
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
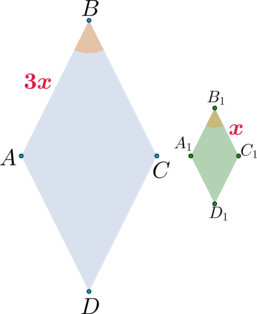
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.
Источник
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Источник
Ромб, его свойства и признаки.
Рассмотрим ещё два вида параллелограмма.
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
Поскольку ромб является параллелограммом, то он обладает теми же свойствами, что и параллелограмм, т.е.: у ромба противолежащие углы равны (стороны у него и так все равны, поэтому в этом свойстве мы опускаем равенство противолежащих сторон); диагонали ромба пересекаются и точкой пересечения делятся пополам. Кроме того, ромб обладает ещё и своими, особенными свойствами. Рассмотрим их.
ТЕОРЕМА. У ромба диагонали взаимно перпендикулярны.

Дано: – ромб
и диагонали.
Доказать: .
Доказательство.
Для того, чтобы доказать, что , нам нужно доказать, что хотя бы один из четырёх углов, которые получаются при пересечении диагоналей, равен .
1. Рассмотрим и .
по III признаку равенства треугольников. Следовательно, все соответствующие углы у этих треугольников равны, т.е. .
2. и – смежные, значит, по свойству смежных углов
, как, впрочем, и остальные углы (мы знаем, что если угол прямой, то смежный с ним угол также прямой).
3. Итак, прямые и при пересечении образуют прямой угол, значит, эти прямые перпендикулярны, т.е. , ч.т.д.
ТЕОРЕМА. У ромба диагонали являются биссектрисами углов.

Дано: – ромб
и диагонали.
Доказать: – биссектриса и
– биссектриса и .
Доказательство.
Для того, чтобы доказать, что и являются биссектрисами углов, нам нужно доказать, что они делят эти углы пополам.
1. Рассмотрим и .
по III признаку равенства треугольников. Следовательно, все соответствующие углы у этих треугольников равны, т.е. и . Следовательно, – биссектриса и .
2. Рассмотрим и .
по III признаку равенства треугольников. Следовательно, все соответствующие углы у этих треугольников равны, т.е. и . Следовательно, – биссектриса и , ч.т.д.
ТЕОРЕМА. У ромба высоты равны.

Дано: – ромб
и – высоты.
Доказать:
Доказательство.
Рассмотрим и .
по признаку равенства прямоугольных треугольников (по гипотенузе и острому углу). Значит, все соответствующие стороны у этих треугольников равны, т.е. , ч.т.д.
Итак, ромб обладает следующими свойствами:
У ромба диагонали пересекаются и точкой пересечения делятся пополам.
У ромба диагонали взаимно перпендикулярны.
У ромба диагонали являются биссектрисами его углов.
У ромба противоположные углы равны.
У ромба высоты равны.
Теперь определим признаки ромба.
ТЕОРЕМА (I признак ромба). Если у параллелограмма две смежные стороны равны, то такой параллелограмм является ромбом.

Дано: – параллелограмм
Доказать: – ромб.
Доказательство.
Так как – параллелограмм, то у него противолежащие стороны равны.
– ромб (по определению), ч.т.д.
ТЕОРЕМА (II признак ромба). Если у параллелограмма диагонали взаимно перпендикулярны, то такой параллелограмм является ромбом.
Дано: – параллелограмм
Доказать: – ромб.
Доказательство.
Рассмотрим .
по свойству диагоналей параллелограмма, значит, – медиана (по опред-нию).
– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку ромба, параллелограмм является ромбом, ч.т.д.
ТЕОРЕМА (III признак ромба). Если у параллелограмма диагональ является биссектрисой его угла, то этот параллелограмм является ромбом.
Дано: – параллелограмм
– диагональ
– биссектриса
Доказать: – ромб.
Доказательство.
Так как – биссектриса , то .
по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку ромба, параллелограмм является ромбом, ч.т.д.
ТЕОРЕМА (IV признак ромба). Если у параллелограмма высоты равны, то такой параллелограмм является ромбом.

Дано: – параллелограмм
и – высоты
Доказать: – ромб.
Доказательство.
Рассмотрим и .
по признаку равенства прямоугольных треугольников (по катету и острому углу). Значит, все соответствующие стороны у этих треугольников равны, т.е. . По I признаку ромба, параллелограмм является ромбом, ч.т.д.
ТЕОРЕМА (V признак ромба). Если в четырёхугольнике все стороны равны, то он является ромбом.

Дано: – четырёхугольник
Доказать: – ромб.
Доказательство.
Проведём диагональ и рассмотрим и .
по III признаку равенства треугольников, следовательно, все соответствующие углы у этих треугольников равны, т.е. и . Значит, по признаку параллельности прямых, и , следовательно, – параллелограмм, у которого все стороны равны, значит, он является ромбом, ч.т.д.
Итак, признаки ромба:
Если у параллелограмма две смежные стороны равны, то такой параллелограмм является ромбом.
Если у параллелограмма диагонали взаимно перпендикулярны, то такой параллелограмм является ромбом.
Если у параллелограмма диагональ является биссектрисой его угла, то этот параллелограмм является ромбом.
Если у параллелограмма высоты равны, то такой параллелограмм является ромбом.
Если в четырёхугольнике все стороны равны, то он является ромбом.
Сторона ромба равна см. Найдите периметр ромба.
Вычислите периметр ромба, один из углов которого равен , а длина меньшей диагонали равна см.
Найдите все углы ромба, если его сторона равна диагонали.
Диагонали ромба пересекаются в точке . Найдите углы треугольника , если .
Из вершины ромба проведены перпендикуляры и к прямым и . Докажите, что луч является биссектрисой .
Сторона ромба равна см, . Из вершины проведены высоты и к сторонам и соответственно. Найдите расстояния . Докажите, что треугольник равносторонний.
Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
Периметр ромба равен см, расстояние между противолежащими сторонами равно см. Найдите углы ромба.
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен .
Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на меньше другого.
Углы, образуемые стороной ромба с его диагоналями, относятся как . Найдите углы ромба.
Докажите, что точка пересечения диагоналей ромба равноудалена от его сторон.
Докажите, что параллелограмм, у которого две смежные стороны равны, является ромбом.
Докажите, что если каждая диагональ четырёхугольника делит пополам два его угла, то этот четырёхугольник является ромбом.
Через точку пересечения диагоналей ромба проведены перпендикуляры к его сторонам. Докажите, что точки пересечения этих перпендикуляров со сторонами ромба являются вершинами прямоугольника.
Точки – середины сторон ромба . Докажите, что четырёхугольник является прямоугольником.
В ромбе точки – середины его сторон. Докажите, что точки лежат на одной прямой с серединами отрезков: а) и б) и .
В параллелограмме биссектрисы углов и пересекают стороны параллелограмма и в точках и соответственно. Докажите, что четырёхугольник – ромб.
В ромбе биссектриса угла пересекает сторону и диагональ соответственно в точках и . Найдите угол , если .
В ромбе угол равен . Докажите, что если один из углов треугольника равен , то и остальные его углы тоже равны по .

Расстояние от точки пересечения диагоналей ромба до прямой равно м. Найдите длину высоты ромба, проведённой к стороне .
В ромбе перпендикуляр, проведённый из вершины тупого угла к стороне ромба, делит эту сторону пополам. Найдите углы ромба.
Докажите, что четырёхугольник, вершины которого находятся в серединах сторон прямоугольника, является ромбом.
Периметр ромба равен см. Найдите сторону ромба.
В ромбе с острым углом , равным , проведена диагональ . Найдите угол .
В ромбе с тупым углом диагонали пересекаются в точке . Один из углов треугольника равен . Найдите остальные углы этого треугольника и угол .
В ромбе . Диагонали пересекаются в точке . Найдите углы треугольника .
В ромбе – точка пересечения диагоналей, – перпендикуляры, опущенные на стороны соответственно. Докажите, что , и найдите сумму углов и .
В ромбе диагонали пересекаются в точке . На сторонах взяты точки соответственно, . Докажите, что , и найдите сумму углов и .
В ромбе угол тупой. На стороне взята точка . Прямые и пересекаются в точке . Найдите угол .
В ромбе угол острый. Отрезок является перпендикуляром к прямой – точка пересечения диагоналей, а – общая точка прямых и . Найдите .
Два ромба имеют общую точку пересечения диагоналей, причём, меньшие диагонали этих ромбов взаимно перпендикулярны. Докажите, что прямая, проходящая через точку пересечения диагоналей и середину стороны одного ромба, перпендикулярна стороне другого.
Два ромба и имеют общую вершину острого угла, причём, , а лучи и пересекаются в точке – точка пересечения диагоналей ромба – биссектриса треугольника . Докажите, что .
На сторонах ромба взяты точки соответственно. Каждая из прямых параллельная одной из осей симметрии ромба. Диагональ пересекает отрезок в точке , о отрезок – в точке . Докажите, что диагонали четырёхугольника равны, и определите вид выпуклого четырёхугольника .
Найдите величину большего угла ромба, если его сторона равна одной из его диагоналей.
Точка лежит на стороне параллелограмма так, что – биссектриса угла . Прямая параллельна и пересекает сторону в точке . Найдите величину угла между прямыми и .

Отрезки – биссектрисы углов параллелограмма . Отрезки и пересекаются в точке , а отрезки и – в точке , при этом . Найдите длину отрезка .
В ромбе диагонали и пересекаются в точке . Найдите углы треугольника .

Диагонали и ромба пересекаются в точке . Найдите углы треугольника .
Диагонали ромба пересекаются в точке . Найдите углы треугольника , если .
На стороне параллелограмма взята точка так, что .
Докажите, что – биссектриса угла .
Найдите периметр параллелограмма, если .
В параллелограмме проведена биссектриса угла , которая пересекает сторону в точке .
Докажите, что треугольник равнобедренный.
Найдите сторону , если , а периметр параллелограмма равен .
Один из углов ромба равен . Определите остальные углы.
В ромбе проведена диагональ . Определите вид треугольника и найдите его углы, если .
В ромбе , диагонали пересекаются в точке . Найдите углы треугольника .
Определите вид четырёхугольника и найдите его периметр, если .

Диагонали ромба пересекаются в точке . Найдите углы и , если .
Известно, что четырёхугольник является ромбом. Докажите, что .
Один из углов ромба на больше другого. Найдите углы треугольника , если – точка пересечения диагоналей.
На рисунке – равнобедренный, точки и – середины его боковых сторон, – точка на основании, . Определите вид четырёхугольника и найдите его периметр, если см.
В ромбе . Найдите углы треугольника .

Сторона ромба образует с его диагоналями углы, разность которых равна . Определите углы ромба.
Углы, образуемые стороной ромба с его диагоналями, относятся как . Определите углы ромба.
Углы, образуемые стороной ромба с его диагоналями, относятся как . Определите углы ромба.
Найдите острый угол ромба , если высота , проведённая из вершины тупого угла, делит сторону пополам.

На каждой стороне ромба отложены, как показано на рисунке, равные отрезки . Определите вид четырёхугольника . Ответ объясните.
В ромбе из вершины тупого угла проведена высота к стороне , а из вершины тупого угла проведена высота к стороне . Определите взаимное расположение прямых и .

В равнобедренный треугольник вписан ромб , имеющий с ним общий угол. Найдите периметр ромба, если боковая сторона треугольника равна см.

В ромбе биссектриса угла делит сторону ромба пополам. Найдите тупой угол ромба.
Один из углов ромба равен . Найдите угол между меньшей диагональю ромба и его стороной.
В ромбе диагонали пересекаются в точке . Найдите углы ромба, если разность и равна .
В ромбе диагонали пересекаются в точке . Найдите углы ромба, если .
Периметр ромба равен , один из его углов . Найдите меньшую диагональ ромба.
Сторона ромба равна см, а острый угол равен . Из вершины тупого угла проведена высота, которая делит сторону на два отрезка. Найдите длины этих отрезков.
Диагональ ромба, лежащая напротив угла , равна . Найдите периметр ромба.
8
Источник
