Какие свойства у трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции – параллельные стороны
Боковые стороны – две другие стороны
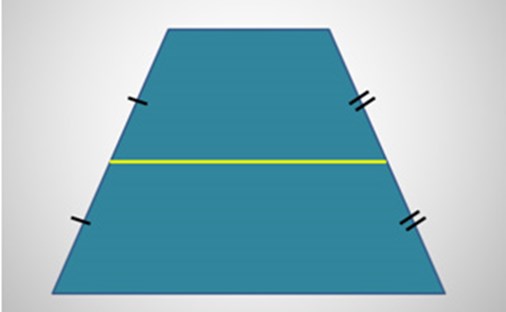
Средняя линия – отрезок, соединяющий середины боковых сторон.

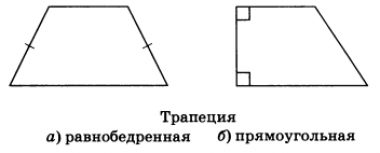
Виды трапеций:

Равнобедренная трапеция – трапеция, у которой боковые стороны равны
Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

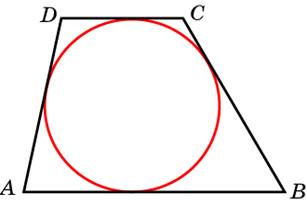
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:

d12 + d22 = 2ab + c2 + d2

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m – b

b = 2m – a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a – h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a – c·cos α – d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d1d2	=	sin δ ·	d1d2
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d1d2	=	sin δ ·	d1d2
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d1 = √a2 + d2 – 2ad·cos β

d2 = √a2 + c2 – 2ac·cos β

2. Формулы диагоналей через четыре стороны:

d1 =	√	d 2 + ab –	a(d 2 – c2)
			a – b

d2 =	√	c2 + ab –	a(c2 – d 2)
			a – b

3. Формула длины диагоналей через высоту:

d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2

d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2

4. Формулы длины диагонали через сумму квадратов диагоналей:

d1 = √c2 + d 2 + 2ab – d22

d2 = √c2 + d 2 + 2ab – d12

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d1d2	· sin γ	=	d1d2	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c2 –	(	(a – b)2 + c2 – d 2	)	2
	2				2(a – b)

5. Формула Герона для трапеции

S =	a + b	√(p – a)(p – b)(p – a – c)(p – a – d)
	\|a – b\|

где

p =	a + b + c + d	– полупериметр трапеции.
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p – a)(p – c)(p – d1)

где

a – большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Источник

Привет!

Перед тобой лучший гид по трапеции! Только то, что нужно. Без воды.

Основные определения, формулы и свойства.

Помни о своей цели!

Тебе нужно подготовиться к ЕГЭ по математике так, чтобы поступить в ВУЗ мечты! Будь уверен!

Приступим!

Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).

Сумма углов при каждой боковой стороне трапеции равна 180°
( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ )

Средняя линия трапеции (( displaystyle MN)) – отрезок, соединяющий середины боковых сторон:

( displaystyle AM=MB, CN=ND).

Средняя линия параллельна основаниям: ( displaystyle MNparallel BCparallel AD).
Длина средней линии трапеции равна полусумме длин оснований: ( displaystyle MN=frac{BC+AD}{2}).

Диагонали любой трапеции пересекаются в точке О.

Треугольники, образованные основаниями трапеции и отрезками диагоналей
(( displaystyle BOC) и ( displaystyle AOD)) подобны по двум углам с коэффициентом подобия равным отношению оснований: ( displaystyle k=frac{BC}{AD}).
Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: ( displaystyle {{S}_{Delta AOB}}={{S}_{Delta COD}}).

Равнобедренная (равнобокая) трапеция – это трапеция, у которой боковые стороны равны:

( displaystyle AB=CD).

Свойства равнобедренной трапеции:

диагонали равны: ( displaystyle AC=BD);
углы при основании равны: ( displaystyle angle A=angle D,text{ }angle B=angle C);
сумма противолежащих углов равна ( displaystyle 180{}^circ ): ( displaystyle angle A+angle C=angle B+angle D=180{}^circ ).

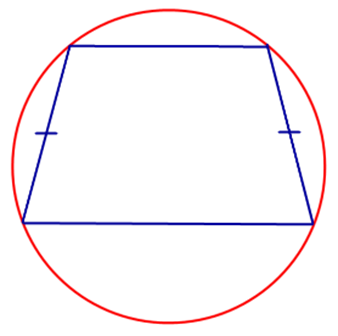
Если трапецию можно вписать в окружность, то она – равнобокая.
Стороны и диагональ равнобокой трапеции связаны соотношением: ( displaystyle A{{C}^{2}}=B{{D}^{2}}=ADcdot BC+A{{B}^{2}}).

Площадь трапеции равна полусумме оснований, умноженной на высоту: ( displaystyle {{S}_{ABCD}}=frac{BC+AD}{2}cdot h).

НАЧАЛЬНЫЙ УРОВЕНЬ

Что такое трапеция?

Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.

Вот, смотри:

Оказывается, трапеция (как и треугольник) бывает равнобедренная.

Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой).

И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ?

А вот и нет. Тогда это получится не трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма)

НЕ ПРОПУСТИ!

Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.

На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.

Регистрируйся здесь и приходи!

Свойства трапеции

Итак, что ты должен знать о свойствах трапеции…

Сумма углов при каждой боковой стороне трапеции равна 180°.
(у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))

Почему так?

Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB).

Поэтому ( displaystyle angle 1+angle 2=180{}^circ ).

И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).

Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.

Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:

Снова порассуждаем об углах:

Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).

А теперь рассмотрим сразу 2 диагонали и 4 угла:

( displaystyle angle 1=angle 2)

( displaystyle angle 3=angle 4)

Что из этого может следовать?

Очень важный факт:

Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).

Средняя линия трапеции

Для начала – что же такое средняя линия трапеции?

Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции.

Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:

( displaystyle m=frac{a+b}{2}), то есть:

Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований.

А ещё:

Средняя линия трапеции параллельна ее основаниям.

Трапеция, вписанная в окружность

Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:

Если трапецию можно вписать в окружность, то она – равнобокая.

Доказывать это мы не будем (здесь, во всяком случае), а вот запомнить хорошо бы – пригодится!

Подведём итог – он короткий.
Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.

Так что, если у тебя в задаче трапеция, – используй параллельность и всё получится!

НРАВИТСЯ УЧЕБНИК?

Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.

Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.

От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.

Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны называются основаниями, а непараллельные – боковыми сторонами.

Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой).

Почему? ( displaystyle AD) и ( displaystyle BC) – параллельны, а ( displaystyle AB) и ( displaystyle CD) – секущие, поэтому:

( angle 1+angle 2=180{}^circ );
( angle 3+angle 4=180{}^circ ).

Треугольники ( displaystyle BOC) и ( displaystyle AOD) подобны по двум углам.
(( displaystyle angle 1=angle 2) и ( displaystyle angle 3=angle 4) – как накрест лежащие)

Коэффициент подобия треугольников ( displaystyle BOC) и ( displaystyle AOD) равен отношению оснований:

( K=frac{a}{b})

Зарегистрируйся один раз и ты откроешь все 100 статей учебника

А также получишь доступ к видеоурокам и другим бесплатным материалам курса “Подготовка к ЕГЭ с репетитором”

* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент

Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

А теперь формула:

А вот и само третье свойство трапеции:

Средняя линия трапеции равна полусумме оснований и параллельна им.

А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!

Итак, проведём ( displaystyle CEparallel AB). Тогда четырехугольник ( displaystyle ABCE) – параллелограмм.

Возьмём середину ( displaystyle M) стороны ( displaystyle AB) и середину ( displaystyle K) стороны ( displaystyle CE).

Оба: ( displaystyle MBCK) и ( displaystyle AMKE) – снова параллелограммы (( displaystyle MBparallel CK) и ( displaystyle MB=CK); ( displaystyle AMparallel KE) и ( displaystyle AM=KE)).

Ну вот, значит ( displaystyle MKparallel AD), да ещё ( displaystyle MK=BC=a).

Поедем дальше.

Проведём ( displaystyle KN) – среднюю линию в ( displaystyle Delta ECD).

Знаем, что ( displaystyle KNparallel ED) и ( KN=frac{1}{2}ED)

Что же из всего этого следует?

( displaystyle MNparallel AD) (так как через точку ( displaystyle K) можно провести лишь одну прямую параллельную ( displaystyle AD), поэтому ( displaystyle MK) и ( displaystyle KN) – одна прямая ( displaystyle MN))
( displaystyle MN=MK+KN=a+frac{b-a}{2})
( displaystyle MN=frac{a+b}{2})

Вот и доказали!

Если трапеция вписана в окружность, то она равнобокая.

Почему?

Подробнее смотри в теме «Вписанный четырехугольник», а тут – двумя строчками:

( angle 1+angle 2=180{}^circ ) (трапеция же!)

( angle 3+angle 2=180{}^circ ) (вписанный четырехугольник)

( Rightarrow angle 1=angle 3). Ну, и так же ( angle 2=angle 4).

В любой трапеции следующие четыре точки лежат на одной прямой:

( displaystyle E) – точка пересечения продолжений боковых сторон;
( displaystyle F) и ( displaystyle H) – середины оснований;
( displaystyle G) – точка пересечения диагоналей.

Эту теорему доказывать не будем – не пугайся.

Заметим только, что ВЕРНО и ОБРАТНОЕ:

Если в каком-нибудь четырехугольнике какие-нибудь три из перечисленных четырёх точек окажутся на одной прямой, то четырёхугольник этот – ТРАПЕЦИЯ.

Биссектрисы углов при боковой стороне трапеции перпендикулярны.

( left{ begin{array}{l}angle 1+angle 2+angle 3+angle 4=180{}^circ -так, как, трапеция\angle 1=angle 2\angle 3=angle 4 -так, как, биссектрисаend{array} right.Rightarrow 2cdot angle 2+2cdot angle 3=180{}^circ Rightarrow )

( angle 2+angle 3=90{}^circ Rightarrow angle AEB =90{}^circ )

Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд. Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.

В трапеции с перпендикулярными диагоналями ( FH=frac{AD+BC}{2})

Давай докажем! Это уже целая задача, которая вполне может попасться прямо на ЕГЭ!

Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные. Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.

Проведём ( displaystyle BKparallel AC) и ( displaystyle BLparallel FH).

Обозначим ( displaystyle BC=text{ }a); ( displaystyle AD=b).

Тогда:

( displaystyle Delta KBD) – прямоугольный
( begin{array}{l}left{ begin{array}{l}LD=frac{b}{2}+frac{a}{2}=frac{a+b}{2}\LK=a+frac{b}{2}-frac{a}{2}=frac{a+b}{2}end{array} right.Rightarrow BL-медиана~в~ Delta KBD.\end{array})

Значит, ( BL=frac{KD}{2}) (медиана, проведенная к гипотенузе, равна её половине).

То есть ( BL=frac{a+b}{2}).

Но ведь ( displaystyle FH=BL) (так как ( displaystyle BFHL) – параллелограмм)( Rightarrow ) ( FH=frac{a+b}{2}).

P.S. Последний бесценный совет!

Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.

Это статистика. Но и это не главное.

Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…

Но думай сам…

Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.

Первое, тебе нужно набить руку, решая задачи

На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.

Второе, заниматься по системе – иначе у тебя уйдет много времени и ты, что-нибудь пропустишь.

И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.

Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.

Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.

Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.

Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.

Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:

Источник

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k2.
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 1800: α + β = 1800 и γ + δ = 1800.
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 900 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 1800 – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*SАМЕ.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 1800 – МЕТ = 1800 – КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной: