Какие углы называются перпендикулярными каким свойством они обладают
Какие прямые называются перпендикулярными
Определение
Если пара пересекающихся прямых составляют угол в 90 градусов, то такие линии имеют название перпендикулярные.
Схематично перпендикулярные линии АС и ВD будут выглядеть таким образом:

Обозначение перпендикулярных прямых в геометрии имеет такой вид:
(ACperp BD)
Признак перпендикулярности, какие условия необходимы, чему равен угол
Угол между парой пересекающихся линий в пространстве может быть прямым. В таком случае рассматриваемые прямые будут перпендикулярными.
Если угол, который образовали две скрещивающиеся прямые, будет прямым, то такие линии также будут перпендикулярными. Исходя из данного утверждения, можно заключить, что перпендикуляры на плоскости являются пересекающимися, а перпендикулярные линии в пространстве могут быть пересекающимися и скрещивающимися. Таким образом, выражения «прямые а и b перпендикулярны» и «прямые b и а перпендикулярны» можно считать равноправными. Согласно этому определению, сформулировано понятие взаимно перпендикулярных прямых.
При определении перпендикулярности линий необходимо учитывать их характеристики, которые имеют большое значение в решении задач. Основные признаки:
- Через какую-то точку А возможно начертить единственную перпендикулярную линию основному отрезку, остальные линии будут являться наклонными и могут скрещиваться.
- Несколько перпендикуляров ни при каких условиях не будут между собой пересекаться.
К примеру, можно изобразить на рисунке прямую PQ и пару линий, которые перпендикулярны ей: АА и ВВ. Необходимо доказать, что заданные прямые не имеют точек пересечения.

Подтверждение целесообразно строить с помощью метода «от обратного». Предположив, что прямые будут пересекаться в точке М1, получим какую-то точку М в другой полуплоскости, относительно прямой PQ. Таким образом, две точки пересекают две прямые, что не соответствует аксиоме. Поэтому предположение является неверным, а линии АА и ВВ не имеют точек пересечения:
Можно сделать вывод о том, что пара прямых, перпендикулярных третьей, не обладают общими точками пересечения.
Теорема о перпендикулярных прямых, как доказать
Задачи на перпендикулярные прямые, как правило, решают с учетом свойств этих линий. Доказательством перпендикулярности прямых является прямой угол, который они составляют. В том случае, когда требуется определить их перпендикулярность при известных уравнениях прямоугольной системы координат, следует применить необходимое и достаточное условие перпендикулярности линий.
Теорема 1
Теорема 1
Для того чтобы прямые a и b являлись перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Подтверждением данной теоремы является определение направляющего вектора прямой и перпендикулярности линий.
Допустим, что имеется прямоугольная декартовая система координат Оху, на которой заданы уравнения для прямой на плоскости, определяющие линии а и b. Направляющие векторы, характерные для данных прямых а и b, можно обозначить, как:
(vec{a}) и (vec{b})
Согласно формуле прямых а и b, необходимым и достаточным условием является перпендикулярность векторов (vec{a}) и (vec{b}.)
Данное утверждение справедливо в том случае, когда скалярное произведение векторов:
(vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) не равно нулю, а запись обладает таким видом:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)
Таким образом, необходимое и достаточное условие перпендикулярности линий а и b, которые расположены в прямоугольной системе координат Оху на плоскости, представляет собой следующее выражение:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)
где (vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) являются направляющими векторами линий а и b.
Данную теорему целесообразно использовать в том случае, когда требуется определить координаты направляющих векторов, либо, когда известны канонические или параметрические уравнения прямых на плоскости заданных линий а и b.
Примечание
Необходимое и достаточное условие перпендикулярности прямых а и b можно применять в случае трехмерного пространства.
В данном отношении запись будет иметь такой вид:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}+ a_{z}*b_{z}=0)
где (vec{a}=(a_{x};a_{y}))
(vec{b}=(b_{x};b_{y}))
(vec{z}=(z_{x};z_{y}))
являются направляющими векторами прямых а и b.
Теорема 2
Теорема 2
Линии а и b на плоскости будут перпендикулярны, если нормальный вектор прямой а и вектор прямой b взаимно перпендикулярны. Данное условие считается необходимым и достаточным.
Доказательство этой теоремы заключается в применении рассматриваемого условия в том случае, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. Таким образом, имея общее уравнение прямой вида:(
A_{x}+B_{y}+C=0)
а также уравнение прямой в отрезках вида:
(frac{x}{a}+frac{y}{b}=1)
и уравнение прямой с угловым коэффициентом вида y = kx + b, координаты векторов можно определить.
В том случае, когда линия а на плоскости определена с помощью уравнения с угловым коэффициентом:
(y=k_{1}x+b_{1})
и прямая b имеет вид:
(y=k_{2}x+b_{2})
тогда координаты нормальных векторов будут следующие:
((k_{1};-1)) и ((k_{2};-1))
Условие перпендикулярности соответствует выражению:
(k_{1}*k_{2}+(-1)*(-1)=0Leftrightarrow k_{1}*k_{2}=-1)
Теорема 3
Теорема 3
Прямые а и b перпендикулярны на плоскости при необходимом и достаточном условии, при котором один из направляющих векторов этих линий будет коллинеарным нормальному вектору второй прямой.
Данное условие действует при наличии возможности определения направляющего вектора одной прямой и координат нормального вектора другой. Одна прямая должна быть задана каноническим или параметрическим уравнением, а другая представлена в виде общего уравнения прямой, уравнением в отрезках или уравнением с угловым коэффициентом.
Источник
[{Large{text{Скрещивающиеся прямые}}}]
Заметим, что если две прямые лежат в одной плоскости, то, как и в планиметрии, они могут либо пересекаться, либо быть параллельны, либо совпадать. Значит, и угол между такими прямыми ищется так же, как и в планиметрии (напомним, что угол между параллельными прямыми считается равным (0^circ)). А если через две прямые нельзя провести одну плоскость?
Поэтому к трем видам взаимного расположения прямых в плоскости (пересекаются, параллелельны или совпадают) в пространстве добавляется еще один вид: скрещивающиеся прямые.
Определение
Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Угол (alpha) между прямыми — это угол (0^circleqslant
alphaleqslant
90^circ).
Теорема 1: признак скрещивающихся прямых
Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются (рис. 1).
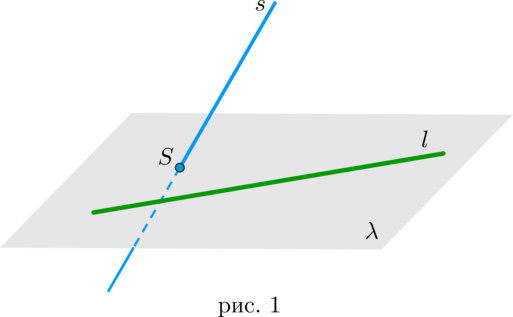
Доказательство
Необходимо доказать, что через прямые (l) и (s) нельзя провести плоскость. Предположим, что это не так, то есть проведем через эти прямые плоскость (pi). Т.к. плоскость (pi) содержит прямую (l) и точку (S), то она совпадает с плоскостью (lambda) по следствию 1 из аксиом. Значит, т.к. прямая (s) лежит в плоскости (pi), то она лежит и в плоскости (lambda), что противоречит условию. Чтд.
Теорема 2
Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой (рис. 2).
Доказательство
Пусть прямые (a) и (b) скрещиваются. Проведем плоскость (beta) через прямую (b) так, чтобы она пересекала прямую (a) в точке (P) (как в предыдущей теореме). Через точку (P) проведем прямую (pparallel b). Т.к. прямые (a) и (p) пересекаются (в точке (P)), то через них проходит единственная плоскость (назовем ее (pi)). Прямая (b) параллельна плоскости (pi) по признаку параллельности прямой и плоскости.
Построенная таким образом плоскость (pi) единственна. Любая другая плоскость, проходящая через прямую (a), будет уже пересекать прямую (p), а следовательно, будет пересекать прямую (b). Чтд.
[{Large{text{Угол между скрещивающимися прямыми}}}]
Определение
Угол между скрещивающимися прямыми – это угол между пересекающимися прямыми, соответственно параллельными двум скрещивающимся прямым.
Таким образом, можно определить следующий алгоритм нахождения угла между скрещивающимися прямыми (рис. 2):
Шаг 1. Через одну из двух скрещивающихся прямых (a) провести плоскость (pi) параллельно другой прямой (b) (по алгоритму, приведенному в теореме 2);
Шаг 2. В этой плоскости найти угол между прямыми (a) и (p) ((pparallel b)). Угол между ними будет равен углу между скрещивающимися прямыми (a) и (b).
[{Large{text{Перпендикулярность прямой и плоскости в пространстве}}}]
Определение
Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
Таким образом, перпендикулярными могут быть как и пересекающиеся прямые (лежащие в одной плоскости), так и скрещивающиеся прямые (не лежащие в одной плоскости).
Утверждение 1
Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая перпендикулярна этой прямой:
[aparallel b, aperp c Longrightarrow bperp c]
Утверждение 2
Две прямые, перпендикулярные третьей прямой, не пересекаются (то есть либо параллельны, либо скрещиваются):
[aperp c, bperp c Longrightarrow acap b=varnothing]
Определение
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Следствие 1
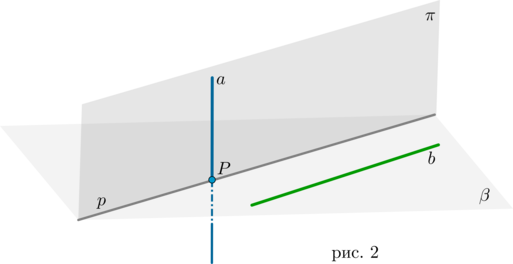
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 3).
(Данное утверждение напрямую следует из утверждения 1.)
Верно и обратное утверждение:
Следствие 2
Если две прямые перпендикулярны плоскости, то они параллельны (рис. 3).
Теорема 3: признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
Доказательство
Пусть прямая (aperp x,aperp y), причем прямые (x, yin pi).
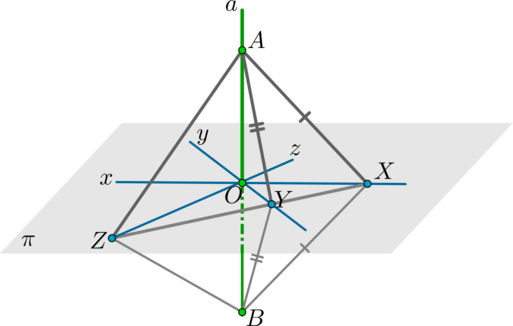
Предположим, что прямая (a) уже проходит через точку (O) пересечения прямых (x) и (y) (если это не так, то проведем через точку (A) прямую (a’), параллельную (a); если (a’) будет перпендикулярна плоскости, то и (a) будет ей перпендикулярна по следствию 1).
Проведем через точку (O) в плоскости (pi) некоторую прямую (z). Проведем также прямую, пересекающую прямые (x, y, z) в точках (X, Y,
Z) соответственно. На прямой (a) по разные стороны от плоскости (pi) отметим точки (A, B) так, чтобы (AO=OB).
Рассмотрим (triangle AXB). Т.к. (XO) – высота (по условию) и медиана (по построению), то (AX=XB). Аналогично для (triangle AYB): (AY=YB). Таким образом, (triangle AXY=triangle BXY) по трем сторонам. Отсюда (angle AXY=angle BXY).
Значит, по двум сторонам и углу между ними (triangle AXZ=triangle
BXZ). Значит, (AZ=BZ). Теперь (triangle AZB) – равнобедренный, причем (ZO) – медиана (по построению). Значит, (ZO) – высота, то есть прямая (a) перпендикулярна прямой (z).
Т.к. прямую (z) мы выбрали произвольно, то это значит, что прямая (a) перпендикулярна любой прямой из плоскости (pi), проходящей через точку (O). Но это значит, что прямая (a) перпендикулярна вообще любой прямой из плоскости, т.к. для любой прямой (z’), не проходящей через точку (O), существует параллельная ей прямая (z), проходящая через точку (O). А раз (aperp z, zparallel z’
Rightarrow aperp z’) (по утверждению 1).
Следствие 3
Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой, и притом только одну.
Следствие 4
Через любую точку пространства проходит прямая, перпендикулярная данной плоскости, и притом только одна.
[{Large{text{Расстояния}}}]
Определение
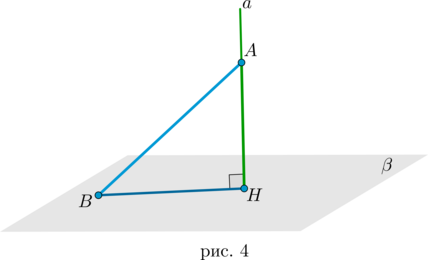
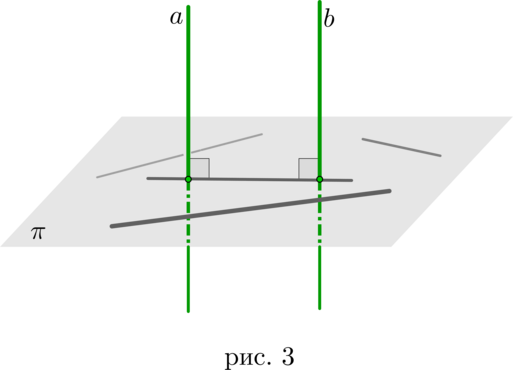
Пусть (aperp beta), причем (acap beta=H). Пусть (Ain a, Bin
beta):

Отрезок (AH) называется перпендикуляром к плоскости (beta).
Отрезок (AB) называется наклонной к плоскости (beta).
Отрезок (BH) называется проекцией наклонной (AB) на плоскость (beta).
Расстояние от точки до плоскости
Длина перпендикуляра (AH) к плоскости (beta) равна расстоянию от точки (A) до плоскости (beta) (рис. 4).
Расстояние между параллельными плоскостями
Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.
Заметим, что расстояние между пересекающимися плоскостями равно нулю.
Расстояние между скрещивающимися прямыми
Длина общего перпендикуляра (h) к обеим скрещивающимся прямым (a) и (b) и есть расстояние между этими скрещивающимися прямыми.
То есть (hperp a, hperp b).
Для того, чтобы найти расстояние между скрещивающимися прямыми, удобно найти расстояние между одной из них и плоскостью, проходящей через вторую прямую параллельно первой.
[{Large{text{Теорема о трех перпендикулярах (ТТП)}}}]
ТТП
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
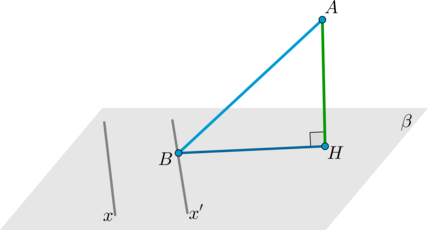
Доказательство
1. Докажем, что из (xperp AB) следует, что (xperp BH).
Заметим, что т.к. (AHperp beta), то (AH) перпендикулярна любой прямой из плоскости (beta).
Проведем прямую (x’parallel x) через точку (B). Рассмотрим плоскость ((AHB)). Прямая (x’) перпендикулярна этой плоскости, т.к. перпендикулярна двум пересекающимся прямым (AB) и (AH) из этой плоскости. Но т.к. (xparallel x’), то и (xperp(AHB) Rightarrow
xperp BH).
2. Случай, когда из перпендикулярности проекции следует перпендикулярность наклонной, доказывается аналогично.
Замечание
Данная теорема является очень важным и незаменимым инструментов во многих задачах стереометрии.
[{Large{text{Угол между прямой и плоскостью. Угол между плоскостями}}}]
Определение
Угол между наклонной прямой и плоскостью — это угол между этой прямой и ее проекцией на данную плоскость. Таким образом, данный угол принимает значения из промежутка ((0^circ;90^circ)).
Если прямая лежит в плоскости, то угол между ними считается равным (0^circ). Если прямая перпендикулярна плоскости, то, исходя из определения, угол между ними равен (90^circ).
Замечание
Таким образом, чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку (A) на этой прямой и провести перпендикуляр (AH) к плоскости. Если (B) – точка пересечения прямой с плоскостью, то (angle ABH) и есть искомый угол (рис. 4).
Определение
Двугранный угол – это геометрическая фигура, образованная прямой (a) (называемой ребром) и двумя полуплоскостями (называемыми гранями), общей границей которых является прямая (a).
Будем считать, что данные полуплоскости не принадлежат одной плоскости (т.к. в этом случае двугранный угол представляет собой просто плоскость с прямой из этой плоскости).
Если отметить по одной точке на каждой полуплоскости, а также две точки на прямой (a) (как показано на рисунке), то двугранный угол можно обозначить как (ABCD).
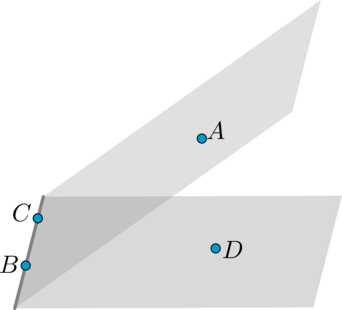
Замечание
Прямая (a) в данном случае является аналогом вершины плоского угла, а полуплоскости – аналогом сторон плоского угла.
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла.
Определение
Если к ребру (a) двугранного угла провести перпендикулярную плоскость (через любую точку), то она пересечет грани двугранного угла по лучам. Угол, образованный данными лучами, называется линейным углом данного двугранного угла.
Замечание
Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла, которым соответствуют четыре линейных угла.
Градусная мера угла между данными плоскостями — это градусная мера меньшего из четырех линейных углов. Таким образом, данный угол принимает значения из промежутка ([0^circ;90^circ]).
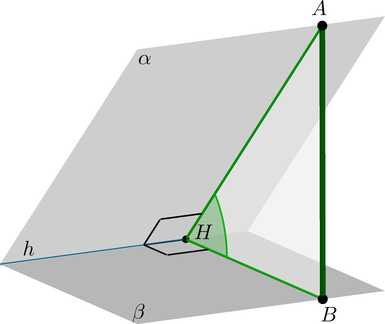
Для того, чтобы найти угол между плоскостями (alpha) и (beta), можно действовать по следующему алгоритму:
Отметить произвольную точку (A) в плоскости (alpha).
Провести (AHperp h), где (h) — линия пересечения плоскостей.
Провести (AB) перпендикулярно плоскости (beta).
Тогда (AB) – перпендикуляр к плоскости (beta), (AH) – наклонная, следовательно, (HB) – проекция. Тогда по ТТП (HBperp h).
Следовательно, плоскость, проходящая через прямые (AH) и (BH), и есть плоскость, перпендикулярная ребру (h) двугранного угла. Значит, (angle AHB) — линейный угол двугранного угла между плоскостями. Градусная мера этого угла равна градусной мере угла между плоскостями.
Заметим, что мы получили прямоугольный треугольник (triangle AHB). Как правило, находить (angle AHB) удобно из него.
[{Large{text{Перпендикулярность плоскостей}}}]
Определение
Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Теорема 4: признак перпендикулярности плоскостей
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Доказательство
Пусть прямая (a) лежит в плоскости (alpha) и перпендикулярна плоскости (beta). Докажем, что тогда плоскости (alphaperp beta).
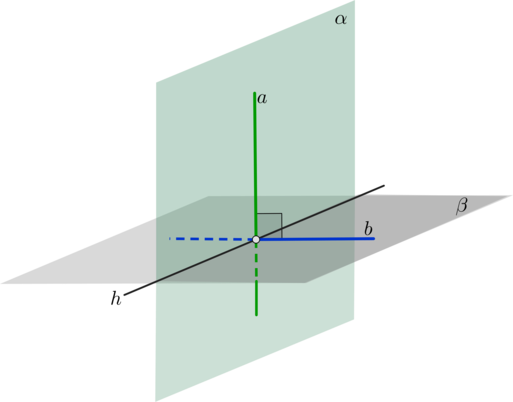
Пусть плоскости пересекаются по прямой (h). Тогда (aperp h) (т.к. (a) перпендикулярна любой прямой из плоскости (beta), а (h), очевидно, лежит в (beta)). Проведем через точку пересечения прямых (a) и (h) прямую (b) в плоскости (beta). Углы, образованные при пересечении прямых (a) и (b) – линейные углы двугранных углов, образованных плоскостями (alpha) и (beta). Но (aperp b), значит, углы, образованные ими, равны (90^circ). Чтд.
Источник
В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Перпендикулярные прямые – основные сведения
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.
То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.
Определение 1
Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.
Перпендикулярность обозначается «⊥», а запись принимает вид a⊥b, что значит, прямая a перпендикулярна прямой b.
Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые Ox, Oz, Oy перпендикулярны попарно: Ox и Oz, Ox и Oy, Oy и Oz.
Перпендикулярность прямых – условия перпендикулярности
Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.
Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.
Теорема 1
Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.
Доказательство 1
Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим a→ и b→. Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a→ и b→. Это возможно только при скалярном произведении векторов a→=(ax, ay) и b→=(bx, by) равном нулю, а запись имеет вид a→, b→=ax·bx+ay·by=0. Получим, что необходимым и достаточным условием перпендикулярности прямых a и b, находящихся в прямоугольной системе координат Оху на плоскости, является a→, b→=ax·bx+ay·by=0, где a→=(ax, ay) и b→=bx, by – это направляющие векторы прямых a и b.
Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b.
Пример 1
Заданы три точки A (8, 6), B(6, 3), C(2, 10) в прямоугольной системе координат Оху. Определить, прямые АВ и АС перпендикулярны или нет.
Решение
Прямые АВ и АС имеют направляющие векторы AB→ и AC→ соответственно. Для начала вычислим AB→=(-2, -3), AC→=(-6, 4). Получим, что векторы AB→ и AC→ перпендикулярны из свойства о скалярном произведении векторов, равном нулю.
AB→, AC→=(-2)·(-6)+(-3)·4=0
Очевидно, что необходимое и достаточное условие выполнимо, значит, АВ и АС перпендикулярны.
Ответ: прямые перпендикулярны.
Пример 2
Определить, заданные прямые x-12=y-73 и x=1+λy=2-2·λ перпендикулярны или нет.
Решение
a→=(2, 3) является направляющим вектором заданной прямой x-12=y-73,
b→=(1, -2) является направляющим вектором прямой x=1+λy=2-2·λ.
Перейдем к вычислению скалярного произведения векторов a→ и b→. Выражение будет записано:
a→,b→=2·1+3·-2=2-6≠0
Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.
Ответ: прямые не перпендикулярны.
Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a→, b→=ax·bx+ay·by+az·bz=0, где a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Пример 3
Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x2=y-1=z+10 и x=λy=1+2·λz=4·λ
Решение
Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a→=(2, -1, 0) и b→=(1, 2, 4) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.
Выражение примет вид a→,b→=2·1+(-1)·2+0·4=0.
Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.
Ответ: прямые перпендикулярны.
Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.
Теорема 2
Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b, это и есть необходимое и достаточное условие.
Доказательство 2
Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида Ax+By+C=0, уравнения прямой в отрезках вида xa+yb=1, уравнения прямой с угловым коэффициентом вида y=kx+b координаты векторов возможно найти.
Пример 4
Выяснить, перпендикулярны ли прямые 3x-y+2=0 и x32+y12=1.
Решение
Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что nα→=(3, -1) – это нормальный вектор для прямой 3x-y+2=0.
Упростим уравнение x32+y12=1 до вида 23x+2y-1=0. Теперь четко видны координаты нормального вектора, которые запишем в такой форме nb→=23, 2.
Векторы na→=(3, -1) и nb→=23, 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0. Получим na→, nb→=3·23+(-1)·2=0.
Необходимое и достаточное условие было выполнено.
Ответ: прямые перпендикулярны.
Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y=k1x+b1, а прямая b – y=k2x+b2, отсюда следует, что нормальные векторы будут иметь координаты (k1, -1) и (k2, -1). Само условие перпендикулярности сводится к k1·k2+(-1)·(-1)=0⇔k1·k2=-1.
Пример 5
Выяснить, перпендикулярны ли прямые y=-37x и y=73x-12.
Решение
Прямая y=-37x имеет угловой коэффициент, равный -37, а прямая y=73x-12- 73.
Произведение угловых коэффициентов дает значение -1, -37·73=-1, то есть прямые являются перпендикулярными.
Ответ: заданные прямые перпендикулярны.
Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.
Теорема 3
Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.
Доказательство 3
Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.
Пример 6
Определить, являются ли заданные прямые x-y-1=0 и x0=y-42 перпендикулярными.
Решение
Получаем, что нормальный вектор прямой x-y-1=0 имеет координаты na→=(1, -1), а b→=(0, 2) – направляющий вектор прямой x0=y-42.
Отсюда видно, что векторы na→=(1, -1) и b→=(0, 2) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t, чтобы выполнялось равенство na→=t·b→. Отсюда вывод, что прямые не являются перпендикулярными.
Ответ: прямые не перпендикулярны.
Источник
