Каким основным свойством обладает пропорция

Что такое пропорция
Определение пропорции:
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
- a : b = c : d
Или вот так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
15 : 5 = 3
9 : 3 = 3
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
- Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4
- Далее преобразовываем это отношение в дробь: 8/4
- Выполняем деление: 8/4 = 2
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
- Запишем в виде отношения: 4 : 2
- Преобразовываем получившееся отношение в дробь: 4/2
- Выполняем деление: 4/2 = 2
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным????
Чтобы ребенок понимал, как еще использовать математику в обычной жизни, запишите его на бесплатный вводный урок в онлайн-школу Skysmart.
Ученики занимаются в интерактивном формате, помогают героям комиксов справиться с коварными задачками, отслеживают прогресс в личном кабинете и не боятся школьных контрольных.
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
- Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
- Далее перемножаем средние члены пропорции: 2 * 12 = 24
- Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
- 6 * 4 = 2 * 12
24 = 24
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
- Перемножаем крайние члены пропорции: 10 * 4 = 40.
- Перемножаем средние члены: 16 * 2 = 32.
- Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
- 10 * 4 ≠ 16 * 2
40 ≠ 32
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Найдите x.
Как решаем:
- По основному свойству пропорции перемножаем множители:
15 * 4 = 3x - Получаем уравнение: 60 = 3x
- 60/3 = x
x = 20.
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Как решаем:
- Записываем чиcла в виде дробей: 18/9 = 24/x
Где x — четвертый член пропорции. - По основному свойству пропорции, перемножаем средние члены: 9 * 24 = 216
- Выводим уравнение 18x = 216
- Находим x:
x = 216 : 18
x = 12 - Проверяем: 9 * 24 = 216, 18 * 12 = 216.
Пропорция составлена верно.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Как решаем:
- Записываем числа в виде дроби: 18/9 = x/8
- Перемножаем множители по основному свойству пропорции: 18 * 8 = 9x
- Находим х:
144 = 9x
144 : 9 = 16
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Найдите y.
Как решаем:
- По основному свойству пропорции перемножаем множители:
20 * 4 = 2y - Получаем уравнение: 80 = 2y
- Находим у:
80/2 = y
x = 40. - Проверяем пропорцию: 20 * 4 = 80, 40 * 2 = 80.
Ответ: в пропорции 20/2 = y/4, y = 40
Есть одна проверенная пропорция, которая выглядит вот так: математика так относится к ученику, как ученик относится к математике — полное равенство отношений.
Чтобы ваш ребенок выстроил добрые пропорциональные отношения с математикой, записывайтесь на бесплатный вводный урок в онлайн-школу Skysmart. Наши преподаватели объяснят самые сложные темы и научат ребенка получать настоящее удовольствие от решения задачек.
Источник
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение равно отношению
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение не пропорционально отношению .
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
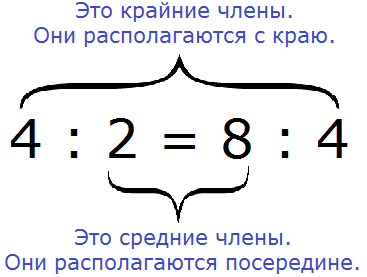
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
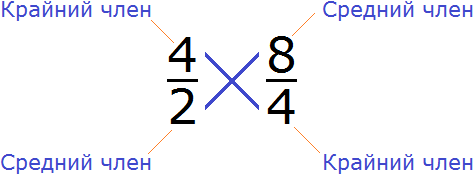
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
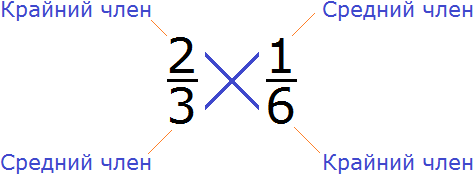
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Источник
Чтобы узнать название темы урока, обратите внимание на картинку.
Попробуйте отгадать ребус.

На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.
Слово «пропорция» (proportio) в переводе с латинского – соразмерность, отношение частей (соотношение).
В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.
Пропорции применяли с древности при решении различных задач.
Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.
Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.
В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.
В швейных технологиях – для изменения размеров выкройки изделия до нужного размера.
В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.
В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.
В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.

Разберем, что же такое пропорция в математическом понимании.
Возьмем два отношения: (mathbf{frac{36}{9}}) и (mathbf{frac{12}{3}}) и эти отношения равны, так как (mathbf{36div9=4}) и (mathbf{12div3=4}), значит (mathbf{frac{36}{9}= frac{12}{3}})
Равенство двух отношений называют пропорцией.

С помощью букв запишем пропорцию из двух отношений так: (mathbf{adiv b= cdiv d }) или (mathbf{frac{a}{b}= frac{c}{d}}).
Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».
Все члены пропорции не равны нулю: (mathbf{aneq 0, bneq 0, cneq 0, dneq 0}).
Если внимательно посмотреть на пропорцию (mathbf{{a}div{b}= {c}div{d}}), то можно заметить будто величины a и d стоят по краям равенства, а величины b и c в середине пропорции, в связи с этим легко запомнить, что:
Числа a и d называют крайними членами пропорции.
Числа b и c называют средними членами пропорции.

У меня есть дополнительная информация к этой части урока!
Закрыть
В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.
Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.
В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.
Обозначают число «золотого сечения» математической буквой (mathbf{varphi}) (фи).
Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».
Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».
Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».
Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».
Спиралевидная форма ракушек тоже описывается числом (mathbf{varphi}) (фи).


«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека
Теория отношений и пропорции изложена в «Началах» древнегреческого математика Эвклида (3 век до н.э.), в этом же труде было подробно описано и доказано основное свойство пропорции.
Давайте рассмотрим, какими же свойствами обладает пропорция и каким правилам подчиняется.
Пропорция, в которой произведение крайних членов равно произведению средних членов, является верной пропорцией.
Обратное утверждение так же является истинным.
Если произведение крайних членов равно произведению средних членов, то пропорция верна.
Данное свойство пропорции – это основное свойство пропорции.
Найдем произведение крайних членов пропорции (mathbf{adiv b= cdiv d }) и произведение средних членов этой пропорции, получим: (mathbf{acdot d= ccdot b }).
Пример
Дана пропорция (mathbf{frac{3}{5}= frac{6}{10}}), где числа 3, 10 – это крайние члены этой пропорции, 5, 6 – это средние члены пропорции.
По основному свойству пропорции
(mathbf{3cdot 10= 5cdot 6 = 30 }), значит пропорция (mathbf{frac{3}{5}= frac{6}{10}}) верная.
Если в верной пропорции поменять местами средние члены или крайние члены, то получатся новые верные пропорции.
Дополнительный материал
Пропорция обладает рядом других интересных свойств.
Так как члены пропорции отличны от нуля, то справедливо следующее: если в пропорции перевернуть отношения, то в результате получится тоже верная пропорция.
(mathbf{frac{a}{b}= frac{c}{d}})перевернем отношения и получим (mathbf{frac{b}{a}= frac{d}{c}})
Пример
(mathbf{frac{12}{2}= frac{6}{1}}) перевернем отношения и получим (mathbf{frac{2}{12}= frac{1}{6}}) , проверим полученное равенство.
По основному свойству пропорции (mathbf{2cdot 6= 12cdot 1 = 12 })
Новая пропорция (mathbf{frac{2}{12}= frac{1}{6}}) является верной.
При решении задач иногда используют правило увеличения и уменьшения пропорции.
Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то равенство сохранится в следующих случаях:
Увеличение пропорции: (mathbf{frac{a + b}{b}= frac{c + d}{d}}),
Уменьшение пропорции: (mathbf{frac{a – b}{b}= frac{c – d}{d}}).
Пропорция обладает еще одним свойством: нахождение пропорции сложением или вычитанием членов пропорции.
Если есть пропорция (mathbf{frac{a}{b}= frac{c}{d}}), то справедливо
составление пропорции сложением (mathbf{frac{a + c}{b + d}= frac{a}{b} = frac{c}{d}})
составление пропорции вычитанием (mathbf{frac{a – c}{b – d}= frac{a}{b} = frac{c}{d}})
Применяя основное свойство пропорции, можно найти неизвестный член этой пропорции.
Решить пропорцию – это значит найти средний или крайний член пропорции.
Для решения пропорции с неизвестным крайним членом, при условии, что все остальные члены пропорции определены, необходимо умножить средние члены пропорции и полученный результат разделить на известный крайний член пропорции.
Пример 1
(mathbf{frac{a}{2}= frac{6}{1}})
решите пропорцию, найдя значение крайнего члена пропорции (a).
(mathbf{a = frac{2 cdot 6}{1}= 12})
Подставьте значение крайнего члена (а) в пропорцию
(mathbf{frac{12}{2} = frac{6}{1}= 6}) получили верную пропорцию.
Для решения пропорции с неизвестным средним членом, при условии, что все остальные члены пропорции определены, необходимо умножить крайние члены пропорции и полученный результат разделить на известный средний член пропорции.
Пример 2
(mathbf{frac{12}{b}= frac{6}{1}}) решим пропорцию, найдем значение среднего члена пропорции (b)
(mathbf{b = frac{12 cdot 1}{6}= 2})
Подставим значение среднего члена (b) в пропорцию
(mathbf{frac{12}{2} = frac{6}{1}= 6}) получили верную пропорцию.
Часто для решения пропорции используют способ «крест-накрест».
Чтобы вычислить неизвестный член пропорции, нужно перемножить известные члены пропорции, находящиеся на диагональной линии, а затем разделить результат на оставшееся известное число, находящееся на диагональной линии с неизвестным членом пропорции.

Пример 3
(mathbf{frac{8}{2}= frac{x}{8}}) , где x– неизвестный член пропорции,
(mathbf{8 cdot 8 = 64}) перемножили известные значения членов пропорции, находящиеся по диагонали в этой пропорции.
Полученный результат делим на известный член, находящийся по диагонали с неизвестным.
(mathbf{x = 64 div 2 = 32})
Получили пропорцию (mathbf{frac{8}{2} = frac{32}{8}= 4}), пропорция верна
К решению пропорции сводятся многие математические задачи и уравнения.
Рассмотрим некоторые из них.
Задача 1
Решите уравнение (mathbf{frac{y}{1,5}= frac{4}{3}})
Решение:
Найдем неизвестный член пропорции y, применив основное свойство пропорции.
Составим уравнение и решим его
(mathbf{3 cdot y = 1,5 cdot 4})
(mathbf{y = frac{1,5 cdot 4}{3}})
(mathbf{y = frac{6}{3}})
(mathbf{y = 2})
Ответ: (mathbf{y = 2})
Задача 2
На товар была сделана скидка 150 рублей, что составляет 15% от первоначальной цены товара.
Чему равна первоначальная цена товара?
Решение:
В задачах на проценты целое принимают за 100% или 1.
Неизвестную величину обозначают буквой (чаще всего x или y).
Величины в задаче должны быть приведены в одинаковые единицы измерения.
Модель решения задач с процентами при помощи пропорции можно представить в виде таблицы:

Или с помощью логической схемы

В результате пропорция получается такого вида:

Исходя из вышеизложенного, решение задачи будет выглядеть так:
Пусть x (рублей) – первоначальная цена товара, она составляет 100%.
Часть от целого (первоначальной цены) = 15%
Составим условную запись задачи:
x (руб.) – 100%
150 (руб.) – 15%
Составим пропорцию:(mathbf{frac{x}{150}= frac{100}{15}})
По основному свойству пропорции решим уравнение.
(mathbf{x = frac{150 cdot 100}{15}})
(mathbf{x = 1000 (руб.)}) первоначальная цена товара.
Ответ: (mathbf{x = 1000 (руб.)})
Задача 3
За 5 кг Муки заплатили 195 рублей. Какова стоимость 3 кг этой муки?
Решение:
Пусть x (рублей)- стоимость 3 кг муки.
Составим условную запись задачи.
5 (кг)- 195 (руб)
3 (кг)- x (руб)
Составим пропорцию: (mathbf{frac{5}{3}= frac{195}{x}})
По основному свойству пропорции решим уравнение:
(mathbf{x = frac{3 cdot 195}{5}})
(mathbf{x = 117 (руб.)}) стоят 3 кг муки.
Ответ: (mathbf{x = 117 (руб)})
Пройти тест
Источник
