Каким свойством обладает центр качания

Рассмотрим так называемый
математический маятник – материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.
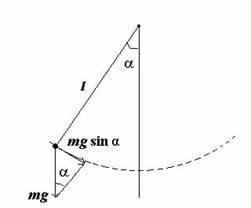
| Второй закон | для такого маятника запишется так: |
,
или
Сравнивая
его с дифференциальным уравнением гармонических
колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на
a,
что можно сделать при малых a. Следовательно, колебания математического маятника
можно считать гармоническими только при малых углах отклонения от положения
равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси
O (оси качания), не проходящей через центр инерции тела C.
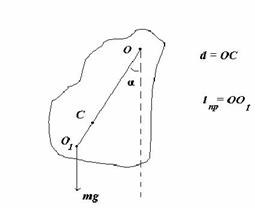
На рисунке обозначено:
ось качания маятника – неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О – пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр – длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника – О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
где J – момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда
sin
a
@
a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
Из определения приведенной длины физического маятника найдем, что:
Здесь Jc – момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через
О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке
О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки
О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый
линейный гармонический осциллятор), то есть материальную точку массой
m, совершающую линейные гармонические колебания под действием упругой силы
F:
F = – k x (для пружины это – закон Гука).
Второй закон Ньютона для такого маятника запишется так:
,
или
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
Источник
Колебания — это процессы, которые имеют какую либо степень повторяемости во времени.
Свободные (собственные) колебания — это колебания, которые предоставляют сами себе системы, вызванные первоначальным кратковременным внешним возбуждением.
Колебательная система — это такая система, которая способная производить свободные колебания.
Колебательная система соответствует следующим условиям:
- необходимо положение устойчивого равновесия;
- необходим фактор, не позволяющий системе остановиться в положении равновесия в процессе колебаний;
- трение в системе должно быть небольшим, а собственная частота колебательной системы обусловливается только параметрами системы.
Амплитуда колебаний — это максимальное значение величины (для механических колебаний это смещение), которая совершает колебания.
Период колебаний — это самый маленький отрезок времени, через который система совершает колебания, снова возвращается в исходное состояние, т. е. в начальный момент.
Частота колебаний — это физическая величина, равная числу колебаний, которые совершаются в единицу времени.
Циклическая частота — это характеристика гармонических колебаний, совершаемых за
Фаза колебаний — это аргумент функции, который периодически изменяется.
Затухающие колебания — это собственные колебания, у которых амплитуда уменьшается со временем, что обусловлено потерями энергии колебательной системой.
Коэффициент затухания и логарифмический декремент затухания — это характеристика быстроты уменьшения амплитуды в случае механических колебаний, где энергия убывает за счет действия сил трения и других сил сопротивления.
Декремент затухания — это количественная характеристика быстроты затухания колебаний, которая определяется натуральным логарифмом отношения двух последовательных максимальных отклонений , колеблющейся величины в одну сторону:
Декремент затухания — величина, обратная числу колебаний, по истечении которых амплитуда убывает в: е раз е = 2,71828). Промежуток времени, необходимый для этого, называется временем релаксации.
Дифференциальное уравнение малых затухающих колебаний системы:
Вынужденные колебания — это колебания, которые возникают под действием внешней периодической силы.
Дифференциальное уравнение вынужденных колебаний:
Резонанс — это процесс резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты , вынуждающей силы к собственной циклической частоте колебательной системы.
Автоколебания — это незатухающие колебания физической системы, которые способны существовать без воздействия на нее внешних сил.
Автоколебательная система — это физическая система, где имеет место существовать автоколебания.
Автоколебательная система состоит из следующих частей:
- колебательная система, в которой параметры определяют частоту автоколебаний;
- источник энергии, который способствует поддержанию колебаний;
- клапан, который регулирует поступление энергии в колебательную систему;
- положительная обратная связь, которая способна управлять клапаном в колебательной системе.
Обратная связь — это воздействие результатом какого-либо процесса на его протекание.
Обратная связь бывает:
- положительная — это связь, которая приводит к увеличению отклонения;
- отрицательная — это связь, которая приводит к уменьшению отклонения.
Периодические колебания — это колебания, которые имеют изменяющиеся значения физических величин, но которые повторяются через равные отрезки времени.
Смещение — это физическая величина, которая является характеристикой колебаний, равная отклонению тела от положения равновесия в данный момент времени.
Математический, физический, пружинный маятники.
Математический маятник — это тело малых размеров, подвешенное на тонкой нерастяжимой нити, масса которой ничтожно мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити .
Составляющая силы тяжести при отклонении маятника из положения равновесия на некоторый угол ф , где знак «минус» означает, что касательная составляющая на- правлена в сторону, противоположную отклонению маятника. Второй закон Ньютона для математического маятника запишется: , где x — линейное смещение маятника от положения равно- весия по дуге окружности, l — радиус.
Угловое смещение будет равно
Для малых колебаний математического маятника второй закон Ньютона записывается в виде:
Если математический маятник совершает малые колебания, то он является гармоническим осциллятором. Собственная частота малых колебаний математического маятника:
Период малых колебаний математического маятника определяется:
Физический маятник — это тело, которое является твердым, производящее колебания в поле каких-либо сил относительно точки, которая не является центром масс этого тела, или горизонтальной оси.
Второй закон Ньютона для физического маятника принимает вид:
Собственная частота малых колебаний физического маятника:
Период малых колебаний физического маятника определяется:
Круговая частота свободных колебаний физического маятника определяется выражением:
Центр качания физического маятника — это точка, где необходимо сосредоточить всю массу физического маятника, чтобы его период колебаний оставался постоянным.
Физический маятник обладает следующим замечательным свойством: если физический маятник подвесить за центр качания, то его период колебаний будет постоянным, а прежняя точка подвеса станет новым центром качания.
Пружинный маятник — это колебательная система, которая состоит из груза, подвешенного к абсолютно упругой пружине.
Пружинный маятник совершает гармонические колебания с циклической частотой:
, где k — коэффициент жесткости.
Период пружинного маятника определяется:
Уравнение движения пружинного маятника при этом имеет вид:
Источник
- Главная
- Вопросы & Ответы
- Вопрос 14090850
Пармезан Черница
более месяца назад
Просмотров : 2
Ответов : 1
Лучший ответ:
Мари Умняшка
это качалка треножорный зал
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Главный Попко
Решите уравнение PLEASE!!! x-119/x 7=-5
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Онтонио Веселко
Помогите сделать задание N6
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Картинок: 1
Таня Масян
сочинить сочинение про стих Бородино
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов : 1
Мари Умняшка
Как по английски будет “выглядит как”? Например: выглядит как гном, выглядит как мальчик и т. д.
более месяца назад
Смотреть ответ
Просмотров : 1
Ответов : 1
Суррикат Мими
Повысить частоту мутаций в популяции можно Выберите один ответ: a. скрещиванием чистых линий b. межвидовыми скрещиваниями c. действием рентгеновских лучей на особей d. скрещиванием гетерозиготных организмов
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов :
Источник
Оборотный маятник используется для точного определения ускорения свободного падения. В основе этого метода определения ускорения свободного падения лежит теорема Гюйгенса: если физический маятник подвесить за центр качания О1, то его период не изменится, а прежняя точка подвеса О сделается новым центром качания[2, с.211] (рис.1).Оборотный маятник позволяет с точностью до 0,5% определить положение точки подвеса и центра качания. Расстояние между этими точками называется приведенной длиной физического маятника (оборотный маятник это частный случая физического маятника). Так как период колебаний физического маятника равен периоду колебаний математического маятника, если его приведенная длина равна длине математического маятника, то для определения ускорения свободного падения можно воспользоваться формулой математического маятника:
, (1)
здесь Т – период колебаний физического маятника, l0 – его приведенная длина, g – ускорение свободного падения. Таким образом, определение ускорения свободного падения сводится к определению периода колебаний физического маятника и его приведенной длины.
Получим выражение (1), зная основной закон динамики вращения твердого тела относительно неподвижной оси вращения О:
I0 ε0=M0, (2)
здесь I0 – момент инерции твердого тела относительно данной оси О, ε0 – угловое ускорение относительно той же оси вращения, M0 – результирующий момент внешних сил относительно осиО. Все кинематические и динамические характеристики вращения твердого тела относительно неподвижной оси выбираются с надлежащим знаком [2, c.173]. Условимся величины, определяющие повороты по часовой стрелке выбирать со знаком «-»,против часовой стрелки со знаком «+».
Физическим маятником называют любое твёрдое тело, имеющее неподвижную ось вращения О, не совпадающую с центром масс тела (рис. 1). При отклонении маятника от положения равновесия на угол φ возникает возвращающий момент силы тяжести относительно этой оси
, (3)
где m — масса тела, l — расстояние между осью вращения О и центром масс С («-» свидетельствует о том, что φ и N имеют противоположные знаки). В этом случае уравнение динамики вращательного движения твёрдого тела относительно оси запишется в виде:
, (4)
где I — момент инерции тела относительно оси вращения, — угловое ускорение. При малых углах отклонения , тогда
. (5)
Сравнивая полученное уравнение с известным общим уравнением гармонических колебаний
, (6)
приходим к выводу, что физический маятник совершает свободные гармонические колебания с частотой и периодом соответственно
и . (7)
По теореме Штейнера I = Ic +ml2, (8)
где Ic — момент инерции тела относительно оси, проходящей через цент масс C, l — расстояние между центром масс и действительной осью вращения.
,
Обозначив
, (9) (20)
после подстановки (9) в (7) получаем интересующую нас формулу (1)
(1) (21)
Как уже отмечалось, величина l0 называется приведенной длиной физического маятника. Поскольку (1) совпадает с периодом свободных колебаний математического маятника длиной l0, то под приведенной длиной физического маятника понимается длина такого математического маятника, период свободных колебаний которого совпадает с периодом свободных колебаний данного физического маятника.
Если отложить от точки подвеса О вдоль прямой ОС отрезок ОО1, длина которого равна приведенной длине физического маятника l0, то точка О1 станет центром качания. Центр качания можно определить как математическую точку, в которой надо сосредоточить всю массу физического маятника, чтобы период его колебаний остался без изменений. Легко доказать (сделайте это самостоятельно), во-первых, что l0> l, т.е. точка подвеса и центр качания лежат по разные стороны от центра масс С, во-вторых, всем точкам подвеса одинаково удаленным от центра масс маятника С соответствует одна и та же приведенная длина, а следовательно один и тот же период колебаний Т. Точка подвеса и центр качания являются взаимными или сопряженными точками в том смысле, что если маятник подвесить за ту или другую точку, то в соответствии с теоремой Гюйгенса периоды колебаний совпадут (докажите это самостоятельно). Точка подвеса и центр качания находятся по разные стороны от центра масс и расположены асимметрично относительного него (доказательство см. в [2, с.213]). Физический маятник, который можно подвешивать за любую из сопряженных точек называется оборотным. Существуют разнообразные конструкции оборотных маятников.
ОПИСАНИЕ УСТАНОВКИ
Оборотный маятник в данной лабораторная установка показана на рис.2. Правый и левый болты с резцами треугольного сечения закрепляются на одинаковой высоте так, чтобы масса маятника распределялась равномерно по обеим точкам приложения нагрузки, и маятник находился в строго вертикальном положении. Для точного измерения ускорения свободного падения стол должен находиться в устойчивом положении.
Опорные втулки (А и В соответственно) прикрепляются по краям цилиндрического стержня.

Рис. 2 Экспериментальная установка «Оборотный маятник»
Период колебаний маятника определяется для малых амплитуд колебаний при помощи светового барьера. Переключатель на световом барьере должен быть установлен в крайнее правое положение .
Идея метода
 Метод основан на определении приведенной длины физического маятника и соответствующих ей периодов колебаний, что позволяет рассчитать ускорение свободного падения по формуле (1).
Метод основан на определении приведенной длины физического маятника и соответствующих ей периодов колебаний, что позволяет рассчитать ускорение свободного падения по формуле (1).
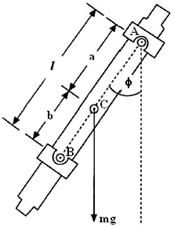
Оборотный маятник (рис.3) состоит из длинного цилиндрического стержня, на котором закрепляются две подвижные опорные втулки А и В. Колебания маятника осуществляются поочередно вокруг осей, проходящих через вырезы этих втулок.
Обозначим расстояние от выреза опорной втулки А до центра масс С через а; расстояние от выреза опорной втулки
В до центра масс С через b; расстояние между осями l.
Рис. 3 Оборотный маятник
Пусть ТА и ТВ – периоды колебаний маятника относительно осей, проходящих соответственно через вырезы опорных втулок А и В. В соответствии с формулой (7) можно записать:
(10)
где IA и IB – моменты инерции маятника относительно осей, проходящих через вырезы опорных втулок.
Возведем каждое из выражений (10) в квадрат, умножим первое на а, второе – на b и вычтем второе уравнение из первого:
(11)
Моменты инерции IA и IB можно определить, воспользовавшись еще одной теоремой Штейнера: «Момент инерции тела относительно произвольной оси равен сумме двух слагаемых: момента инерции относительно параллельной ей оси, проходящей через центр масс IC, и произведения массы тела на квадрат расстояния между центром масс и рассматриваемой произвольной осью».
Таким образом,
(12)
Подставив соотношение (12) в (11), получим:
(13)
Если подобрать положения опорных втулок А и В таким образом, чтобы выполнялось соотношение ТА = ТВ = Т0, то формула (13) значительно упрощается, что позволяет получить рабочую формулу для определения ускорения силы тяжести при помощи оборотного маятника:
или уже знакомая нам формула (1), преобразованная относительно g
(14)
где l = a + b – расстояние между вырезами опорных втулок в случае равенства периодов колебаний относительно каждой из осей (ТА = ТВ = Т0) и есть приведенная длина оборотного маятника. Зная l и Т0 , по формуле (14) можно рассчитать ускорение свободного падения g.
Технические характеристики измерительных приборов установки
Таблица 1
| №п.п. | Название прибора | Пределы измерений | Число делений | Цена деления | Абсолютная погрешность |
| Счетчик колебаний | 0.01с | ||||
| Измерительная рулетка | 1 мм |
Выполнение работы
1. Опорные втулки А и В закрепите симметрично на расстоянии 7—10 см от концов стержня.
2. Установите маятник так, чтобы опорная втулка А служила осью качания. Отклоните маятник от положения равновесия на угол, не превышающий 20. Проведите 5—7 измерений периода колебаний ТА. Найдите среднее значение периода ТА.
3. Переверните маятник так, чтобы опорная втулка В стала осью качания оборотного маятника. При этом, не меняя положения втулки А, опорную втулку В установите на расстоянии l = 60 см от неё. Проведите 2—3 измерений периода колебаний ТВ. Найдите среднее значение периода ТВ. Результат занесите в таблицу 2.
Таблица 2
4. Каждый раз, уменьшая расстояние между втулками на 2 см, проведите измерения ТВ и результаты измерений занесите в таблицу 2. Рекомендуемый диапазон расстояний между опорными втулками l: 60 – 34 см. Постройте график зависимости ТВ(l). Графически определите расстояния l1 и l2, для которых ТВ = ТА (см. пример рис.4).
5. Перемещения опорной втулки В приводят к изменению момента инерции маятника и положения его центра масс. Следовательно, и меняется значение периода колебаний относительно втулки А. Чтобы учесть эти изменения, необходимо провести измерение периодов колебаний ТА и ТВ при одинаковых значениях l. Для этого установите между втулками расстояние l = l1– 3 см (положение втулки А не меняем). Определите поочередно периоды ТА и ТВ на выбранном расстоянии.
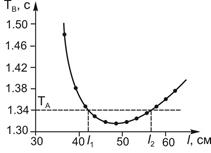
Рис. 4 Пример графика зависимости TВ(l)
6. Повторите п. 5, изменяя расстояние l в интервале от (l1– 3) см до (l1+ 3) см с шагом в 1 см. Результаты занесите в таблицу 3.
Таблица 3
| l, см | l1– 3 см | l1– 2 см | … | l1+ 3 см |
| ТА, с | ||||
| ТВ, с |
7.
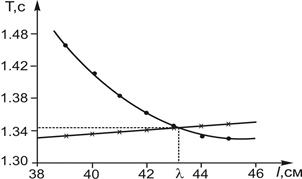 |
Постройте графики зависимостей ТА = f(l) и ТВ = f (l) на одном листе миллиметровой бумаги (рис.5). Приведенная длина маятника соответствует точке пересечения кривых (см. рис.5) l=λ, по этому графику определяют и период Т0, соответствующий этому расстоянию между втулками А и В. Установите опорную втулку В на расстоянии l=λ от втулки А, по-прежнему не меняя положения втулки А. Убедитесь, что период колебаний маятника на каждой опорной втулке соответствует Т0.
Рис. 5 Определение приведенной длины
оборотного маятника графическим способом
8. По формуле (14) рассчитайте ускорение свободного падения. Оцените погрешность, учитывая погрешности измерительных приборов, приведенные в таблице1.
9. Сравните периоды колебаний для физического и математического маятников, если длина математического маятника равна приведенной длине физического .
Источник
