Каким свойством обладает центр качания физического маятника

Рассмотрим так называемый
математический маятник – материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.
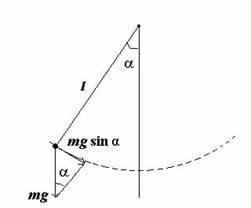
| Второй закон | для такого маятника запишется так: |
,
или
Сравнивая
его с дифференциальным уравнением гармонических
колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на
a,
что можно сделать при малых a. Следовательно, колебания математического маятника
можно считать гармоническими только при малых углах отклонения от положения
равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси
O (оси качания), не проходящей через центр инерции тела C.
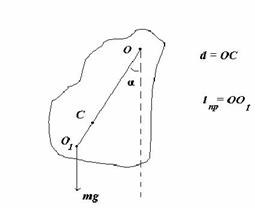
На рисунке обозначено:
ось качания маятника – неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О – пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр – длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника – О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
где J – момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда
sin
a
@
a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
Из определения приведенной длины физического маятника найдем, что:
Здесь Jc – момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через
О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке
О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки
О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый
линейный гармонический осциллятор), то есть материальную точку массой
m, совершающую линейные гармонические колебания под действием упругой силы
F:
F = – k x (для пружины это – закон Гука).
Второй закон Ньютона для такого маятника запишется так:
,
или
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
Источник
Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Дифференциальное уравнение движения физического маятника[править | править код]
Момент инерции относительно оси, проходящей через точку подвеса по теореме Штайнера:
где — момент инерции относительно оси проходящей через центр тяжести;
— эффективный радиус инерции относительно оси, проходящей через центр тяжести.
Динамическое уравнение произвольного вращения твёрдого тела:
где — суммарный момент сил, действующих на тело относительно оси вращения.где — момент сил, вызванный силой тяжести;
— момент сил, вызванный силами трения среды.
Момент вызванный силой тяжести зависит от угла отклонения тела от положения равновесия:
Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:
.
Если разделить обе части уравнения на и положить то уравнение будет:
Такое уравнение аналогично уравнению колебаний математического маятника длиной . Величина называется приведённой длиной физического маятника.
Центр качания физического маятника[править | править код]
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника.
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . При этом уравнение движения не изменится.
Теорема Гюйгенса[править | править код]
Формулировка[править | править код]
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Доказательство[править | править код]
Вычислим приведенную длину для нового маятника:
.
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период колебаний физического маятника[править | править код]
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую и правую часть этого уравнения на . Тогда:
.
Интегрируя это уравнение, получаем:
,где — произвольная постоянная.
Её можно найти из граничного условия, что в моменты . Получаем:
Подставляем и преобразовываем получившееся уравнение:
Отделяем переменные и интегрируем это уравнение:
Удобно сделать замену переменной полагая . Тогда искомое уравнение принимает вид:
Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
Здесь — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:
Период малых колебаний физического маятника[править | править код]
Если — случай малых максимальных угловых отклонений от равновесия, то так как разложение сунуса в ряд Маклорена и уравнения движения переходит в уравнение гармонического осциллятора без трения:
Период колебания маятника в этом случае:
В иной формулировке: если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):
См. также[править | править код]
- Математический маятник
Ссылки[править | править код]
- маятник — статья из Большой советской энциклопедии.
Источник
Колебания — это процессы, которые имеют какую либо степень повторяемости во времени.
Свободные (собственные) колебания — это колебания, которые предоставляют сами себе системы, вызванные первоначальным кратковременным внешним возбуждением.
Колебательная система — это такая система, которая способная производить свободные колебания.
Колебательная система соответствует следующим условиям:
- необходимо положение устойчивого равновесия;
- необходим фактор, не позволяющий системе остановиться в положении равновесия в процессе колебаний;
- трение в системе должно быть небольшим, а собственная частота колебательной системы обусловливается только параметрами системы.
Амплитуда колебаний — это максимальное значение величины (для механических колебаний это смещение), которая совершает колебания.
Период колебаний — это самый маленький отрезок времени, через который система совершает колебания, снова возвращается в исходное состояние, т. е. в начальный момент.
Частота колебаний — это физическая величина, равная числу колебаний, которые совершаются в единицу времени.
Циклическая частота — это характеристика гармонических колебаний, совершаемых за
Фаза колебаний — это аргумент функции, который периодически изменяется.
Затухающие колебания — это собственные колебания, у которых амплитуда уменьшается со временем, что обусловлено потерями энергии колебательной системой.
Коэффициент затухания и логарифмический декремент затухания — это характеристика быстроты уменьшения амплитуды в случае механических колебаний, где энергия убывает за счет действия сил трения и других сил сопротивления.
Декремент затухания — это количественная характеристика быстроты затухания колебаний, которая определяется натуральным логарифмом отношения двух последовательных максимальных отклонений , колеблющейся величины в одну сторону:
Декремент затухания — величина, обратная числу колебаний, по истечении которых амплитуда убывает в: е раз е = 2,71828). Промежуток времени, необходимый для этого, называется временем релаксации.
Дифференциальное уравнение малых затухающих колебаний системы:
Вынужденные колебания — это колебания, которые возникают под действием внешней периодической силы.
Дифференциальное уравнение вынужденных колебаний:
Резонанс — это процесс резкого возрастания амплитуды вынужденных колебаний при приближении циклической частоты , вынуждающей силы к собственной циклической частоте колебательной системы.
Автоколебания — это незатухающие колебания физической системы, которые способны существовать без воздействия на нее внешних сил.
Автоколебательная система — это физическая система, где имеет место существовать автоколебания.
Автоколебательная система состоит из следующих частей:
- колебательная система, в которой параметры определяют частоту автоколебаний;
- источник энергии, который способствует поддержанию колебаний;
- клапан, который регулирует поступление энергии в колебательную систему;
- положительная обратная связь, которая способна управлять клапаном в колебательной системе.
Обратная связь — это воздействие результатом какого-либо процесса на его протекание.
Обратная связь бывает:
- положительная — это связь, которая приводит к увеличению отклонения;
- отрицательная — это связь, которая приводит к уменьшению отклонения.
Периодические колебания — это колебания, которые имеют изменяющиеся значения физических величин, но которые повторяются через равные отрезки времени.
Смещение — это физическая величина, которая является характеристикой колебаний, равная отклонению тела от положения равновесия в данный момент времени.
Математический, физический, пружинный маятники.
Математический маятник — это тело малых размеров, подвешенное на тонкой нерастяжимой нити, масса которой ничтожно мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити .
Составляющая силы тяжести при отклонении маятника из положения равновесия на некоторый угол ф , где знак «минус» означает, что касательная составляющая на- правлена в сторону, противоположную отклонению маятника. Второй закон Ньютона для математического маятника запишется: , где x — линейное смещение маятника от положения равно- весия по дуге окружности, l — радиус.
Угловое смещение будет равно
Для малых колебаний математического маятника второй закон Ньютона записывается в виде:
Если математический маятник совершает малые колебания, то он является гармоническим осциллятором. Собственная частота малых колебаний математического маятника:
Период малых колебаний математического маятника определяется:
Физический маятник — это тело, которое является твердым, производящее колебания в поле каких-либо сил относительно точки, которая не является центром масс этого тела, или горизонтальной оси.
Второй закон Ньютона для физического маятника принимает вид:
Собственная частота малых колебаний физического маятника:
Период малых колебаний физического маятника определяется:
Круговая частота свободных колебаний физического маятника определяется выражением:
Центр качания физического маятника — это точка, где необходимо сосредоточить всю массу физического маятника, чтобы его период колебаний оставался постоянным.
Физический маятник обладает следующим замечательным свойством: если физический маятник подвесить за центр качания, то его период колебаний будет постоянным, а прежняя точка подвеса станет новым центром качания.
Пружинный маятник — это колебательная система, которая состоит из груза, подвешенного к абсолютно упругой пружине.
Пружинный маятник совершает гармонические колебания с циклической частотой:
, где k — коэффициент жесткости.
Период пружинного маятника определяется:
Уравнение движения пружинного маятника при этом имеет вид:
Источник
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен
М = –mglsinj,
где m –масса маятника, а l–расстояние между точкой подвеса ицентром масс маятника. Знак “–” означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:
b = М / I = – (mgl/ I) sin j,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса. В случае малых колебаний (j≤ 5°) это уравнение переходит в дифференциальное уравнение собственных незатухающих колебаний:
,
решением которого является функция:
j = А cos (w0t + a0),
где через w0 обозначена угловая частота колебаний:
w0 = (mgl/ I)1/2.
Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w0 которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Период колебаний физического маятника определяется выражением:
.
Из сопоставления формул и следует, что математический маятник с длиной lпр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину lпр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка 0′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде
I = I0 + ml2,
где I0 – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.
Подставив I = I0 + ml2 в lпр = (I/ml) , получаем: lпр = (I0/ml) + l , откуда следует, что приведенная длина lпр всегда больше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′.Приведенная длина в этом случае будет равна: lпр‘ = (I0/ml‘) + l‘ , где l‘ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l‘ = lпр – l, имеем:
lпр‘ = I0/m(lпр – l) + lпр – l = lпр + [(I0 + ml2) – mlпрl] /m(lпр – l).
Выражение, стоящее в квадратных скобках, равно нулю, поскольку I0 + ml2 = I – это момент инерции относительно первоначальной оси вращения; этой же величине равно выражение mlпрl.Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр качания 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
На свойстве взаимности основано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы П1 и П2, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно lпр. Измерив период колебаний маятника Т0 и определив lпр, при помощи формулы можно найти ускорение силы тяжести g:
.
Источник
Физическим маятником называется твердое тело, способное совершать
колебания вокруг неподвижной точки, не совпадающей с его центром инерции
Физическим маятником называется твердое тело, способное
совершать колебания вокруг неподвижной точки, не совпадающей с его центром
инерции. В положении равновесия центр инерции маятника С под точкой подвеса
маятника О, на одной с ней вертикали (рис. 170). При отклонении маятника от
положения равновесия на угол возникает вращательный момент,
стремящийся вернуть маятник в положение равновесия. Этот момент равен
(67.1) |
где m— масса
маятника» а l-расстояние между точкой подвеса и центром инерции маятника. Знак
«-» имеет то же значение, что и в случае формулы (66.1). Обозначив момент
инерции маятника относительно оси, проходящей через точку подвеса, буквой lможно написать:
(67.2) |

Рис.
170.
В случае малых колебаний (67.2) переходит в уже известное
нам уравнение:
(67.3) |
Через обозначена в данном случае следующая
величина:
(67.4) |
Из уравнений (67.3) и (67.4) следует, что при малых
отклонениях от положения равновесия физический маятник совершает гармонические
колебания, частота которых зависит от массы маятника, момента инерции маятника
относительно оси вращения и расстояния между осью вращения и центром инерции
маятника. В соответствии с (67.4) период колебания физического маятника
определяется выражением
(67.5) |
Из сопоставления формул (66.6) и (67.5) получается, что
математический маятник с длиной
(67.6) |
будет иметь такой период колебаний,
как и данный физический маятник. Величину (67.6) называют приведенной длиной
физического маятника. Таким образом, приведенная длина физического маятника —
это длина такого математического маятника, период колебаний которого совпадает
с периодом данного физического маятника
Точка на прямой, соединяющей точку подвеса с центром
инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром
качания физического маятника (см. точку О’ на рис.107).
По теореме Штейпера момент инерции маятника l может быть
представлен в виде
(67.7) |
где l0 — момент инерции
относительно оси, параллельной оси вращений и проходящей через центр инерции
маятника. Подставив (67.7) в формулу (67.6), получаем:
(67.8) |
Из (67.8) следует, что приведенная длина всегда больше 1,
так что точка подвеса и центр качания лежат по разные стороны от центра
инерции.
Подвесим маятник в точке, совпадающей с центром качания О’ В
соответствии с (67.8) приведенная длина в этом случае будет равна
(67.9) |
где l’ — расстояние между
первоначальным центром качания и центром инерции маятника. Учитывая, что , выражение (07.9)
можно записать следующим образом:
Выражение, стоящее в квадратных скобках, равно нулю.
Действительно, равно
I—моменту инерции относительно первоначальной оси
вращения; этой же величине в соответствии с (67.6) равно выражение mllпр. Таким образом, мы приходим к выводу,
что при подвешивании маятника в центре качания приведенная длина, а значит, и
период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и
центр качания обладают свойством взаимности при переносе точки подвеса в центр
качания прежняя точка подвеса .становится новым центром качания.
На установленном нами свойстве взаимности основано
определение ускорения силы тяжести с помощью так называемого оборотного
маятника. Оборотным называется такой маятник, у которого имеются две
параллельные друг другу, закрепленные вблизи его концов опорные призмы, за
которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и
закрепляться на нем тяжёлые грузы. Перемещением грузов добиваются того, чтобы
при подвешивании маятника за любую из призм период колебаний был одинаков.
Тогда расстояние между опорными ребрами призм будет равно lпр.
Измерив период колебаний маятника и зная l™, можно по Формуле
найти ускорение силы тяжести g.
Источник
