Каким свойством обладает цепь из элементов
Электромагнитные процессы, протекающие
в электротехнических устройствах, как правило, достаточно сложны. Однако во
многих случаях, их основные характеристики можно описать с помощью таких интегральных
понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе
совокупность электротехнических устройств, состоящую из соответствующим образом
соединенных источников и приемников электрической энергии, предназначенных для
генерации, передачи, распределения и преобразования электрической энергии и
(или) информации, рассматривают как электрическую цепь. Электрическая
цепь состоит из отдельных частей (объектов), выполняющих определенные функции
и называемых элементами цепи. Основными элементами цепи являются источники
и приемники электрической энергии (сигналов). Электротехнические устройства,
производящие электрическую энергию, называются генераторами или источниками
электрической энергии, а устройства, потребляющие ее – приемниками
(потребителями) электрической энергии.
У каждого элемента цепи можно выделить
определенное число зажимов (полюсов), с помощью которых он соединяется
с другими элементами. Различают двух –и многополюсные элементы.
Двухполюсники имеют два зажима. К ним относятся источники энергии (за исключением
управляемых и многофазных), резисторы, катушки индуктивности, конденсаторы.
Многополюсные элементы – это, например, триоды, трансформаторы, усилители и
т.д.
Все элементы электрической цепи условно
можно разделить на активные и пассивные. Активным называется элемент,
содержащий в своей структуре источник электрической энергии. К пассивным относятся
элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности
и конденсаторы) энергия. К основным характеристикам элементов цепи относятся
их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые
дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются
линейными дифференциальными или алгебраическими уравнениями, то они называются
линейными, в противном случае они относятся к классу нелинейных.
Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их
как линейных, что существенно упрощает математическое описание и анализ процессов,
определяется границами изменения характеризующих их переменных и их частот.
Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях,
называются параметрами элемента.
Если параметры элемента не являются функциями
пространственных координат, определяющих его геометрические размеры, то он называется
элементом с сосредоточенными параметрами. Если элемент описывается уравнениями,
в которые входят пространственные переменные, то он относится к классу элементов
с распределенными параметрами. Классическим примером последних является
линия передачи электроэнергии (длинная линия).
Цепи, содержащие только линейные элементы,
называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит
ее к классу нелинейных.
Рассмотрим пассивные элементы цепи, их
основные характеристики и параметры.
1. Резистивный элемент (резистор)
Условное графическое изображение резистора приведено на рис. 1,а. Резистор
– это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее
определяется геометрическими размерами тела и свойствами материала: удельным
сопротивлением r (Ом´
м) или обратной величиной – удельной проводимостью
(См/м).
В простейшем случае проводника длиной
и сечением S его сопротивление определяется выражением
.
В общем случае
определение сопротивления связано с расчетом поля в проводящей среде, разделяющей
два электрода.
Основной характеристикой резистивного элемента является зависимость
(или ),
называемая вольт-амперной характеристикой (ВАХ). Если зависимость
представляет собой прямую линию, проходящую через начало координат (см.рис.
1,б), то резистор называется линейным и описывается соотношением
или
,
где –
проводимость. При этом R=const.
Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет
показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими
параметрами. В частности безынерционному резистору ставятся в соответствие статическое
и дифференциальное
сопротивления.
2. Индуктивный элемент (катушка индуктивности)
Условное графическое изображение катушки индуктивности приведено на рис. 2,а.
Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета
индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
Индуктивность определяется отношением потокосцепления к току, протекающему
по виткам катушки,
.
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего
витки, на число этих витков ,
где .
Основной характеристикой катушки индуктивности является зависимость ,
называемая вебер-амперной характеристикой. Для линейных катушек индуктивности
зависимость
представляет собой прямую линию, проходящую через начало координат (см. рис.
2,б); при этом
.
Нелинейные свойства катушки индуктивности (см. кривую
на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала,
для которого зависимость
магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного
гистерезиса нелинейная катушка характеризуется статической
и дифференциальной
индуктивностями.
3. Емкостный элемент (конденсатор)
Условное графическое изображение конденсатора приведено на рис. 3,а.
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета
последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется
отношением заряда q на обкладках конденсатора к напряжению u между ними
и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними.
Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная
диэлектрическая проницаемость
=const. В этом случае зависимость
представляет собой прямую линию, проходящую через начало координат, (см. рис.
3,б) и
.
У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость
является функцией напряженности поля, что обусловливает нелинейность зависимости
(рис.
3,б). В этом случае без учета явления электрического гистерезиса нелинейный
конденсатор характеризуется статической
и дифференциальной
емкостями.
Схемы замещения источников электрической энергии
Свойства источника электрической энергии описываются ВАХ ,
называемой внешней характеристикой источника. Далее в этом разделе для
упрощения анализа и математического описания будут рассматриваться источники
постоянного напряжения (тока). Однако все полученные при этом закономерности,
понятия и эквивалентные схемы в полной мере распространяются на источники переменного
тока. ВАХ источника может быть определена экспериментально на основе схемы,
представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах
1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого
может изменяться с помощью переменного нагрузочного резистора (реостата) RН.
В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она
имеет две характерные точки, которые соответствуют:
а – режиму холостого хода ;
б – режиму короткого замыкания .
Для большинства источников режим короткого замыкания (иногда холостого хода)
является недопустимым. Токи и напряжения источника обычно могут изменяться в
определенных пределах, ограниченных сверху значениями, соответствующими номинальному
режиму (режиму, при котором изготовитель гарантирует наилучшие условия его
эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет
в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем
участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами
изменения напряжения и тока. Следует отметить, что многие источники (гальванические
элементы, аккумуляторы) имеют линейные ВАХ.
Прямая 2 на рис. 4,б описывается линейным уравнением
| , | (1) |
где – напряжение на зажимах
источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а);
– внутреннее
сопротивление источника.
Уравнение (1) позволяет составить последовательную схему замещения
источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый
идеальным источником ЭДС. Напряжение на зажимах этого элемента
не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б.
На основании (1) у такого источника .
Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.
Если ВАХ источника линейна, то для определения параметров
его схемы замещения необходимо провести замеры напряжения и тока для двух
любых режимов его работы.
Существует также параллельная схема замещения источника. Для ее описания разделим
левую и правую части соотношения (1) на .
В результате получим
или
| , | (2) |
где ;
– внутренняя
проводимость источника.
Уравнению (2) соответствует схема замещения источника на рис. 6,а.
На этой схеме символом J обозначен элемент, называемый идеальным источником
тока. Ток в ветви с этим элементом равен
и не зависит от напряжения на зажимах источника, следовательно, ему соответствует
ВАХ на рис. 6,б. На этом основании с учетом (2) у такого источника ,
т.е. его внутреннее сопротивление .
Отметим, что в расчетном плане при выполнении условия
последовательная и параллельная схемы замещения источника являются эквивалентными.
Однако в энергетическом отношении они различны, поскольку в режиме холостого
хода для последовательной схемы замещения мощность равна нулю, а для параллельной
– нет.
Кроме отмеченных режимов функционирования источника, на практике важное значение
имеет согласованный режим работы, при котором нагрузкой RН от источника
потребляется максимальная мощность
| , | (3) |
Условие такого режима
| , | (4) |
В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные
источники ЭДС и тока являются источниками бесконечно большой мощности.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия, 1972. –240 с. - Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е.
Учеб. пособие для электротехнических и энергетических специальностей вузов.
–М.: Высш. шк., 1972. –448 с.
Контрольные вопросы и задачи
- Может ли внешняя характеристик источника проходить через начало координат?
- Какой режим (холостой ход или короткое замыкание) является аварийным для
источника тока? - В чем заключаются эквивалентность и различие последовательной и параллельной
схем замещения источника? - Определить индуктивность L и энергию магнитного поля WМкатушки, если при
токе в ней I=20А потокосцепление y =2 Вб.Ответ: L=0,1 Гн; WМ=40 Дж.
- Определить емкость С и энергию электрического поля WЭконденсатора, если
при напряжении на его обкладках U=400 В заряд конденсатора q=0,2´
10-3 Кл.Ответ: С=0,5 мкФ; WЭ=0,04 Дж.
- У генератора постоянного тока при токе в нагрузке I1=50Анапряжение на зажимах
U1=210 В,а притоке, равном I2=100А, оно снижается до U2=190 В. - Определить параметры последовательной схемы замещения источника и ток короткого
замыкания.Ответ:
- Вывести соотношения (3) и (4) и определить максимальную мощность, отдаваемую
нагрузке, по условиям предыдущей задачи.Ответ:
Источник
 Ýëåìåíòîì ýëåêòðè÷åñêîé öåïè íàçûâàþò èäåàëèçèðîâàííîå óñòðîéñòâî, îòîáðàæàþùåå êàêîå-ëèáî èç ñâîéñòâ ðåàëüíîé ýëåêòðè÷åñêîé öåïè.
Ýëåìåíòîì ýëåêòðè÷åñêîé öåïè íàçûâàþò èäåàëèçèðîâàííîå óñòðîéñòâî, îòîáðàæàþùåå êàêîå-ëèáî èç ñâîéñòâ ðåàëüíîé ýëåêòðè÷åñêîé öåïè.
Ýëåêòðè÷åñêèå öåïè, â êîòîðûõ ïàðàìåòðû âñåõ ýëåìåíòîâ íå çàâèñÿò îò âåëè÷èíû è íàïðàâëåíèé òîêîâ è íàïðÿæåíèé, ò.å. ãðàôèêè âîëüò-àìïåðíûõ õàðàêòåðèñòèê (ÂÀÕ) ýëåìåíòîâ ÿâëÿþòñÿ ïðÿìûìè ëèíèÿìè, íàçûâàþòñÿ ëèíåéíûìè. Ñîîòâåòñòâåííî òàêèå ýëåìåíòû íàçûâàþòñÿ ëèíåéíûìè.
Êîãäà ïàðàìåòðû ýëåìåíòîâ ýëåêòðè÷åñêîé öåïè ñóùåñòâåííî çàâèñÿò îò òîêà èëè íàïðÿæåíèÿ, ò.å. ãðàôèêè ÂÀÕ ýòèõ ýëåìåíòîâ èìåþò êðèâîëèíåéíûé õàðàêòåð, òî òàêèå ýëåìåíòû íàçûâàþò íåëèíåéíûìè.
Åñëè ýëåêòðè÷åñêàÿ öåïü ñîäåðæèò õîòÿ áû îäèí íåëèíåéíûé ýëåìåíò, òî îíà ÿâëÿåòñÿ íåëèíåéíîé ýëåêòðè÷åñêîé öåïüþ.
 òåîðèè ýëåêòðè÷åñêèõ öåïåé ðàçëè÷àþò àêòèâíûå è ïàññèâíûå ýëåìåíòû. Ïåðâûå âíîñÿò ýíåðãèþ â ýëåêòðè÷åñêóþ öåïü, à âòîðûå åå ïîòðåáëÿþò.
Ïàññèâíûå ýëåìåíòû ýëåêòðè÷åñêèõ öåïåé
Ðåçèñòèâíûì ñîïðîòèâëåíèåì íàçûâàåòñÿ èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, îáëàäàþùèé ñâîéñòâîì íåîáðàòèìîãî ðàññåèâàíèÿ ýíåðãèè. Ãðàôè÷åñêîå èçîáðàæåíèå ýòîãî ýëåìåíòà è åãî âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà ïîêàçàíà íà ðèñóíêå (à – íåëèíåéíîå ñîïðîòèâëåíèå, á -ëèíåéíîå ñîïðîòèâëåíèå).
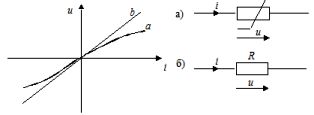
Íàïðÿæåíèå è òîê íà ðåçèñòèâíîì ñîïðîòèâëåíèè ñâÿçàíû ìåæäó ñîáîé çàâèñèìîñòÿìè: u = iR, i = Gu. Êîýôôèöèåíòû ïðîïîðöèîíàëüíîñòè R è G â ýòèõ ôîðìóëàõ íàçûâàþòñÿ ñîîòâåòñòâåííî ñîïðîòèâëåíèåì è ïðîâîäèìîñòüþ è èçìåðÿþòñÿ â îìàõ [Îì] è ñèìåíñàõ [Ñì]. R = 1/G.
Èíäóêòèâíûì ýëåìåíòîì íàçûâàåòñÿ èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, îáëàäàþùèé ñâîéñòâîì íàêîïëåíèÿ èì ýíåðãèè ìàãíèòíîãî ïîëÿ. Ãðàôè÷åñêîå èçîáðàæåíèå ýòîãî ýëåìåíòà ïîêàçàíî íà ðèñóíêå (à – íåëèíåéíîãî, á – ëèíåéíîãî).
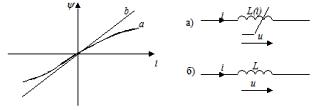
Ëèíåéíàÿ èíäóêòèâíîñòü õàðàêòåðèçóåòñÿ ëèíåéíîé çàâèñèìîñòüþ ìåæäó ïîòîêîñöåïëåíèåì ψ è òîêîì i, íàçûâàåìîé âåáåð-àìïåðíîé õàðàêòåðèñòèêîé ψ = Li. Íàïðÿæåíèå è òîê ñâÿçàíû ñîîòíîøåíèåì u = dψ/dt = L(di/dt)
Êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè L â ôîðìóëå è íàçûâàåòñÿ èíäóêòèâíîñòüþ è èçìåðÿåòñÿ â ãåíðè (Ãí).
Åìêîñòíûì ýëåìåíòîì (åìêîñòüþ) íàçûâàåòñÿ èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, îáëàäàþùèé ñâîéñòâîì íàêàïëèâàíèÿ ýíåðãèè ýëåêòðè÷åñêîãî ïîëÿ. Ãðàôè÷åñêîå èçîáðàæåíèå ýòîãî ýëåìåíòà ïîêàçàíî íà ðèñóíêå. (à – íåëèíåéíîãî, á – ëèíåéíîãî).
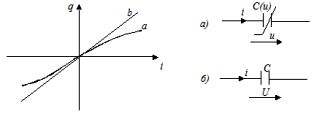
Ëèíåéíàÿ åìêîñòü õàðàêòåðèçóåòñÿ ëèíåéíîé çàâèñèìîñòüþ ìåæäó çàðÿäîì è íàïðÿæåíèåì, íàçûâàåìîé êóëîí-âîëüòîâîé õàðàêòåðèñòèêîé q = Cu
Íàïðÿæåíèå è òîê åìêîñòè ñâÿçàíû ñîîòíîøåíèÿìè i = dq/dt =C(du/dt).
Àêòèâíûå ýëåìåíòû ýëåêòðè÷åñêèõ öåïåé
Àêòèâíûìè íàçûâàþòñÿ ýëåìåíòû öåïè, êîòîðûå îòäàþò ýíåðãèþ â öåïü, ò.å. èñòî÷íèêè ýíåðãèè. Ñóùåñòâóþò íåçàâèñèìûå è çàâèñèìûå èñòî÷íèêè. Íåçàâèñèìûå èñòî÷íèêè: èñòî÷íèê íàïðÿæåíèÿ è èñòî÷íèê òîêà.
Èñòî÷íèê íàïðÿæåíèÿ – èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, íàïðÿæåíèå íà çàæèìàõ êîòîðîãî íå çàâèñèò îò ïðîòåêàþùåãî ÷åðåç íåãî òîêà.
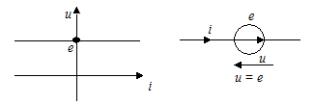
Âíóòðåííåå ñîïðîòèâëåíèå èäåàëüíîãî èñòî÷íèêà íàïðÿæåíèÿ ðàâíî íóëþ.
Èñòî÷íèê òîêà ýòî èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, òîê êîòîðîãî íå çàâèñèò îò íàïðÿæåíèÿ íà åãî çàæèìàõ.
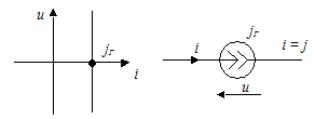
Âíóòðåííåå ñîïðîòèâëåíèå èäåàëüíîãî èñòî÷íèêà òîêà ðàâíî áåñêîíå÷íîñòè.
Èñòî÷íèêè íàïðÿæåíèÿ (òîêà) íàçûâàþòñÿ çàâèñèìûìè (óïðàâëÿåìûìè), åñëè âåëè÷èíà íàïðÿæåíèÿ (òîêà) èñòî÷íèêà çàâèñèò îò íàïðÿæåíèÿ èëè òîêà äðóãîãî ó÷àñòêà öåïè. Çàâèñèìûìè èñòî÷íèêàìè ìîäåëèðóþòñÿ ýëåêòðîííûå ëàìïû, òðàíçèñòîðû, óñèëèòåëè, ðàáîòàþùèå â ëèíåéíîì ðåæèìå.
Ðàçëè÷àþò ÷åòûðå òèïà çàâèñèìûõ èñòî÷íèêîâ.
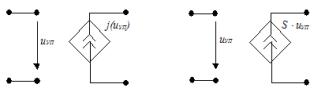
1. ÈÍÓÍ èñòî÷íèê íàïðÿæåíèÿ, óïðàâëÿåìûé íàïðÿæåíèåì: à) íåëèíåéíûé, á) ëèíåéíûé, μ êîýôôèöèåíò óñèëåíèÿ íàïðÿæåíèÿ
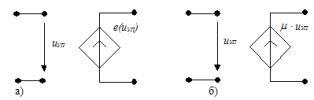
2. ÈÍÓÒ – èñòî÷íèê íàïðÿæåíèÿ, óïðàâëÿåìûé òîêîì: à) íåëèíåéíûé, á) ëèíåéíûé, γí ïåðåäàòî÷íîå ñîïðîòèâëåíèå
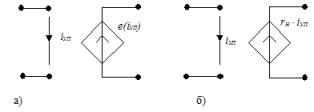
3. ÈÒÓÒ èñòî÷íèê òîêà, óïðàâëÿåìûé òîêîì: à) íåëèíåéíûé, á) ëèíåéíûé, β – êîýôôèöèåíò óñèëåíèÿ òîêà
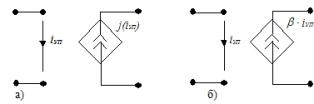
4. ÈÒÓÍ èñòî÷íèê òîêà, óïðàâëÿåìûé íàïðÿæåíèåì: à) íåëèíåéíûé, á) ëèíåéíûé, S – êðóòèçíà (ïåðåäàòî÷íàÿ ïðîâîäèìîñòü)
Источник
Ýëåìåíòû öåïè – ýòî òàêèå èäåàëèçèðîâàííûå óñòðîéñòâà â ýëåêòðè÷åñêîé öåïè, êîòîðûå îòîáðàæàþò êàêîå-ëèáî èç ñâîéñòâ ðåàëüíîé ýëåêòðè÷åñêîé öåïè. Åñëè â ýëåêòðè÷åñêèõ öåïÿõ îò íàïðàâëåíèé è âåëè÷èí íàïðÿæåíèé, à òàêæå òîêîâ íå çàâèñÿò ïàðàìåòðû âñåõ ýëåìåíòîâ, òî åñòü ïðÿìûìè ëèíèÿìè ÿâëÿþòñÿ ãðàôèêè âîëüò-àìïåðíûõ õàðàêòåðèñòèê (ÂÀÕ), òî òàêèå ýëåêòðè÷åñêèå öåïè íàçûâàþòñÿ ëèíåéíûìè.
Êîãäà æå ñóùåñòâóåò çàâèñèìîñòü ïàðàìåòðîâ ýëåìåíòîâ ýëåêòðè÷åñêîé öåïè îò íàïðÿæåíèÿ èëè òîêà, ãðàôèêè ÂÀÕ ýòèõ ýëåìåíòîâ áóäóò èìåòü êðèâîëèíåéíûé õàðàêòåð, òî òàêèå ýëåìåíòû öåïè íàçûâàþòñÿ íåëèíåéíûìè.
Íåëèíåéíîé ýëåêòðè÷åñêîé öåïüþ ÿâëÿåòñÿ ñîäåðæàùàÿ õîòÿ áû îäèí èç íåëèíåéíûõ ýëåìåíòîâ ýëåêòðè÷åñêàÿ öåïü. Ðàçëè÷àþòñÿ â òåîðèè ýëåêòðè÷åñêèõ öåïåé ïàññèâíûå è àêòèâíûå ýëåìåíòû öåïè. Ïàññèâíûå ýëåìåíòû ïîòðåáëÿþò ýíåðãèþ â ýëåêòðè÷åñêîé öåïè, êîòîðóþ â íåå âíîñÿò àêòèâíûå ýëåìåíòû.
Ïàññèâíûå ýëåìåíòû öåïè.
Îáëàäàþùèé ñâîéñòâîì íåîáðàòèìîãî ðàññåèâàíèÿ ýíåðãèè èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè íàçûâàåòñÿ ðåçèñòèâíûì ñîïðîòèâëåíèåì.
Âîëüò-àìïåðíàÿ õàðàêòåðèñòèêà è åãî ãðàôè÷åñêîå èçîáðàæåíèå äàííîãî ýëåìåíòà ïîêàçàíû íà ðèñóíêå.

Ñâÿçàíû ìåæäó ñîáîé òîê è íàïðÿæåíèå íà ðåçèñòèâíîì ñîïðîòèâëåíèè ñëåäóþùèìè çàâèñèìîñòÿìè: u = iR, i = Gu. Â äàííûõ ôîðìóëàõ êîýôôèöèåíòû ïðîïîðöèîíàëüíîñòè R (ñîïðîòèâëåíèå) è G (ïðîâîäèìîñòü) èçìåðÿþòñÿ â îìàõ [Îì] è ñèìåíñàõ [Ñì]:
R = 1/G
Èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, êîòîðûé èìååò ñâîéñòâî íàêàïëèâàòü ýíåðãèþ ìàãíèòíîãî ïîëÿ íàçûâàåòñÿ èíäóêòèâíûì ýëåìåíòîì.
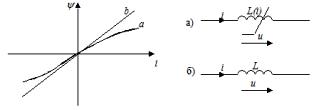
Ëèíåéíîé çàâèñèìîñòüþ ìåæäó òîêîì i è ïîòîêîñöåïëåíèåì ψ õàðàêòåðèçóåòñÿ ëèíåéíàÿ èíäóêòèâíîñòü, ïîëó÷èâøàÿ íàçâàíèå âåáåð-àìïåðíàÿ õàðàêòåðèñòèêà ψ = Li.
Ñîîòíîøåíèåì u = dψ/dt = L(di/dt), ñâÿçûâàþòñÿ ìåæäó ñîáîé òîê è íàïðÿæåíèå.
 äàííîé ôîðìóëå êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè L è íàçûâàåòñÿ èíäóêòèâíîñòüþ, åäèíèöåé åãî èçìåðåíèÿ ÿâëÿåòñÿ ãåíðè (Ãí).
Èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè íàçûâàåòñÿ åìêîñòíûì ýëåìåíòîì (åìêîñòüþ), åñëè îí îáëàäàåò ñâîéñòâîì íàêàïëèâàòü ýíåðãèþ ýëåêòðè÷åñêîãî ïîëÿ.

Êóëîí-âîëüòíîé õàðàêòåðèñòèêîé q = Cu íàçûâàåòñÿ ëèíåéíàÿ çàâèñèìîñòü ìåæäó çàðÿäîì è íàïðÿæåíèåì, õàðàêòåðèçóþùàÿñÿ ëèíåéíîé åìêîñòüþ. Ñâÿçàíû òîê è íàïðÿæåíèå åìêîñòè ñîîòíîøåíèÿìè:
i = dq/dt =C(du/dt).
Àêòèâíûå ýëåìåíòû öåïè.
Ýëåìåíòû öåïè, îòäàþùèå ýíåðãèþ â öåïü, ñ÷èòàþùèåñÿ èñòî÷íèêàìè ýíåðãèè íàçûâàþòñÿ àêòèâíûìè ýëåìåíòàìè. Ðàçëè÷àþòñÿ çàâèñèìûå è íåçàâèñèìûå èñòî÷íèêè ýíåðãèè. Ê íåçàâèñèìûì îòíîñÿòñÿ èñòî÷íèê òîêà è èñòî÷íèê íàïðÿæåíèÿ.
Ïîä èñòî÷íèêîì íàïðÿæåíèÿ ïîäðàçóìåâàåòñÿ èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, íàïðÿæåíèå íà çàæèìàõ êîòîðîãî íå èìååò çàâèñèìîñòè îò ïðîòåêàþùåãî ÷åðåç íåãî òîêà.

Ó èäåàëüíîãî èñòî÷íèêà íàïðÿæåíèÿ ðàâíî íóëþ âíóòðåííåå ñîïðîòèâëåíèå.
Èäåàëèçèðîâàííûé ýëåìåíò ýëåêòðè÷åñêîé öåïè, îò íàïðÿæåíèÿ íà åãî çàæèìàõ òîê êîòîðîãî íå çàâèñèò, íàçûâàåòñÿ èñòî÷íèêîì òîêà.

 èäåàëüíîì èñòî÷íèêå òîêà âíóòðåííå ñîïðîòèâëåíèå ðàâíî áåñêîíå÷íîñòè.
Åñëè âåëè÷èíà òîêà (íàïðÿæåíèÿ) çàâèñèò îò òîêà èëè íàïðÿæåíèÿ äðóãîãî ó÷àñòêà öåïè, òî òàêèå èñòî÷íèêè òîêà (íàïðÿæåíèÿ) íàçûâàþòñÿ çàâèñèìûìè (óïðàâëÿåìûìè). Òðàíçèñòîðû, ýëåêòðîííûå ëàìïû, ðàáîòàþùèå â ëèíåéíîì ðåæèìå óñèëèòåëè ìîäåëèðóþòñÿ çàâèñèìûìè èñòî÷íèêàìè.
Ñóùåñòâóåò ÷åòûðå òèïà çàâèñèìûõ èñòî÷íèêîâ:
1. Èñòî÷íèê íàïðÿæåíèÿ, óïðàâëÿåìûé íàïðÿæåíèåì (ÈÍÓÍ) – à) íåëèíåéíûé, á) ëèíåéíûé, μ – êîýôôèöèåíò óñèëåíèÿ íàïðÿæåíèÿ

2. ÈÍÓÍ – à) íåëèíåéíûé, á) ëèíåéíûé, γí – ïåðåäàòî÷íîå ñîïðîòèâëåíèå
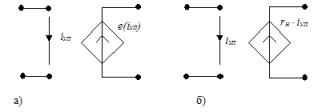
3. ÈÍÓÍ – à) íåëèíåéíûé, á) ëèíåéíûé, β – êîýôôèöèåíò óñèëåíèÿ òîêà

4. ÈÍÓÍ – à) íåëèíåéíûé, á) ëèíåéíûé, S – êðóòèçíà (ïåðåäàòî÷íàÿ ïðîâîäèìîñòü).

Источник
