Каким свойством обладает любой прямоугольник
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
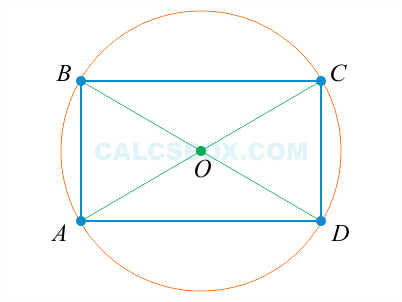
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 – b2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Источник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ), ( angle B = angle D ))
2. Противоположные стороны равны
( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны
( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу
( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны
( AC = BD )

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ).
Следовательно, ( triangle ABD = triangle DCA ) по двум катетам (( AB = CD ) и ( AD ) — совместный).
Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.
Значит, ( AC = BD ).
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
( Rightarrow AB = CD ), ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.
Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ), ( angle B = angle D ).
Выводим, что ( angle A = angle B = angle C = angle D ). Все они по ( 90^{circ} ). В сумме — ( 360^{circ} ).
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
( AC^2=AD^2+CD^2 )
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

8. Точка пересечения диагоналей делит их пополам
( AO = BO = CO = DO )

9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности

10. Сумма всех углов равна 360 градусов
( angle ABC + angle BCD + angle CDA + angle DAB = 360^{circ} )
11. Все углы прямоугольника прямые
( angle ABC = angle BCD = angle CDA = angle DAB = 90^{circ} )

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна ( 180^{circ} )
( angle ABC = angle CDA = 180^{circ},enspace angle BCD = angle DAB = 180^{circ} )
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
Узнать стоимость
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами.
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб — это параллелограмм, у которого все стороны равны.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Источник
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это…
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
Судите сами:
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У прямоугольника равны противоположные стороны.
- У прямоугольника противоположные стороны параллельны.
- У прямоугольников все прилегающие друг к другу стороны пересекаются под прямыми углами. А в сумме они дают 360 градусов.
- У прямоугольников обе диагонали равны между собой.
- Диагональ прямоугольника делит фигуру ровно пополам, и в результате получаются два одинаковых прямоугольных треугольника.
- Диагонали прямоугольника пересекаются в его геометрическом центре. А их точка пересечения делит каждую диагональ на два равных отрезка. Более того, все четыре отрезка равны между собой.
- У прямоугольника точка пересечения диагоналей является еще и центром описанной вокруг окружности. Причем длина диагонали одновременна является диаметром (что это такое?) этой окружности.
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
- ВоркЗилла – удаленная работа для всех
- Анкетка – платят за прохождение тестов
- Etxt – платят за написание текстов
- Кьюкоммент – биржа комментариев
- Поиск лучшего курса обмена
- 60сек – выгодный обмен криптовалют
- Бинанс – надёжная биржа криптовалют
- ВкТаргет – заработок в соцсетях (ВК, ОК, FB и др.)
Источник
Прямоугольник.
Приступаем к изучению разных видов параллелограмма.
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.

– прямоугольник
Поскольку прямоугольник – это параллелограмм, то он обладаем теми же свойствами, что и параллелограмм. Кроме того, у него есть ещё свои, особые свойства.
Рассмотрим эти свойства.
ТЕОРЕМА (СВОЙСТВО I). У прямоугольника диагонали равны.

Дано: – прямоугольник,
и – диагонали.
Доказать:
Доказательство.
1. Рассмотрим и .
по признаку равенства прямоугольных треугольников (или по I признаку равенства треугольников) все соответствующие стороны и углы у этих треугольников равны, т.е. , ч.т.д.
ТЕОРЕМА (СВОЙСТВО II). У прямоугольника каждая диагональ делит его на два равных прямоугольных треугольника.

Дано: – прямоугольник,
– диагональ.
Доказать:
Доказательство.
Рассмотрим и .
по III признаку равенства треугольников. по определению прямоугольника. Значит, треугольники и – равные и прямоугольные, ч.т.д.
Итак, прямоугольник обладает следующими свойствами:
У прямоугольника противолежащие стороны и углы равны.
У прямоугольника диагонали пересекаются и точкой пересечения делятся пополам.
У прямоугольника диагонали равны.
У прямоугольника каждая диагональ делит его на два равных прямоугольных треугольника.
Стороны прямоугольника являются его высотами.
Выясним теперь, по каким признакам можно утверждать, что геометрическая фигура является прямоугольником.
ТЕОРЕМА (ПРИЗНАК I). Если у четырёхугольника три угла прямые, то такой четырёхугольник является прямоугольником.
Дано: – четырёхугольник,
Доказать: – прямоугольник.
Доказательство.
Данный четырёхугольник будет прямоугольником, если мы докажем, что четвёртый угол также равен .
1. Так как , то . Так как , то .
2. по признаку параллельности прямых.
3. по признаку параллельности прямых.
4. Значит, – параллелограмм (по определению). По свойству углов параллелограмма, .
5. Итак, – параллелограмм, у которого все углы прямые. По определению, такой параллелограмм является прямоугольником, ч.т.д.
ТЕОРЕМА (ПРИЗНАК II). Если у параллелограмма диагонали равны, то такой параллелограмм является прямоугольником.

Дано: – параллелограмм,
– диагонали.
Доказать: – прямоугольник.
Доказательство.
Данный параллелограмм будет прямоугольником, если мы докажем, что у него все углы равны .
1. Рассмотрим и .
по III признаку равенства прямоугольных треугольников, следовательно, .
2. Так как – параллелограмм, то у него стороны попарно параллельны, т.е. . и – внутренние односторонние при параллельных прямых, значит, по свойству параллельных прямых, . Учитывая доказанное равенство этих углов, получаем, что .
3. По свойству углов параллелограмма, и .
4. Итак, у параллелограмма все углы прямые, значит, он является прямоугольником (по определению), ч.т.д.
ТЕОРЕМА (ПРИЗНАК III). Если у параллелограмма один угол прямой, то такой параллелограмм является прямоугольником.
Дано: – параллелограмм,
.
Доказать: – прямоугольник.
Доказательство.
Данный параллелограмм будет прямоугольником, если мы докажем, что у него все углы равны .
1. Т.к. – параллелограмм, то по определению, т.е. и .
По свойству углов параллелограмма, .
2. и – внутренние односторонние при параллельных прямых, значит, по свойству параллельных прямых, .
3. Т.к. , то .
4. Итак, , значит, по определению, параллелограмм является прямоугольником, ч.т.д.
Периметр прямоугольника равен см, а одна из его сторон меньше другой на см. Найдите меньшую сторону прямоугольника.
В прямоугольнике один из углов, образованных диагоналями, равен . Меньшая сторона прямоугольника равна см. Найдите диагональ прямоугольника.
В прямоугольнике перпендикуляры, проведённые из точки пересечения диагоналей к его сторонам, равны соответственно см и см. Найдите периметр прямоугольника.
В прямоугольнике диагональ составляет со стороной угол, равный . Найдите больший угол между диагоналями прямоугольника.

В прямоугольнике один из углов, образованных диагоналями, равен . Диагонали прямоугольника равны см. Найдите меньшую сторону прямоугольника.
В прямоугольнике диагонали пересекаются в точке . Точка – середина стороны . Найдите .
В прямоугольнике диагонали пересекаются в точке . Отрезок является высотой треугольника . Найдите .
В параллелограмме с острым углом диагонали пересекаются в точке . На отрезках и взяты точки и соответственно, . Докажите, что четырёхугольник является прямоугольником.
В прямоугольнике – точка пересечения диагоналей, и – высоты треугольников и соответственно, см. Найдите .
В четырёхугольнике диагонали пересекаются в точке . Найдите .
В прямоугольнике – точка пересечения диагоналей, и – перпендикуляры, проведённые из вершин и к прямой . Известно, что . Найдите .
В четырёхугольнике диагонали пересекаются в точке , . Найдите .
В прямоугольнике точки и – середины сторон и соответственно. На прямой взята точка , на прямой – точка . Известно, что . Найдите отношение сторон .
На основании равнобедренного треугольника взята точка , а на сторонах и – соответственно точки и , . Найдите .
В прямоугольнике – точка пересечения диагоналей. Точки и – середины сторон и соответственно. Точка делит отрезок в отношении , считая от точки Найдите отношение .
Некая прямая, параллельная основанию равнобедренного треугольника , пересекает стороны и в отношении , считая от точки . Найдите .
На диагонали прямоугольника взята точка . Известно, что . Докажите, что .
Дан параллелограмм с острым углом . На отрезке , как на диаметре построена окружность, которая пересекает луч в точке , лежащей вне параллелограмма. . Найдите расстояние между прямыми и , если см.
На отрезках и в прямоугольнике взяты точки и соответственно, . Докажите, что .
Дан параллелограмм с тупым углом . На диагонали , как на диаметре, построена окружность, пересекающая отрезок в точке – перпендикуляр к прямой . Найдите , если см.
Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону на отрезки равной длины. Найдите периметр этого прямоугольника, если длина меньшей стороны прямоугольника равна см.
Периметр прямоугольника равен см. Найдите сумму расстояний от произвольной внутренней точки прямоугольника до его сторон.
Постройте прямоугольник:
по двум сторонам, имеющим общую вершину;
по стороне и диагонали;
по диагонали и углу между диагоналями;
по диагонали и сумме прилежащих сторон.
Диагональ прямоугольника равна см. Найдите медиану треугольника , проведённую к его большей стороне.
Найдите острый угол между диагоналями прямоугольника, если одна из них делит угол при вершине прямоугольника в отношении .
Периметр прямоугольника равен см. Найдите стороны прямоугольника, если одна из них в раз больше другой.
Периметр прямоугольника равен см. Найдите его стороны, если одна из них на см меньше другой.
Диагонали прямоугольника пересекаются в точке . Найдите угол между диагоналями, если .
В прямоугольнике проведена диагональ . Известно, что в 2 раза больше, чем . Чему равны эти углы?
Одна из сторон прямоугольника на см больше другой. Найдите стороны прямоугольника, если его периметр равен см.
Меньшая сторона прямоугольника см, угол между диагоналями равен . Найдите диагонали прямоугольника.
Дан прямоугольник – точка пересечения его диагоналей. Докажите, что и – равные равнобедренные треугольники.
Найдите диагонали прямоугольника, если его периметр равен см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен см.
Докажите, что отрезок, соединяющий точку пересечения диагоналей прямоугольника с серединой стороны, перпендикулярен этой стороне.
В прямоугольнике диагональ в раз больше стороны . Периметр треугольника равен см ( – точка пересечения диагоналей). Найдите длину диагонали .
Из точки , взятой на стороне прямоугольника , опущен перпендикуляр на сторону . Докажите, что четырёхугольник – прямоугольник.
Диагонали прямоугольника пересекаются в точке , его диагональ равна см. Найдите длины отрезков и .
Диагонали прямоугольника пересекаются в точке . Докажите, что .
Диагонали прямоугольника пересекаются в точке . Найдите стороны прямоугольника, если его периметр равен см, а периметры треугольников и равны см и см соответственно.
Дан прямоугольник – точка пересечения его диагоналей. Найдите периметр треугольника , если
Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
Диагонали прямоугольника пересекаются в точке , сторона равна см, диагональ равна см. Определите вид треугольника (ответ обоснуйте) и найдите его периметр.
В прямоугольнике биссектриса угла пересекает сторону в точке . Докажите, что треугольник – равнобедренный.
В прямоугольнике диагональ делит угол в отношении . Найдите углы треугольника ( – точка пересечения диагоналей).
Найдите диагональ прямоугольника, если его периметр равен см, а периметр одного из треугольников, на которые диагональ делит прямоугольник, равен см.
В прямоугольнике проведена биссектриса угла . Найдите периметр прямоугольника, если см, см.

Расстояния от точки пересечения диагоналей прямоугольника до его сторон равны см и см. Найдите большую сторону данного прямоугольника.
Диагонали прямоугольника пересекаются под углом . Найдите угол между диагональю прямоугольника и его меньшей стороной.
В прямоугольнике диагональ в два раза больше стороны . Найдите периметр треугольника , если расстояние от точки пересечения диагоналей прямоугольника до стороны равно см.
Диагонали прямоугольника пересекаются в точке , образуя тупой угол . Определите, какое расстояние больше: от точки до стороны или от точки до стороны .
В прямоугольном треугольнике ( – прямой) через точку , лежащую на гипотенузе, проведены прямые и , параллельные катетам и соответственно. Периметр треугольника равен см, а периметр треугольника равен см. Найдите периметр треугольника .

На стороне равностороннего треугольника взята точка так, что сумма расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
Периметр прямоугольника равен см, а его диагональ равна см. Найдите периметр треугольника .
Найдите периметр прямоугольника , если биссектрисы и углов и делят сторону на три отрезка, длина каждого из которых равна см.

Точка пересечения диагоналей прямоугольника отстоит от его сторон на расстояниях см и см. Найдите меньшую сторону данного прямоугольника.
В прямоугольнике диагональ в два раза больше стороны . Найдите острый угол между диагоналями прямоугольника.
Меньшая сторона прямоугольника равна см. Угол между его диагоналями равен . Вычислите длину диагонали прямоугольника.
Диагонали прямоугольника пересекаются в точке . Определите, какое расстояние больше: от точки до стороны или от точки до стороны , если сторона больше стороны .
В прямоугольнике через точку проведены прямая , параллельная сторонам и , и прямая , параллельная сторонами и . Периметр прямоугольника равен см, а периметр прямоугольника равен см. Найдите периметр прямоугольника .

На продолжении стороны равностороннего треугольника взята точка так, что разность расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
Диагонали прямоугольника пересекаются в точке . Периметр треугольника равен см, а периметр треугольника равен см. Найдите периметр треугольника , если диагональ прямоугольника равна см.
Найдите периметр прямоугольника , если биссектрисы и углов и делят сторону на три отрезка, длина каждого из которых равна см.

Сумма расстояний от точки пересечения диагоналей прямоугольника до всех его вершин равна см. Найдите диагональ данного прямоугольника.
Диагональ прямоугольника образует угол с одной из его сторон. Найдите острый угол между диагоналями прямоугольника.
Диагональ прямоугольника равна см. Угол между его диагоналями равен . Вычислите длину меньшей стороны прямоугольника.
Диагонали прямоугольника пересекаются в точке , образуя острый угол . Определите, какое расстояние больше: от точки до стороны или от точки до стороны .
В прямоугольном равнобедренном треугольнике ( – прямой) через точки и , лежащие на гипотенузе, проведены прямые и , параллельные катету , и прямые и , параллельные катету . Сравните периметры четырёхугольников и .

На основании равнобедренного треугольника взята точка так, что сумма расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
Диагонали прямоугольника пересекаются в точке . Периметр треугольника равен см, а сторона равна см. Найдите периметр треугольника .
Биссектрисы углов и прямоугольника пересекаются на стороне в точке . Найдите периметр прямоугольника, если длина равна см.

Сумма расстояний от точки пересечения диагоналей прямоугольника до всех его сторон равна см. Найдите периметр данного прямоугольника.
Угол между диагоналями прямоугольника равен . Найдите угол .
В прямоугольнике сторона в два раза меньше диагонали . Найдите расстояние от точки пересечения диагоналей прямоугольника до стороны , если периметр треугольника равен см.
Диагонали прямоугольника пересекаются в точке . Определите, какое расстояние больше: от точки до стороны или от точки до стороны , если сторона меньше стороны .
В прямоугольном равнобедренном треугольнике ( – прямой) через точку , лежащую на гипотенузе, проведены прямые и , параллельные катетам и соответ
