Каким свойством обладает окружность описывающая окружность
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
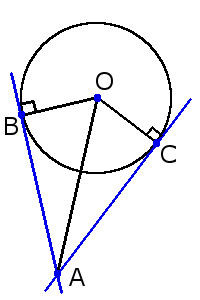
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
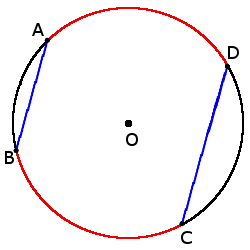
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
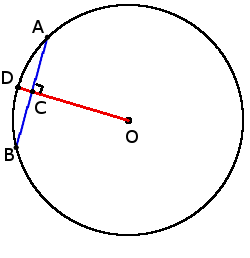
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
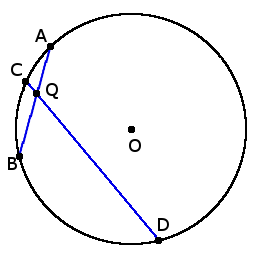
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
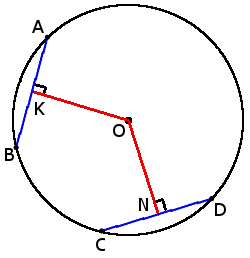
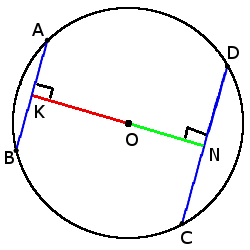
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK

6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
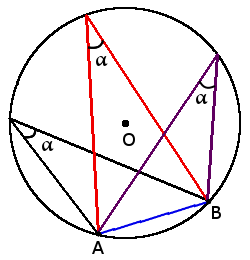
1. Все вписанные углы, которые опираются на одну дугу – равны.
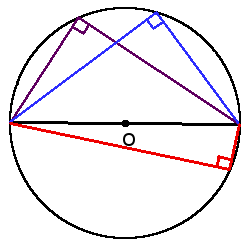
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
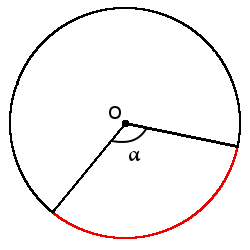
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника.
Что же это такое?
Читай статью и все поймешь!
Окружность, описанная около треугольника – это окружность, которая проходит через все три вершины этого треугольника.
- Вокруг всякого треугольника можно описать окружность.
Существование и центр описанной окружности
- Вокруг всякого треугольника можно описать окружность, при том единственным образом.
- Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус описанной окружности
- ( displaystyle frac{a}{sin angle A}=frac{b}{sin angle B}=frac{c}{sin angle C}=2R)
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
Центр окружности – внутри или снаружи
- В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника
- В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
- В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
НАЧАЛЬНЫЙ УРОВЕНЬ
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Вот так:
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.
Регистрируйся здесь и приходи!
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Но ведь треугольники-то бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта можешь найти в следующих уровнях теории, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая ( displaystyle a) – это серединный перпендикуляр к отрезку ( displaystyle AB).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), чтовсе три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке ( displaystyle O).
Это и есть центр описанной около (вокруг) треугольника ( displaystyle ABC) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
А вот еслиостроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда? Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:
( Large displaystyle frac{a}{sin angle A}=2R)
Ну и, конечно,
( displaystyle begin{array}{l}frac{b}{sin angle B}=2R\frac{c}{sin angle C}=2Rend{array})
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол. Хорошая формула? По-моему, просто отличная!
НРАВИТСЯ УЧЕБНИК?
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
СРЕДНИЙ УРОВЕНЬ
В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.
Окружность, описанная около треугольника, – такая окружность, что происходит через все три вершины этого треугольника.
Существование и центр описанной окружности
Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотри, вот так:
Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Зарегистрируйся один раз и ты откроешь все 100 статей учебника
А также получишь доступ к видеоурокам и другим бесплатным материалам курса “Подготовка к ЕГЭ с репетитором”
* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «( displaystyle X)» – такое множество точек, что все они обладают свойством «( displaystyle X)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «( displaystyle X)» – это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
1
Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
2
Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему
Приступим:
Проверим 1. Пусть точка ( displaystyle M) лежит на серединном перпендикуляре к отрезку ( displaystyle AB).
Соединим ( displaystyle M) с ( displaystyle A) и с ( displaystyle B).Тогда линия ( displaystyle MK) является медианой и высотой в ( displaystyle Delta AMB). Значит, ( displaystyle Delta AMB) – равнобедренный, ( displaystyle MA=MB) – убедились, что любая точка ( displaystyle M), лежащая на серединном перпендикуляре, одинаково удалена от точек ( displaystyle A) и ( displaystyle B).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка ( displaystyle M) равноудалена от точек ( displaystyle A) и ( displaystyle B), то есть ( displaystyle MA=MB).
Возьмём ( displaystyle K) – середину ( displaystyle AB) и соединим ( displaystyle M) и ( displaystyle K). Получилась медиана ( displaystyle MK). Но ( displaystyle Delta AMB) – равнобедренный по условию ( displaystyle (MA=MB)Rightarrow MK) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка ( displaystyle M) – точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник ( displaystyle ABC). Проведём два серединных перпендикуляра ( displaystyle {{a}_{1}}) и ( displaystyle {{a}_{2}}), скажем, к отрезкам ( displaystyle AB) и ( displaystyle BC). Они пересекутся в какой-то точке, которую мы назовем ( displaystyle O).
А теперь, внимание!
Точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{1}}Rightarrow OA=OB);
точка ( displaystyle O) лежит на серединном перпендикуляре ( displaystyle {{a}_{2}}Rightarrow OB=OC).
И значит, ( displaystyle OA=OB=OC) и ( displaystyle OA=OC).
Отсюда следует сразу несколько вещей:
Во-первых, ( displaystyle OA=OCRightarrow ) точка ( displaystyle O) обязана лежать на третьем серединном перпендикуляре, к отрезку ( displaystyle AC).
То есть серединный перпендикуляр ( displaystyle {{a}_{3}}) тоже обязан пройти через точку ( displaystyle O), и ( displaystyle Rightarrow ) все три серединных перпендикуляра пересеклись в одной точке.
Во-вторых, ( displaystyle OA=OB=OCRightarrow ), если мы проведём окружность с центром в точке ( displaystyle O) и радиусом ( displaystyle OA), то эта окружность также пройдёт и через точку ( displaystyle B), и через точку ( displaystyle C), то есть будет описанной окружностью ( displaystyle Delta ABC). Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.
И последнее: о единственности. Ясно (почти), что точку ( displaystyle O) можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» – оставим на твоё размышление.
Вот и доказали теорему. Можно кричать «Ура!».
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.
Регистрируйся здесь и приходи!
Радиус описанной окружности
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме).
( displaystyle frac{a}{sin angle A}=frac{b}{sin angle B}=frac{c}{sin angle C}=2R)
То есть:
( largedisplaystyle frac{text{a}}{sin angle text{A}}=2text{R}) и
( largedisplaystyle frac{text{b}}{sin angle text{B}}=2text{R}) и
( largedisplaystyle frac{text{c}}{sin angle text{C}}=2text{R}).
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол. И всё!
Центр окружности – внутри или снаружи
А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника.
Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.
И вообще:
В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника.
Втупоугольном треугольнике центр описанной окружности всегда лежитвне треугольника.
Впрямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
P.S. Анонс бесплатных вебинаров на 14-е февраля 2021
Математика. ЕГЭ 13. Тригонометрическая замена. Задача-оборотень.
14 февраля 2021, воскресенье, 11-00
Мы на курсе уже прошли тригонометрию и научились решать 13-е задачи. В этих задачах чаще всего нужно синус или косинус заменить какой-то буквой, и решать квадратное уравнение.
Но что если я вам скажу, что есть такие задачи, в которых всё наоборот – нужно обычный икс заменить на синус или косинус, хотя изначально там нет никакого намёка на тригонометрию?
Приходите на урок в ближайшее воскресенье, и увидите такую задачу-оборотня, а заодно – научитесь решать дичайшие иррациональные уравнения.
https://youclever.org/free-sunday-webinars/ – регистрация на вебинары.
Информатика. ЕГЭ 24. Решаем задачу 24 несколькими способами
14 февраля 2021, воскресенье, 12-30
Вот чем хорош язык Python? Ну в общем-то всем, конечно:) Но особенно нас при подготовке к ЕГЭ в нём порадует огромное количество встроенных функций и методов для работы с текстом. Ведь в ЕГЭ есть задача №24, в которой нужно анализировать огромный текст. Приходите на наш бесплатный вебинар в воскресенье – там мы разберём одну такую задачу несколькими способами – и вы выберете для себя, какие приёмы вам больше по душе.
https://youclever.org/free-sunday-webinars/ – регистрация на вебинары.
Зарегистрируйтесь один раз и вы будете получать приглашения на ВСЕ бесплатные вебинары до конца года.
Источник
