Каким свойством обладает параллелограмм
Определение.
Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Параллелограммы отличаются между собой как размером прилегающих сторон, так и углами, однако противоположные углы одинаковые.
Признаки параллелограмма
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
2. Четырехугольник имеет пару параллельных и равных сторон:
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Основные свойства параллелограмма
Квадрат, прямоугольник и ромб – есть параллелограммом.
1. Противоположные стороны параллелограмма имеют одинаковую длину:
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма одинаковые:
∠ABC = ∠CDA, ∠BCD = ∠DAB
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
6. Каждая диагональ делит параллелограмма на два равных треугольника
7. Две диагональ делят параллелограмм на две пары равных треугольников
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9. Точка пересечения диагоналей называется центром симметрии параллелограмма
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
a =
√d12 + d22 – 2d1d2·cosγ2 =
√d12 + d22 + 2d1d2·cosδ2
b =
√d12 + d22 + 2d1d2·cosγ2 =
√d12 + d22 – 2d1d2·cosδ2
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Определение.
Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.
Параллелограмм имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)
d1 = √a2 + b2 – 2ab·cosβ
d2 = √a2 + b2 + 2ab·cosβ
2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
d1 = √a2 + b2 + 2ab·cosα
d2 = √a2 + b2 – 2ab·cosα
3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:
d1 = √2a2 + 2b2 – d22
d2 = √2a2 + 2b2 – d12
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d1 = | 2S | = | 2S |
| d2·sinγ | d2·sinδ |
| d2 = | 2S | = | 2S |
| d1·sinγ | d1·sinδ |
Периметр параллелограмма
Определение.
Периметром параллелограмма называется сумма длин всех сторон параллелограмма.
Формулы определения длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали:
P = 2a + √2d12 + 2d22 – 4a2
P = 2b + √2d12 + 2d22 – 4b2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
Площадь параллелограмма
Определение.
Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.
Формулы определения площади параллелограмма:
1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:
S = a · ha
S = b · hb
2. Формула площади параллелограмма через две стороны и синус угла между ними:
S = ab sinα
S = ab sinβ
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
Источник
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a * h, где a — сторона, h — высота.
- S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
- S = 0,5 * (d1 * d2), где d1,d2 — две диагонали.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок математики в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
У нас есть отличные дополнительные занятия по математике! Для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма ABCD равны: AB = DC, BC = AD.
- Противоположные углы параллелограмма ABCD равны:∠A = ∠C, ∠B = ∠D.
- Диагонали параллелограмма ABCD равны и точкой пересечения делятся пополам: BO = OD, AO = OC.
- Диагональ делит параллелограмм ABCD на два равных треугольника: △ABC = △CDA.
- Сумма углов в параллелограмме ABCD, прилежащих к одной стороне, равна 180 градусам: ∠A + ∠D = 180°.
- В параллелограмме ABCD накрест лежащие углы при диагонали равны: ∠BAC = ∠ACD, ∠BCA = ∠CAD.
- В параллелограмме ABCD сумма всех углов равна 360° градусам.
- Точка пересечения диагоналей является центром симметрии параллелограмма ABCD.
- В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 * (a2 + b2 ).
- Биссектриса отсекает от параллелограмма ABCD равнобедренный треугольник.
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- Как противоположные стороны параллелограмма: AB = CD
- Как внутренние накрест лежащие равны пары углов: ∠1 = ∠2, ∠3 = ∠4.
- Следовательно, треугольник AOB равен треугольнику COD, из чего следует:
- CO = OA
- BO = DO
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2, как внутренние накрест лежащие углы для параллельных прямых.
Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Рассмотрим треугольники ABC и ADC:
- AC — общая сторона;
- B = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и ADC равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы накрест лежащие при верхней и нижней сторонах и секущей диагонали, значит верхняя и нижняя стороны параллельны.
- ∠DAC = ∠BCA
Эти углы накрест лежащие при боковых сторонах и секущей диагонали. Поэтому боковые стороны четырёхугольника тоже параллельны. Значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные.
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащиз углов ∠1 = ∠2.
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все таки связано с параллельностью противоположных сторон.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Источник
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
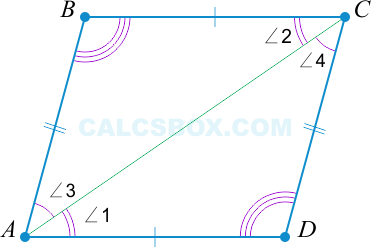
Первым делом проведем диагональ ( AC ). Получаются два треугольника: ( ABC ) и ( ADC ).
Так как ( ABCD ) — параллелограмм, то справедливо следующее:
( AD || BC Rightarrow angle 1 = angle 2 ) как лежащие накрест.
( AB || CD Rightarrow angle3 = angle 4 ) как лежащие накрест.
Следовательно, ( triangle ABC = triangle ADC ) (по второму признаку: ( angle 1 = angle 2, angle 3 = angle 4 ) и ( AC ) — общая).
И, значит, ( triangle ABC = triangle ADC ), то ( AB = CD ) и ( AD = BC ).
2. Противоположные углы тождественны
Согласно доказательству свойства 1 мы знаем, что ( angle 1 = angle 2, angle 3 = angle 4 ). Таким образом сумма противоположных углов равна: ( angle 1 + angle 3 = angle 2 + angle 4 ). Учитывая, что ( triangle ABC = triangle ADC ) получаем ( angle A = angle C ), ( angle B = angle D ).
3. Диагонали разделены пополам точкой пересечения
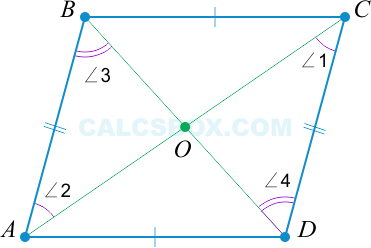
По свойству 1 мы знаем, что противоположные стороны тождественны: ( AB = CD ). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что ( triangle AOB = triangle COD ) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, ( BO = OD ) (напротив углов ( angle 2 ) и ( angle 1 )) и ( AO = OC ) (напротив углов ( angle 3 ) и ( angle 4 ) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
( AB = CD ); ( AB || CD Rightarrow ABCD ) — параллелограмм.
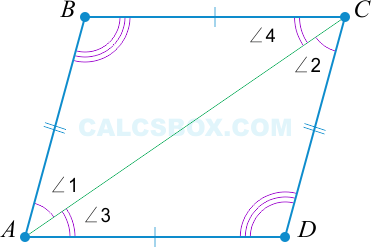
Рассмотрим подробнее. Почему ( AD || BC )?
( triangle ABC = triangle ADC ) по свойству 1: ( AB = CD ), ( angle 1 = angle 2 ) как накрест лежащие при параллельных ( AB ) и ( CD ) и секущей ( AC ).
Но если ( triangle ABC = triangle ADC ), то ( angle 3 = angle 4 ) (лежат напротив ( AD || BC ) (( angle 3 ) и ( angle 4 ) – накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
( AB = CD ), ( AD = BC Rightarrow ABCD ) — параллелограмм.
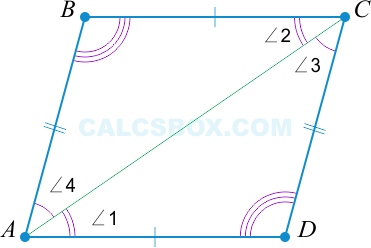
Рассмотрим данный признак. Еще раз проведем диагональ ( AC ).
По свойству 1 ( triangle ABC = triangle ACD ).
Из этого следует, что: ( angle 1 = angle 2 Rightarrow AD || BC ) и ( angle 3 = angle 4 Rightarrow AB || CD ), то есть ( ABCD ) — параллелограмм.
Второй признак верен.
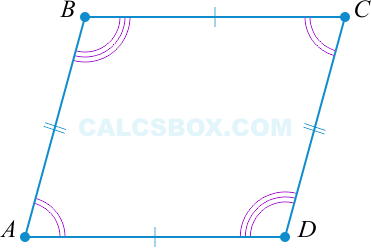
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
( angle A = angle C ), ( angle B = angle D Rightarrow ABCD ) — параллелограмм.
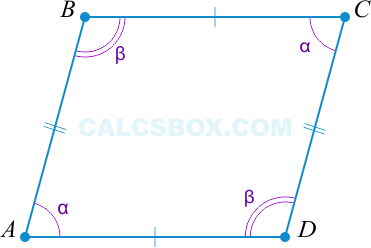
( 2 alpha + 2 beta = 360^{circ} ) (поскольку ( angle A = angle C ), ( angle B = angle D ) по условию).
Получается, ( alpha + beta = 180^{circ} ). Но ( alpha ) и ( beta ) являются внутренними односторонними при секущей ( AB ).
И то, что ( alpha + beta = 180^{circ} ) говорит и о том, что ( AD || BC ).
При этом ( alpha ) и ( beta ) — внутренние односторонние при секущей ( AB || CD ).
Третий признак верен.
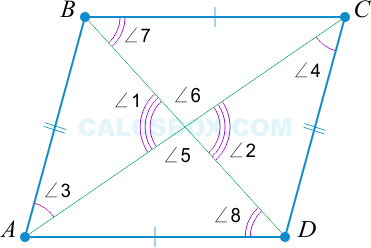
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
( AO = OC ); ( BO = OD Rightarrow ) параллелограмм.

( BO = OD ); ( AO = OC ), ( angle 1 = angle 2 ) как вертикальные ( Rightarrow triangle AOB = triangle COD ), ( Rightarrow angle 3 = angle 4 ), и ( Rightarrow AB || CD ).
Аналогично ( BO = OD ); ( AO = OC ), ( angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8 ), и ( Rightarrow AD || BC ).
Четвертый признак верен.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Источник
18 января 2021
- Определение
- Происхождение термина
- Свойства и признаки параллелограмма
- Как посчитать его периметр
- Как рассчитать площадь параллелограмма
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.
С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.
Определение параллелограмма
Итак,
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.
Выглядит эта фигура вот так:
Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.
Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.
Можно даже дать такие определения:
- Квадрат – это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник – это параллелограмм, у которого стороны пересекаются под прямым углом, но при этом они не равны между собой.
- Ромб – это параллелограмм, у которого все стороны равны между собой, но при этом они не пересекаются под прямым углом.
Происхождение термина «параллелограмм»
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.
Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».
Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.
Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.
Свойства и признаки параллелограмма
Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.
Возьмем в качестве примера еще раз нашу фигуру:
Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:
- Две противоположные стороны попарно параллельны.
- Две противоположные стороны попарно равны между собой.
- Две противоположные стороны и равны, и параллельны. В данном случае можно брать только одну пару сторон.
AD II BC и AD =BC. Или AB II CD и AB = CD
- Противоположные углы попарно равны между собой.
- Диагонали пересекаются в центре фигуры и делятся точкой пересечения на две равные части.
- Если сложить два соседних угла, то получится 180 градусов.
∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180
Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:
Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.
Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.
Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.
Как посчитать периметр параллелограмма
Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.
Снова возьмем для примера нашу фигуру:
Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:
Чтобы рассчитать периметр, надо просто сложить все стороны:
P = a + b + a + b
Но эту же формулу можно переиначить и по-другому:
P = 2a +2b
Или совсем просто:
P = (a + b) * 2
Это и есть формула периметра параллелограмма, которая записана во всех учебниках.
Как рассчитать площадь параллелограмма
С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.
- Вычисление площади параллелограмма по высоте.
Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.
- Вычисление площади параллелограмма по углам. Если известны длины сторон и хотя бы один угол, то можно применить следующую формулу.
- Вычисление площади параллелограмма по диагоналям. Для этого надо знать не только длину диагоналей, но и величину угла между ними. И тогда можно применять следующую формулу.
Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Комментарии и отзывы (1)
Сталкивалась с этим словом только в школе, на уроках геометрии, больше нигде ????
Источник
