Каким свойством обладает противолежащие стороны прямоугольника
Страница 98
Вопросы к параграфу
1. Какой четырёхугольник называют прямоугольником?
Прямоугольник – это четырёхугольник, у которого все углы прямые.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
Соседние стороны прямоугольника – это стороны, которые имеют общую вершину.
Противолежащие стороны прямоугольника – это стороны, которые не имеют общих вершин.
3. Что называют длиной и шириной прямоугольника?
Длиной прямоугольника называют длину более длинной пары его сторон, а шириной – длину более короткой пары сторон.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадрат – это прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
Фигуру называют симметричной, относительно прямой, если при сгибе по этой прямой противоположные части фигуры совпадают друг с другом.
7. Как называют прямую, относительно которой симметрична фигура?
Ось симметрии.
8. Какие вы знаете фигуры, имеющие ось симметрии?
Круг, равнобедренный и равносторонний треугольник, квадрат, прямоугольник.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
Прямоугольник, отличный от квадрата, имеет 2 оси симметрии.
Квадрат имеет 4 оси симметрии.
Равносторонний треугольник имеет 3 оси симметрии.
Решаем устно
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
Такой треугольник называют равносторонним. Его периметр равен P = 3a = 3 • 12 = 36 см.
Ответ: равносторонний, 36 см.
2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон – 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?
Задача может иметь 2 решения.
Решение 1.
Пусть 12 см – это длина основания равнобедренного треугольника. Тогда, при периметре 32 см, боковые стороны этого треугольника будут равны:
(32 – 12) : 2 = 20 : 2 = 10 (см) – длина каждой из боковых сторон треугольника.
Ответ: двумя другими сторонами будут две боковые стороны: 10 см и 10 см.
Решение 2:
Пусть 12 см – это длина одной из боковых сторон равнобедренного треугольника. Тогда вторая боковая сторона этого треугольника также равна 12 см, а основание, при периметре треугольника 32 см, будет равно:
32 – 12 • 2 = 32 – 24 = 8 (см) – длина основания треугольника.
Ответ: двумя другими сторонами будут: основание – 8 см и вторая боковая сторона – 12 см.
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
У равностороннего треугольника все три стороны равны, а периметр – это сумма все сторон треугольника.
Если одна сторона равностороннего треугольника меньше периметра на 10 см, значит сумма двух оставшихся сторон равна 10 см.
10 : 2 = 5 (см) – длина стороны равностороннего треугольника.
Ответ: 5 см.
4. Вычислите значение у по формуле у = х • х + 12, если:
1) х = 1
у = 1 • 1 + 12 = 1 + 12 = 13
Ответ: у = 13
2) х= 10
у = 10 • 10 + 12 = 100 + 12 = 112
Ответ: у = 112
Упражнения
359. Постройте:
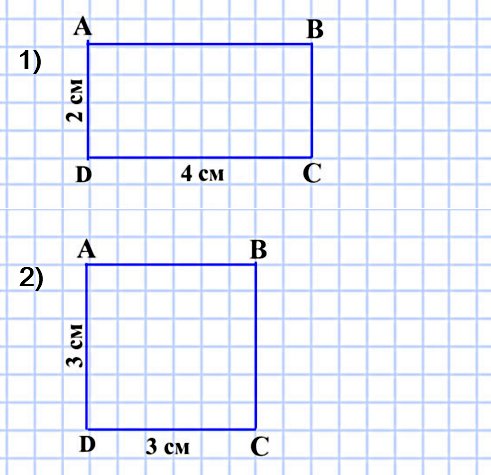
1) прямоугольник, соседние стороны которого равны 4 см и 2 см; 2) квадрат со стороной 3 см.
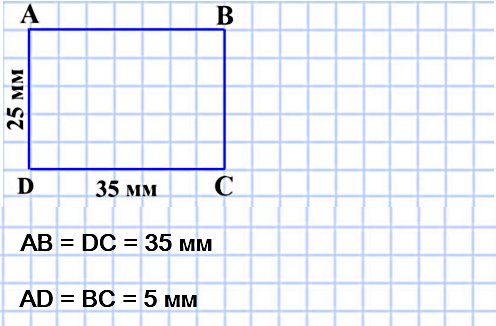
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.
Хотите сказать спасибо?
Подпишитесь на нашу группу вк!
Источник
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какой четырёхугольник называют прямоугольником?
Прямоугольник — это четырёхугольник, у которого все углы прямые.
2. Какие стороны прямоугольника называют соседними? Противолежащими?
- соседние стороны прямоугольника — это стороны, которые имеют общую вершину
- противолежащие стороны прямоугольника — это стороны, которые не имеют общих вершин
3. Что называют длиной и шириной прямоугольника?
Длиной и шириной прямоугольника называют соседние стороны прямоугольника.
4. Каким свойством обладают противолежащие стороны прямоугольника?
Противолежащие стороны прямоугольника равны.
5. Какую фигуру называют квадратом?
Квадрат — это прямоугольник, у которого все стороны равны.
6. Объясните, какие фигуры называют симметричными относительно прямой.
Фигуру называют симметричной, относительно прямой, если при сгибе по этой прямой противоположные части фигуры совпадают друг с другом.
7. Как называют прямую, относительно которой симметрична фигура?
Ось симметрии.
8. Какие вы знаете фигуры, имеющие ось симметрии?
Круг, равнобедренный и равносторонний треугольник, квадрат, прямоугольник.
9. Сколько осей симметрии имеет прямоугольник, отличный от квадрата? Квадрат? Равносторонний треугольник?
- Прямоугольник, отличный от квадрата, имеет 2 оси симметрии.
- Квадрат имеет 4 оси симметрии.
- Равносторонний треугольник имеет 3 оси симметрии.
Решаем устно
1. Каждая сторона треугольника равна 12 см. Как называют такой треугольник? Чему равен его периметр?
Такой треугольник называют равносторонним. Его периметр равен P = 3a = 3 • 12 = 36 см.
Ответ: равносторонний, 36 см.
2. Периметр равнобедренного треугольника равен 32 см, а одна из его сторон — 12 см. Найдите длины двух других сторон треугольника. Сколько решений имеет задача?
Задача может иметь 2 решения.
Решение 1.
Пусть 12 см — это длина основания равнобедренного треугольника. Тогда, при периметре 32 см, боковые стороны этого треугольника будут равны:
(32 — 12) : 2 = 20 : 2 = 10 (см) — длина каждой из боковых сторон треугольника.
Ответ: двумя другими сторонами будут две боковые стороны: 10 см и 10 см.
Решение 2:
Пусть 12 см — это длина одной из боковых сторон равнобедренного треугольника. Тогда вторая боковая сторона этого треугольника также равна 12 см, а основание, при периметре треугольника 32 см, будет равно:
32 — 12 • 2 = 32 — 24 = 8 (см) — длина основания треугольника.
Ответ: двумя другими сторонами будут: основание — 8 см и вторая боковая сторона — 12 см.
3. Найдите сторону равностороннего треугольника, если она меньше его периметра на 10 см.
У равностороннего треугольника все три стороны равны, а периметр — это сумма все сторон треугольника.
Если одна сторона равностороннего треугольника меньше периметра на 10 см, значит сумма двух оставшихся сторон равна 10 см.
10 : 2 = 5 (см) — длина стороны равностороннего треугольника.
Ответ: 5 см.
4. Вычислите значение у по формуле у = х • х + 12, если:
1) х = 1
у = 1 • 1 + 12 = 1 + 12 = 13
Ответ: у = 13
2) х= 10
у = 10 • 10 + 12 = 100 + 12 = 112
Ответ: у = 112
Упражнения
359. Постройте:
1) прямоугольник, соседние стороны которого равны 4 см и 2 см

AB = DC = 4 см
AD = BC = 2 см
2) квадрат со стороной 3 см

AB = BC = CD = DA = 3 см
360. Постройте прямоугольник, соседние стороны которого равны 25 мм и 35 мм.

AB = DC = 35 мм
AD = BC = 5 мм
361. Вычислите периметр:
1) прямоугольника, соседние стороны которого равны 42 см и 23 см
P = 2a + 2b = 2 • 42 + 2 • 23 = 84 + 46 = 130 (см)
Ответ: P = 130 см.
2) квадрата со стороной 8 дм
P = 4a = 4 • 8 = 32 (дм)
Ответ: P = 32 дм.
362. Найдите периметр прямоугольника, соседние стороны которого равны 13 мм и 17 мм.
P = 2a + 2b = 2 • 13 + 2 • 17 = 26 + 34 = 60 (мм)
60 мм = 6 см
Ответ: P = 6 см.
363. Какие из букв, изображённых на рисунке 135, имеют ось симметрии?

Ось симметрии имеют в данном случае буквы А, В, Е, Т.
364. Сколько осей симметрии имеет многоугольник, изображённый на рисунке 136?
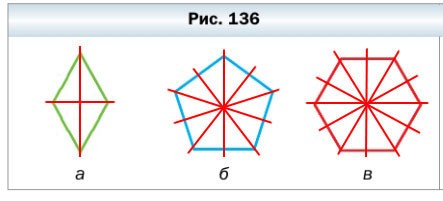
- а) робм — 2 оси симметрии
- б) правильный пятиугольник — 5 осей симметрии
- в) правильный шестиугольник — 6 осей симметрии
365. 1) Длина одной из сторон прямоугольника равна 14 см, что на 5 см больше длины соседней стороны. Найдите периметр прямоугольника.
1) 14 — 5 = 9 (см) — длина соседней стороны прямоугольника
P = 2a + 2b
2) 2 • 14 + 2 • 9 = 28 + 18 = 46 (см)
Ответ: P = 46 см.
2) Периметр прямоугольника равен 34 см, а одна из его сторон — 12 см. Найдите длину соседней стороны прямоугольника.
1) 12 • 2 = 24 (см) — сумма длин двух противоположных сторон прямоугольника
2) 34 — 24 = 10 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
3) 10 : 2 = 5 (см) — длина соседней стороны прямоугольника.
Ответ: 5 см.
366. Одна сторона прямоугольника равна 8 см, а соседняя — в 4 раза больше. Найдите периметр прямоугольника.
1) 8 • 4 = 32 (см) — длина соседней стороны прямоугольника.
P = 2a + 2b
2) 2 • 8 + 2 • 32 = 16 + 64 = 80 (см)
Ответ: P = 80 см.
367. Квадрат со стороной 12 см и прямоугольник, одна из сторон которого равна 8 см, имеют равные периметры. Найдите неизвестную сторону прямоугольника.
1) 12 • 4 = 48 (см) — периметр квадрата.
2) 8 • 2 = 16 (см) — сумма двух противоположных сторон прямоугольника.
3) 48 — 16 = 32 (см) — сумма длин двух других, соседних им, противоположных сторон треугольника.
4) 32 : 2 = 16 см (см) — длина соседней стороны прямоугольника.
Ответ: 16 см.
368. Прямоугольник, соседние стороны которого равны 42 см и 14 см, и квадрат имеют равные периметры. Найдите длину стороны квадрата.
1) 2 • 42 + 2 • 14 = 84 + 28 = 112 (см) — периметр прямоугольника.
2) 112 : 4 = 28 (см) — длина стороны квадрата.
Ответ: 28 см.
369. Сколько квадратов изображено на рисунке 137?
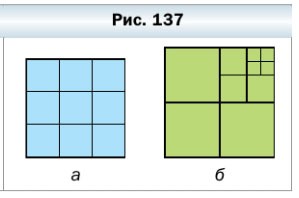
- а) На рисунке изображено 14 квадратов (9 маленьких + 4 средних + 1 большой).
- б) На рисунке изображено 13 квадратов (4 очень маленьких + 4 маленьких + 4 средних + 1 большой).
370. Из куска проволоки сделали модель пятиугольника (рис. 138).
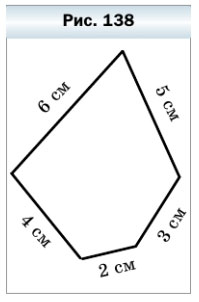
Какие из моделей перечисленных фигур, длины сторон которых выражаются натуральным числом сантиметров, можно сделать из этого куска проволоки: 1) квадрат; 2) пятиугольник, все стороны которого равны; 3) равносторонний треугольник?
1) 5 + 3 + 2 + 4 + 6 = 20 (см) — проволоки потребовалось для изготовления первоначальной модели.
2) 20 : 4 = 5 (см) — длина стороны квадрата, сделанного из этого куска проволоки.
3) 20 : 5 = 4 (см) — длина стороны пятиугольника, сделанного из этого куска проволоки.
4) 20 : 3 ≠ натуральному числу. Значит из этого куска проволоки нельзя изготовить равносторонний треугольник, длины сторон которого выражаются натуральным числом.
Ответ: квадрат и пятиугольник.
371. Прямоугольник ABCD разрезали на квадраты так, как показано на рисунке 139. Сторона наименьшего из квадратов равна 4 см. Найдите длины сторон прямоугольника ABCD.
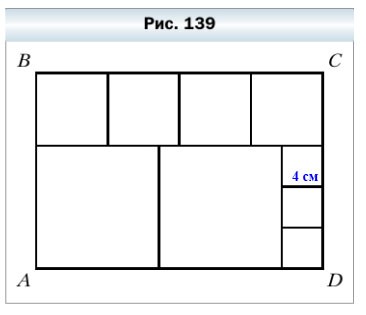
- На рисунки мы видим три вида квадратов: большие, средние и маленькие.
- По условию, сторона маленького квадрата равна 4 см. По рисунку видно, что сторона большого квадрата соответствует трём длинам сторон маленьких квадратов:
1) 4 • 3 = 12 (см) — длина стороны большого квадрата.
- Вдоль стороны AD прямоугольника ABCD расположено два больших квадрата и один маленький. Значит:
2) AD = 12 + 12 + 2 = 24 + 4 = 28 (см) — длина нижней стороны прямоугольника ABCD.
- У прямоугольника противоположные стороны равны. Значит:
3) AD = BC = 28 (см) — длина верхней стороны прямоугольника ABCD.
- Вдоль верхней стороны прямоугольника ABCD расположено 4 средних квадрата. Значит:
4) 28 : 4 = 7 (см) — длина стороны среднего квадрата.
- Вдоль боковой стороны AB прямоугольника ABCD расположен один большой квадрат и один средний квадрат. Значит:
5) AB = 12 + 7 = 19 (см) — длина боковой стороны прямоугольника ABCD
- У прямоугольника противоположные стороны равны. Значит:
6) AB = CD = 19 (см) — длина противоположной боковой стороны прямоугольника ABCD
Ответ: у прямоугольника ABCD две стороны по 19 см и дву стороны по 28 см.
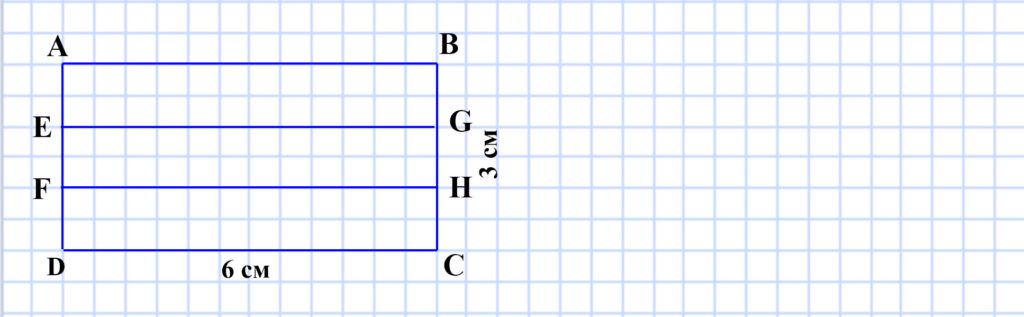
372. Начертите прямоугольник, соседние стороны которого равны 3 см и 6 см. Разделите его на три равных прямоугольника. Вычислите периметр каждого из полученных прямоугольников. Сколько решений имеет задача?
Задача имеет 2 решения.
Решение 1.

ABGE = EGHF = FHCD
a = AB = EG = FH = DC = 6 (см) — длина стороны малого прямоугольника.
b = AE = EF = FD = BG = GH = HC = 3 : 3 = 1 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 6 + 2 • 1 = 12 + 2 = 14 (см) — периметр малого прямоугольника.
Ответ: P = 14 см.
Решение 2.

AKMD = KLNM = LBCN
a = AD = KM = LN = BC = 3 (см) — длина стороны малого прямоугольника.
b = AK = KL = LB = DM = MN = NC = 6 : 3 = 2 (см) — длина соседней стороны малого прямоугольника.
P = 2a + 2b = 2 • 3 + 2 • 2 = 6 + 4 = 10 (см) — периметр малого прямоугольника.
Ответ: P = 10 см.
373. Существует ли среди прямоугольников с периметром 12 см такой, который можно разделить на два равных квадрата? В случае положительного ответа выполните рисунок и вычислите периметр каждого из полученных квадратов.

Да, такой прямоугольник существует. Например, прямоугольник ABCD со сторонами AB = DC= 4 см и AD = BC = 2 см. Его периметр P = 12 см (2 • 4 + 2 • 2 = 8 + 4 = 12) и его можно разделить на 2 равных квадрата со сторонами 2 см. Это квадраты AMLD и MBCL.
Вычислим периметр полученных квадратов (так как квадраты равные, то и их периметры тоже равны):
P = 4а = 4 • 2 = 8 (см).
Ответ: Да, возможно. Периметр каждого из образованных квадратов AMLD и MBCL равен 8 см.
374. Как надо разрезать квадрат на четыре равные части, чтобы из них можно было сложить два квадрата?

375. Как надо разрезать равнобедренный прямоугольный треугольник на четыре равные части, чтобы из них можно было сложить квадрат?

376. Как надо разрезать прямоугольник со сторонами 8 см и 4 см на четыре части, чтобы из них можно было сложить квадрат?

377. Как надо разрезать квадрат на треугольник и четырёхугольник, чтобы из них можно было сложить треугольник?

378. Как надо разрезать квадрат со стороной 6 см на две части по ломаной, состоящей из трёх звеньев, чтобы из полученных частей можно было сложить прямоугольник?

Упражнения для повторения
379. Проведите прямую МК, луч PS и отрезок АВ так, чтобы луч PS пересекал отрезок АВ и прямую МК, а прямая МК не пересекала отрезок АВ.

380. В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
- Предположим, что в магазине продали 55 кг лимонов 36 кг апельсинов и 34 кг мандаринов. Тогда можно найти массу фруктов оставшихся в магазине:
1) 740 — (55 + 36 + 34) = 740 — (55 + 70) = 740 — 125 = 615 (кг) — фруктов осталось в магазине после продажи.
- По условию задачи в магазине остались равные массы лимонов, апельсинов и мандарины. Узнаем сколько килограммов каждого вида фруктов осталось:
2) 615 : 3 = 205 (кг) — масса каждого вида фруктов осталось в магазине.
- Теперь найдём какова масса фруктов изначально:
3) 205 + 55 = 260 (кг) — лимонов было в магазине изначально.
4) 205 + 36 = 241 (кг) — апельсинов было в магазине изначально.
5) 205 + 34 = 239 (кг) — мандаринов было в магазине изначально.
Ответ: лимонов — 260 кг, апельсинов — 241 кг, мандаринов — 239 кг.
381. От дома до дачи можно доехать на автобусе, или на электропоезде, или на маршрутном такси. В таблице указано время, которое надо затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Каким видом транспорта при этом надо воспользоваться?
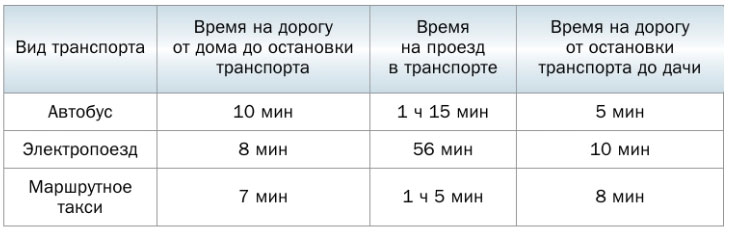
1) 10 мин + 1 ч 15 мин + 5 мин = 1 ч 30 мин — потребуется для поездки на автобусе.
2) 8 мин + 56 мин + 10 мин = 74 мин = 1 ч 14 мин — потребуется для поездки на электропоезде.
3) 7 мин + 1 ч 5 мин + 8 мин = 1 ч 20 мин — потребуется для поездки на маршрутном такси.
Ответ: наименьшее время на дорогу — 1 ч 14 мин, для этого надо воспользоваться электропоездом.
382. Найдите сумму корней уравнений:

Задача от мудрой совы
383. Как с помощью пятилитрового бидона и трёхлитровой банки набрать на берегу реки 4 л воды?
- Наливаем из реки полный 5-литровый бидон.
- Переливаем 3 литра в 3-х литровую банку. В 5-ти литровом бидоне останется 2 литра воды.
- Выливаем из 3-х литровой банки воду обратно в реку.
- Переливаем остаток воды из 5-литрового бидона (2 литра) в 3-литровую банку.
- Наливаем из реки полный 5-литровый бидон.
- Переливаем воду из 5-литрового бидона в 3-литровую банку.
При последнем действии мы сможем вылить в банку только 1 литр воды, так как в ней уже есть 2 литра воды. То есть в 5-литровом бидоне останется искомые 4 литра воды (5 — 1 = 4).
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Источник
Этап урока. Методы и приемы
Хроно-метраж
Содержание урока.
Деятельность
учителя
Деятельность ученика
Планируемые результаты (УУД)
Орг.момент
Словесный метод: ответы на вопросы.
Мотивационный
Словесн.: восприятие новой информации.
Актуализация опорных знаний
Постановка учебной цели и задач
Решение частных звдач
Физминутка
Первичное закрепление
Рефлексия
Словест.ответы на вопросы, самоанализ
1мин
5мин
5мин
35мин
2мин
2мин
Здравствуйте, ребята! Садитесь! Сегодня, друзья мы отправимся в путь
Хорошее настроение взять с собой не позабудь!
Ждут нас встречи и друзья,
Четырёхугольников семья.
Дети, улыбнитесь друг другу, пожелайте удачи, ведь удача нам сегодня очень пригодится! Вы постарайтесь производить все расчеты точно, работать быстро и, самое главное, дружно!
Сейчас открываем тетради и записываем сегодняшнее число и классная работа. На доске можете посмотреть образец. (19 февраля. Классная работа). Пишите красиво и правильно. Кто готов, покажите мне.
И начнем мы с минутки чистописания. Послушайте загадку и скажите мне, какую цифру мы должны прописать.
Сколько лет в яйце цыпленку,
Сколько крыльев у котенка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра… (ноль)Сколько солнышек за тучкой,
Сколько стержней в авторучке,
Сколько у слона носов,
Сколько на руке часов?
Сколько ног у мухомора
И попыток у сапера,
Знает и собой гордится,
Цифра-столбик… (единица)
Молодцы! Прописываем целую строчку цифру 0 (1). Не забудьте отметить самую красивую.
Сегодня мы продолжим открывать тайны математики и отправимся в удивительную страну ГЕОМЕТРИЯ и встретимся с жителями, которые в ней живут.
Слайд 1
– По координатам букв прочитайте слово.
Слайды 2-3
-А кто знает, что означает это слово геометрия.
Давайте посмотрим в словаре Ожегова.
Слайд 4
– А какие геометрические фигуры мы знаем?
– Какие свойства этих геометрических фигур вы знаете?
– Назовите предметы или части предметов, которые имеют такую геометрическую форму.
– Для чего нам нужно знать свойства геометрических фигур?
Слайд 5
– Найдите среди них фигуры с одинаковыми свойствами.
– Докажите, что эти фигуры прямоугольники.
– Как проверить? (Все углы прямоугольника прямые)
Используя модели прямого угла, найдите среди данных фигур прямоугольник.
– Какое свойство прямоугольника мы использовали для того, чтобы найти прямоугольник?
Слайд 6
– А какие свойства есть еще у прямоугольника? Какую же мы поставим перед собой цель? (Выяснить, какими свойствами обладает прямоугольник)
Итак, тема урок, «Свойства прямоугольника»
Слайд 7
Посмотрите внимательно на прямоугольник, вглядитесь, может, вы еще что-то интересное заметите у прямоугольника?
Дополнительно: Обратите внимание на стороны прямоугольника. ( Стороны, находящиеся друг напротив друга – одинаковые.)
– А как можно назвать эти стороны, которые находятся напротив друг друга. (Эти стороны, находящиеся напротив друг друга, называются противоположными.)
Почему они так называются? (Положены (лежат) друг против друга.)
А что это значит: стороны, находящиеся друг напротив друга одинаковые? (Они равны по длине.)8 слайд
Найдем их и покажем синим и красным цветом противоположные стороны.
– А как проверить наше наблюдение, что противоположные стороны прямоугольника равны? (Измерить длину противоположных сторон с помощью линейки, сравнивать сгибанием. Противоположные стороны прямоугольника равны)
Слайд 9
Проанализируйте нашу работу и сделайте вывод.
Сравнить с выводом учебника на стр. 32
Показ ритмических движений.
Раз, два, три, четыре, пять,
Надо нам присесть и встать.
Руки вытянуть пошире.
Раз, два, три, четыре, пять,
Наклониться – три, четыре,
И на месте поскакать.
На носки, затем на пятки.
Лень отбросить и опять.
Сесть за парту, взять тетрадку,
И работу продолжать.
Работа с заданием №1 в учебнике на странице 32.
Задание №1, Кто прочитает?
Что изменилось? (углы)
Задание №2
А теперь задание 2. Кто прочитает задачу?
О ком или о чем говорится в данной задаче?(о тележке, о подъёмном кране, о деталях конструктора) Что нам известно? (чтобы сделать тележку нужно 12 деталей, чтобы сделать подъемный кран , нужно 20 деталей) А что там нужно найти?( тут нет вопроса, его нужно придумать)
Какой вопрос мы можем с вами придумать? ( Сколько всего деталей нужно Никите, чтобы построить тележку и подъёмный кран?)
Значит, как будет выглядеть краткая запись, какие главные слова мы будем использовать? Выходи к доске и запиши, а остальные в тетради
тележка – 12д..
подъемный кран -20д..}?д..
Прочитайте мне вопрос. А мы сможем ответить на этот вопрос? (да) Каким действием будем находить?( сложением) Каким выражением запишем?.
12+20=32 (д.) понадобится Никите.
Мы можем сказать, что решили данную задачу? Верно, мы ответили на вопрос, значит, решили задачу. Что нужно записать в конце? Ответ, верно. Записываем ответ.
Ответ:32 детали.
Какой еще вопрос подойдет к данному условию?
( Мы можем узнать на слолько больше деталей нужно для подъёмного крана или на сколько меньше деталей нужно для тележки?)
Каким действием будем находить?( вычитанием) Каким выражением запишем?.
20-12=8 (д.) на 8деталей больше понадобится Никите, чтобы построить кран.
Мы можем сказать, что решили данную задачу? Верно, мы ответили на вопрос, значит, решили задачу. Что нужно записать в конце? Ответ, верно. Записываем ответ.
Ответ: на 8 деталей больше.
Задание №4 (3 человека у доски)
42-27=
54-36=
92-53=
64+28=
87+13=
72+19=
Ребята, вы сегодня очень активно работали! Наш урок подходит к завершению. Давайте с вами подведем итоги. Что нового вы сегодня узнали? Какой вывод вы сделали сами? А вы научились применять его. Молодцы, я за вас рада!
А теперь возьмите в руки ваши карандаши: зеленый, желтый и красный. Поднимите ЗЕЛЕНЫЙ карандаш, если – вы довольны собой, вам понравился урок, у вас все получилось, во время урока не возникало трудностей. ЖЕЛТЫЙ, если – у вас не все получилось, что-то было непонятно, но вы постараетесь на следующем занятии.
И КРАСНЫЙ – вам ничего не понятно и сегодняшний урок не понравился.
Молодцы! Спасибо вам за урок! До свидания!
Приветствуют учителя.
Слушают учителя
Разгадывают загадки
Пишут чисто и аккуратно
Р
ешают самостоятельо.
заполнение карточек.
Повторение ритмических движений.
проводят само- и
взаимоконтроль
Выполняют задание; анализируют;
делают выводы; слушают учителя; проводят само- и взаимоконтроль.
Проводят рефлексию.
Делают вывод.
Отвечают на вопросы.
Положительное отношение к урокам математики, формирование ценностных ориентаций.
Л:самоопределение и смыслообразование.
П: применять базовые знания для решения конкретной проблемы.
К: высказывать свое мнение при обсуждении задания.
Умение выбирать и использовать в ходе решения изученные свойства арифметических действий.
Р: контроль и самоконтроль учебных действий.
П: применять базовые знания для решения конкретной проблемы.
К: высказывать свое мнение при обсуждении задания.
Умение выбирать и использовать в ходе решения изученные свойства арифметических действий.
Р: контроль и самоконтроль учебных действий.
К: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
аргументация своего мнения и позиции.
П: применять базовые знания для решения конкретной проблемы.
П: Владеть общими приемами решения задач.
Строить логическую цепь рассуждений.
Р: отслеживать цель учебной деятельности
Л: способность к самооценке на основе критерия успешности учебной деятельности.
Источник
