Каким свойством обладает радиус проведенный в точку касания прямой и окружности

- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Касательная к окружности
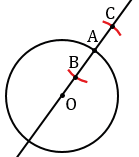
Касательная к окружности – прямая, имеющая с окружностью одну общую точку, которая называется точкой касания прямой и окружности. На рисунке 1 прямая  – касательная к окружности, точка Н – точка касания прямой
– касательная к окружности, точка Н – точка касания прямой  и окружности с центром в точке О.
и окружности с центром в точке О.
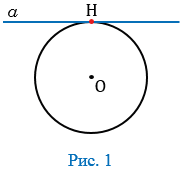
Свойство касательной к окружности
Теорема
Доказательство
Дано:  – касательная к окружности с центром в точке О, Н – точка касания (Рис. 2).
– касательная к окружности с центром в точке О, Н – точка касания (Рис. 2).
Доказать: ОН
 .
.
Доказательство:
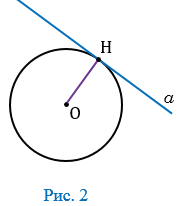
Предположим, что ОН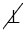
 . Тогда радиус ОН является наклонной к прямой
. Тогда радиус ОН является наклонной к прямой  . При этом перпендикуляр, проведенный из точки О к прямой
. При этом перпендикуляр, проведенный из точки О к прямой  , меньше наклонной ОН, тогда расстояние от центра О окружности до прямой
, меньше наклонной ОН, тогда расстояние от центра О окружности до прямой  меньше радиуса. Следовательно прямая
меньше радиуса. Следовательно прямая  и окружность будут иметь две общие точки, что противоречит условию: прямая
и окружность будут иметь две общие точки, что противоречит условию: прямая  – касательная. Поэтому наше предположение неверно, значит, ОН
– касательная. Поэтому наше предположение неверно, значит, ОН 
 . Теорема доказана.
. Теорема доказана.
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство
Дано: АВ и АС – касательные к окружности с центром в точке О, В и С – точки касания (Рис. 3).
Доказать: АВ = АС и  3 =
3 = 4.
4.
Доказательство:
 1 =
1 = 2 = 900, т.к. ОВ
2 = 900, т.к. ОВ АВ, ОС
АВ, ОС АС по теореме о свойстве касательной (смотри выше), поэтому
АС по теореме о свойстве касательной (смотри выше), поэтому 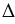 АВО и
АВО и 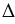 АСО прямоугольные. При этом ОВ = ОС (радиусы), АО – общая, следовательно,
АСО прямоугольные. При этом ОВ = ОС (радиусы), АО – общая, следовательно, 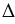 АВО =
АВО =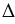 АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и
АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и  3 =
3 = 4. Что и требовалось доказать.
4. Что и требовалось доказать.
Теорема, обратная теореме о свойстве касательной (признак касательной)
Теорема
Доказательство
Дано: ОН – радиус окружности с центром в точке О, Н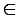
 , ОН
, ОН
 (Рис. 4).
(Рис. 4).
Доказать:  – касательная.
– касательная.
Доказательство:
По условию радиус ОН 
 , поэтому расстояние от центра окружности до прямой
, поэтому расстояние от центра окружности до прямой  равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.
равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.
Задача
Через данную точку А окружности с центром О провести касательную к этой окружности.
Дано: точка А лежит на окружности с центром в точке О.
Провести касательную  к окружности так, что А
к окружности так, что А
 .
.
Решение:
Строим с помощью циркуля окружность с центром в точкеО, отмечаем на данной окружности точку А.
Далее проводим прямую ОА и строим прямую  , проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.
, проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.
Затем строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекаются в двух точках, обозначим их Р и Q. Через точки Р и Q с помощью линейки проводим прямую  , которая будет перпендикулярна к прямой ОА.
, которая будет перпендикулярна к прямой ОА.
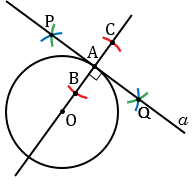
Итак, 
 ОА, ОА – радиус, следовательно,
ОА, ОА – радиус, следовательно,  – искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).
– искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Взаимное расположение прямой и окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 634,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 639,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 643,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 644,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 673,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 677,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 23,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 736,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1171,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
§ 20. Некоторые свойства окружности. Касательная к окружности

Теорема 20.1
Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Рис. 287 |
|
Доказательство
Если хорда является диаметром, то теорема очевидна.
На рисунке 287 изображена окружность с центром O, M — точка пересечения диаметра CD и хорды AB, CD ⊥ AB. Надо доказать, что AM = MB.
Проведём радиусы OA и OB. В равнобедренном треугольнике AOB (OA = OB) отрезок OM — высота, а значит, и медиана, т. е. AM = MB. 

Теорема 20.2
Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.
На рисунке 288 показаны все возможные случаи взаимного расположения прямой и окружности. На рисунке 288, а они не имеют общих точек, на рисунке 288, б — имеют две общие точки, на рисунке 288, в — одну.

Определение
Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 288, в прямая a — касательная к кругу с центром в точке O, A — точка касания.
Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 289 изображён отрезок AB, который касается окружности в точке С.

Теорема 20.3
(свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Доказательство
На рисунке 290 изображена окружность с центром O, A — точка касания прямой a и окружности. Надо доказать, что OA ⊥ a.
Рис. 289 | Рис. 290 | Рис. 291 |
|
|
|
Предположим, что это не так, т. е. отрезок OA — наклонная к прямой a. Тогда из точки O опустим перпендикуляр OM на прямую a (рис. 291). Поскольку точка A — единственная общая точка прямой a и круга с центром O, то точка M не принадлежит этому кругу. Отсюда OM = MB + OB, где точка B — точка пересечения окружности и перпендикуляра OM. Отрезки OA и OB равны как радиусы окружности. Таким образом, OM > OA. Получили противоречие: перпендикуляр OM больше наклонной OA. Следовательно, OA ⊥ a. 

Теорема 20.4
(признак касательной к окружности)
Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.
Доказательство
Рис. 292 |
|
На рисунке 290 изображена окружность с центром в точке O, отрезок OA — её радиус, точка A принадлежит прямой a, OA ⊥ a. Докажем, что прямая a — касательная к окружности.
Пусть прямая a не является касательной, а имеет ещё одну общую точку B с окружностью (рис. 292). Тогда ∆AOB — равнобедренный (OA = OB как радиусы). Отсюда ∠OBA = ∠OAB = 90°. Получаем противоречие: в треугольнике AOB есть два прямых угла. Следовательно, прямая a является касательной к окружности. 

Следствие
Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
Рис. 293 |
|
Докажите это следствие самостоятельно.

Задача. Докажите, что если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.
Решение. На рисунке 293 изображена окружность с центром O. Прямые AB и AC — касательные, точки B и C — точки касания. Надо доказать, что AB = AC.
Проведём радиусы OB и OC в точки касания. По свойству касательной OB ⊥ AB и OC ⊥ AC. В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC. 

- Как делит хорду диаметр, перпендикулярный ей?
- Чему равен угол между хордой, отличной от диаметра, и диаметром, делящим эту хорду пополам?
- Опишите все возможные случаи взаимного расположения прямой и окружности.
- Какую прямую называют касательной к окружности?
- Каким свойством обладает радиус, проведённый в точку касания прямой и окружности?
- Сформулируйте признак касательной к окружности.
- Каким свойством обладают касательные, проведённые к окружности через одну точку?

Практические задания

507.Начертите окружность с центром O, проведите хорду AB. Пользуясь угольником, разделите эту хорду пополам.
508.Начертите окружность с центром O, проведите хорду CD. Пользуясь линейкой со шкалой, проведите диаметр, перпендикулярный хорде CD.
509.Начертите окружность, отметьте на ней точки A и B. Пользуясь линейкой и угольником, проведите прямые, которые касаются окружности в точках A и B.
510.Проведите прямую a и отметьте на ней точку M. Пользуясь угольником, линейкой и циркулем, проведите окружность радиуса 3 см, которая касается прямой a в точке M. Сколько таких окружностей можно провести?

Упражнения

511.На рисунке 294 точка O — центр окружности, диаметр CD перпендикулярен хорде AB. Докажите, что ∠AOD = ∠BOD.
512.Докажите, что равные хорды окружности равноудалены от её центра.
513.Докажите, что если хорды окружности равноудалены от её центра, то они равны.
514.Верно ли, что прямая, перпендикулярная радиусу окружности, касается этой окружности?
515.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠BAD = 35° (рис. 295). Найдите ∠AOB.
516.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠AOB = 80° (см. рис. 295). Найдите ∠BAC.
517.Дана окружность, диаметр которой равен 6 см. Прямая a удалена от её центра на: 1) 2 см; 2) 3 см; 3) 6 см. В каком случае прямая a является касательной к окружности?
518.В треугольнике ABC известно, что ∠C = 90°. Докажите, что:
1)прямая BC является касательной к окружности с центром A, проходящей через точку C;
2)прямая AB не является касательной к окружности с центром C, проходящей через точку A.

519.Докажите, что диаметр окружности больше любой хорды, отличной от диаметра.
520.В окружности с центром O через середину радиуса провели хорду AB, перпендикулярную ему. Докажите, что ∠AOB = 120°.
521.Найдите угол между радиусами OA и OB окружности, если расстояние от центра O окружности до хорды AB в 2 раза меньше: 1) длины хорды AB; 2) радиуса окружности.
522.В окружности провели диаметр AB и хорды AC и CD так, что AC = 12 см, ∠BAC = 30°, AB ⊥ CD. Найдите длину хорды CD.
523.Через точку M к окружности с центром O провели касательные MA и MB, A и B — точки касания, ∠OAB = 20°. Найдите ∠AMB.
524.Через концы хорды AB, равной радиусу окружности, провели две касательные, пересекающиеся в точке C. Найдите ∠ACB.
525.Через точку C окружности с центром O провели касательную к этой окружности, AB — диаметр окружности. Из точки A на касательную опущен перпендикуляр AD. Докажите, что луч AC — биссектриса угла BAD.
526.Прямая AC касается окружности с центром O в точке A (рис. 296). Докажите, что угол BAC в 2 раза меньше угла AOB.
Рис. 294 | Рис. 295 | Рис. 296 |
|
|
|
527.Отрезки AB и BC — соответственно хорда и диаметр окружности, ∠ABC = 30°. Через точку A провели касательную к окружности, пересекающую прямую BC в точке D. Докажите, что ∆ABD — равнобедренный.
528.Известно, что диаметр AB делит хорду CD пополам, но не перпендикулярен ей. Докажите, что CD — также диаметр.

529.Найдите геометрическое место центров окружностей, которые касаются данной прямой в данной точке.
530.Найдите геометрическое место центров окружностей, которые касаются обеих сторон данного угла.
531.Найдите геометрическое место центров окружностей, которые касаются данной прямой.
532.Прямые, касающиеся окружности с центром O в точках A и B, пересекаются в точке K, ∠AKB = 120°. Докажите, что AK + BK = OK.
533.Окружность касается стороны AB треугольника ABC в точке M и касается продолжения двух других сторон. Докажите, что сумма длин отрезков BC и BM равна половине периметра треугольника ABC.
Рис. 297 |
|
534.Через точку C проведены касательные AC и BC к окружности, A и B — точки касания (рис. 297). На окружности взяли произвольную точку M, лежащую в одной полуплоскости с точкой C относительно прямой AB, и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметр треугольника DEC не зависит от выбора точки M.

Упражнения для повторения
535.Докажите, что середина M отрезка, концы которого принадлежат двум параллельным прямым, является серединой любого отрезка, который проходит через точку M и концы которого принадлежат этим прямым.
536.Отрезки AB и CD лежат на одной прямой и имеют общую середину. Точку M выбрали так, что треугольник AMB — равнобедренный с основанием AB. Докажите, что ∆CMD также является равнобедренным с основанием CD.
537.На стороне MK треугольника MPK отметили точки E и F так, что точка E лежит между точками M и F, ME = EP, PF = FK. Найдите угол M, если ∠EPF = 92°, ∠K = 26°.
538.В остроугольном треугольнике ABC проведена биссектриса BM, из точки M на сторону BC опущен перпендикуляр MK, ∠ABM = ∠KMC. Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте
539.Установите закономерность форм фигур, изображённых на рисунке 298. Какую фигуру надо поставить следующей?
Рис. 298 |
|
Источник
- Главная
- Вопросы & Ответы
- Вопрос 16362988
более месяца назад
Просмотров : 1
Ответов :
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Укажите достижение прикладного искусство казахского народа
более месяца назад
Смотреть ответ
Просмотров :
Ответов : 1
Почему началось появление Средневековых городов
более месяца назад
Смотреть ответ
Просмотров :
Ответов : 1
помогите с английским СРОЧНО
более месяца назад
Смотреть ответ
Просмотров :
Ответов : 1
Картинок: 1
НОМЕР 117 38м-19м=? НОМЕР 118 Протяженность озера Сарапууярв примерно 310м, а протяженность озера Киккаярв примерно в 3раза больше. На сколько метров протяженность озера Киккаярв больше, чем озера Сарапууярв? ПОМОГИТЕ ПОЖАЛУЙСТА. НУЖНО ДО ЗАВТРА!!!
более месяца назад
Смотреть ответ
Просмотров : 1
Ответов :
Мое любимое животное по английскому 6 предложений
более месяца назад
Смотреть ответ
Просмотров : 1
Ответов : 1
Источник











