Каким свойством обладает равнобедренный треугольник
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
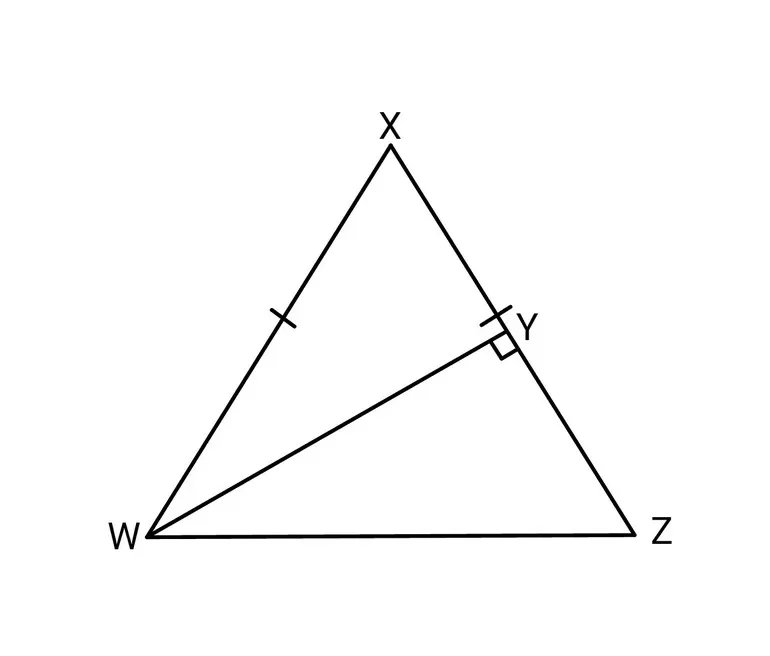
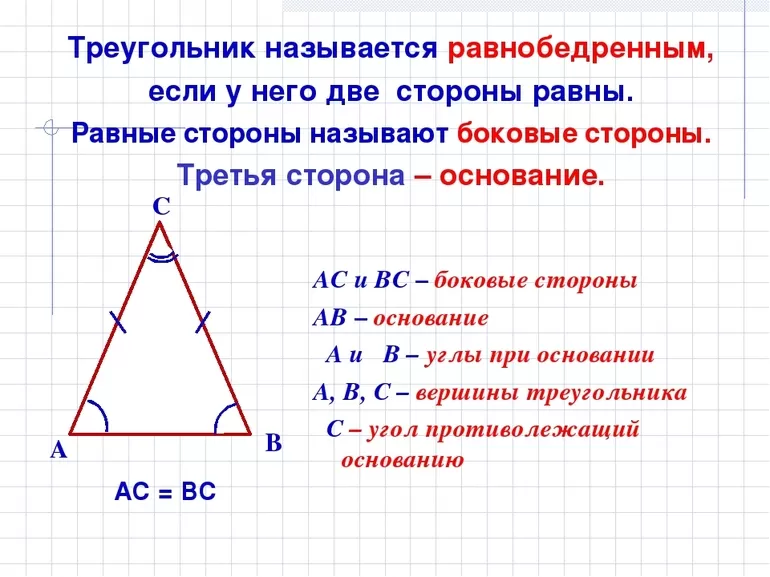
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Источник
Определение равнобедренного треугольника
Определение равнобедренного треугольника звучит проще простого:
Равнобедренным называется треугольник, у которого две стороны равны.
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
Геометрия в 7 классе полна острых углов. Чтобы ваш ребенок миновал их круглым отличником, запишите его на бесплатный пробный урок математики в онлайн-школу Skysmart.
Наши опытные преподаватели научат с закрытыми глазами отличать равнобедренный треугольник от равностороннего, а интерактивная платформа не даст заскучать на уроках.
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
- Δ ABC
- Высота BH делит Δ ABC на два прямоугольных треугольника ABH и CBH
- Δ ABH = Δ CBH, поскольку гипотенузы и катет равны по теореме Пифагора
- Согласно теореме 1: в треугольниках ABH и BCH ∠ BАH = ∠ BСH, поскольку углы при основании равнобедренного треугольника равны
- Так как Δ ABC — равнобедренный, то его боковые стороны равны AB = BC
- AH = CH, поскольку точка H делит основание Δ ABC на две равные части
- Δ ABH = Δ BCH
- Значит, отрезок BH одновременно биссектриса, медиана и высота равнобедренного треугольника ABC
Вуаля, сразу три теоремы доказаны.
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Доказательство:
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, то такой треугольник снова равнобедренный!
- Если два угла треугольника равны, такой треугольник является равнобедренным.
- В равнобедренном треугольнике углы при основании равны.
- Углы при основании в равнобедренном треугольнике — всегда острые.
- Сумма углов равнобедренного треугольника равна 180 градусам.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘
Еще больше тренировок — в детской школе Skysmart. Записывайте ребенка на бесплатный урок математики и приходите сами: покажем, как все устроено и наметим индивидуальную программу занятий.
Источник

Общие сведения
Замкнутую фигуру, состоящую из трёх пересекающихся прямых и такого же количества внутренних углов, называют треугольником. Отрезки, которые соединяют точки, образующие фигуру, называют сторонами. Для обозначения используют малые латинские буквы. Точка, в которой соединяется 2 стороны, называется вершиной. Её принято подписывать заглавными буквами, например, A, B, C.
Существует несколько видов фигур по типу углов и по длинам сторон:
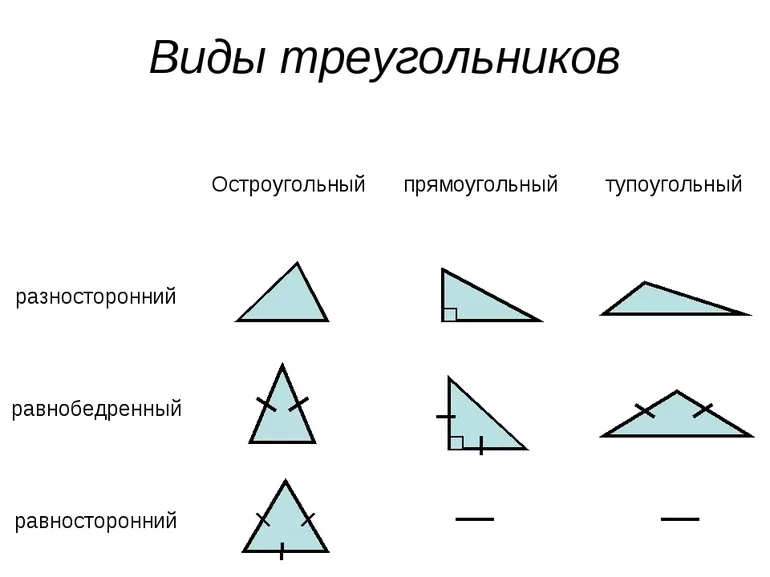
- разносторонние — все отрезки, образующие многоугольник, имеют различную длину;
- равнобедренные — 2 стороны одинаковы;
- равносторонние — все 3 стороны равны;
- остроугольными — 3 угла многоугольника являются острыми;
- прямоугольными — 2 стороны образуют угол в 90 градусов;
- тупоугольными — размер одного угла превышает 90 градусов.
Отличительная черта фигуры — сумма углов равняется 180 градусов. Это один из самых важных признаков, позволяющих отнести многоугольник к треугольникам. Причём каждая такая фигура имеет замечательные линии и точки.
Прежде всего это медиана — отрезок, построенный из вершины к центру противолежащей стороны, разделяющий фигуру на 2 равных треугольника. Биссектрисой называют линию, построенную к противоположной стороне и разделяющую угол на 2 равные части. Также можно опустить перпендикуляр на любую сторону из вершины. Называют такую линию высотой.
В треугольнике можно провести по 3 любых таких линии. Причём точка пересечения отрезков имеет своё название: 3 высоты встречаются в ортоцентре, а биссектрисы — инцентре. Если в треугольник вписать окружность, её центр совпадёт с местом пересечения медиан. Эта точка является центроидом, центром массы фигуры. Кроме этого, можно описать круг, в центре которого будут пересекаться серединные перпендикуляры.
Признаки равнобедренной фигуры
Существует 4 явления, с помощью которых можно определить принадлежность тела к треугольникам. Все они сгруппированы в 3 теоремы:
- Если в треугольнике построить медиану, при этом она будет совпадать с высотой, он является равнобедренным. Аналогично можно утверждать о принадлежности фигуры к равнобедренному типу, когда биссектриса совпадает с высотой.
- Если 2 угла равны, треугольник равнобедренный.
- Если медиана и биссектриса совпадают, причём построены из одного угла, фигура называется равнобедренной.
Для доказательства первой теоремы нужно использовать признаки равенства треугольников. Если изобразить на чертеже фигуру ABC и из вершины B построить высоту, согласно заданным данным, она будет медианой или биссектрисой. В первом случае противоположная сторона будет разделена на 2 равные части AD и DC. Значит, треугольники ABD и DBC одинаковые. Отсюда следует, что у фигур есть равные стороны: AB = BC., то есть боковые грани имеют одинаковую длину, что и требуется по определению.
В случае с биссектрисой ход рассуждений будет такой же. Отличие заключается лишь в том, что используется второй признак равенства: если грань и 2 прилежащих к ней угла одного треугольника совпадают со стороной и двумя прилежащими к ней углам другого, они равны.
Доказательство второй теоремы следует построить на нахождении равных сторон. Для этого нужно отложить серединный перпендикуляр a и доказать, что линия будет проходить через вершину B. Если она не будет пересекать угол B, она касается AB или BC. Пусть точкой пересечения перпендикуляра будет M. Тогда по первому признаку AKM = CKM, значит, углы MCK и MAK также равны. По условию теоремы MCK = MAB → MAK = MAB, что противоречит аксиоме измерения углов. Отсюда можно утверждать, что серединный перпендикуляр не пересекает BC или AC. Значит, прямая проходит через вершину B.
Третью теорему легко можно доказать, отложив на луче BM равный ему по длине отрезок. Затем, соединив A и D, построить треугольник ADM. Углы ABM и ADM одинаковые. Отсюда AB = AD → AB = BC, что и требовалось доказать.
Свойства треугольника
Равнобедренный треугольник относится к особому виду многоугольника. Равные его стороны называют боковыми, а отличную от них — основанием. Любую фигуру можно охарактеризовать с помощью свойств.
Признаки позволяют определить, является ли фигура равнобедренной. Из сформулированной второй теоремы следует: каждая точка, лежащая на серединном перпендикуляре, будет равноудалённой от концов боковых отрезков. Из основных свойств равнобедренного треугольника можно выделить:
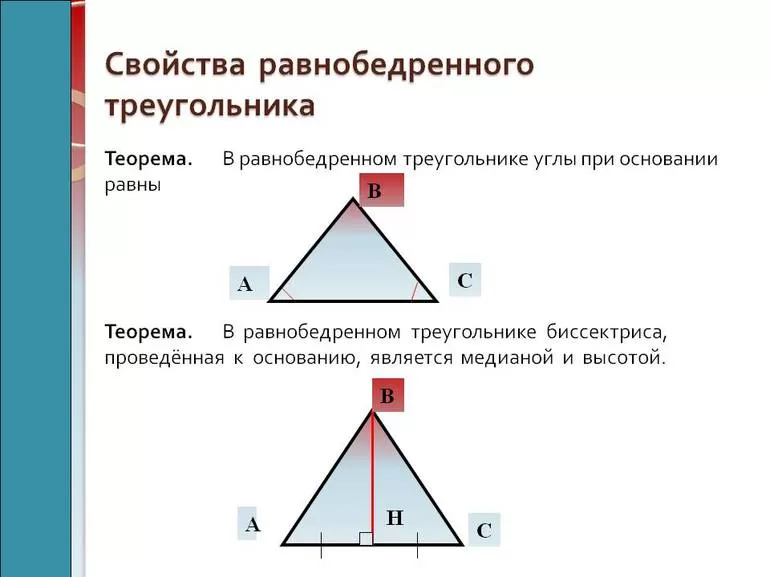
- В равнобедренной фигуре лежащие при основании углы равны. Пусть имеется треугольник AB, в котором сторона AB=BC. Нужно доказать, что угол A=C. Можно построить биссектрису BD. Из первого признака равенства: ABD = CBD. Из этого следует, что соответствующие элементы в треугольниках одинаковые, то есть, угол A равен вершине C. Теорема доказана.
- Биссектриса в равнобедренном треугольнике одновременно является медианой и высотой. Пусть есть фигура ABC, в которой AB = BC, а BD — биссектриса. Нужно доказать, что BD будет также высотой и медианой. Так как по условию дано, что 2 стороны равны, при этом BD – общая грань, угол ABD = CBD. Значит: ABD = CBD. Отсюда следует, что AD = DC, а точка D — середина отрезка AC. Следовательно BD — медиана.
А также из равенства треугольников следует, что ADB = CDB, а вершина ADC — развёрнутая. Её величина равна 1800. Значения углов, на которые она разбивается лучом DB, будет составлять 900. Таким образом, ADB = CDB = 900. Отрезок D перпендикулярен AC.
Из последнего свойства следует, что медиана является биссектрисой и высотой. Находящиеся при основании углы в равнобедренном треугольнике можно вычислить по формуле: ACB = BCA = 900 – CAB/2, где CAB — вершина, расположенная напротив основания.
Из указанных свойств следует, что точка пересечения любых замечательных линий одновременно является ортоцентром, инцентром и центром тяжести фигуры. Это важное замечание, позволяющее вычислять параметры с помощью окружности, описываемой вокруг треугольника.
Формулы и пример задания
Правильный треугольник, где все 3 стороны равны, является частным случаем равнобедренного, поэтому все формулы для поиска параметров будут одинаковыми. Самым часто используемым выражением, применяемым на уроках, является формула для поиска площади: S = (b * h)/2, где: b – основание, h – высота. Существует и более сложное равенство, позволяющее определить S, зная размеры двух прилежащих сторон: S = (b * √(a2 – (b2 / 4)) / 2.
Кроме поиска площади фигуры, в треугольнике можно вычислить:
- Периметр. Сумма всех сторон: P = a + b + c = 2ab + c.
- Высоту (медиану, биссектрису), проведённую к основанию: h 2 = b 2 − a 2 / 4.
- Соотношения между боковыми сторонами и основанием: b = 2 a*cos ( α ) , b = 2 a*sin ( β / 2).
- Стороны. Они могут быть найдены с помощью формул, выражающих их размер через другие грани и углы, значения которых известны: a = b/(2 * cos ( a )); b = a * √ (2 * (1 – cos ( b )).
- Радиус вписанной окружности. Его можно определить, зная основание и высоту: r = ( b * h )/b+* √ (4h + b 2 ); размеры боковых сторон: r = (b/2)*tg (a/2); боковые стороны и угол между ними: r = a*cos (a)*tg (a/2).
- Радиус описанного круга. Его можно найти, зная длину боковой стороны и основания по формуле: R = b/2√((2a-b)/(2a+b)).
Формулы, признаки и свойства равнобедренного треугольника важны для геометрии. Используя их, можно решать сложные задачи, связанные с многогранниками различных видов.
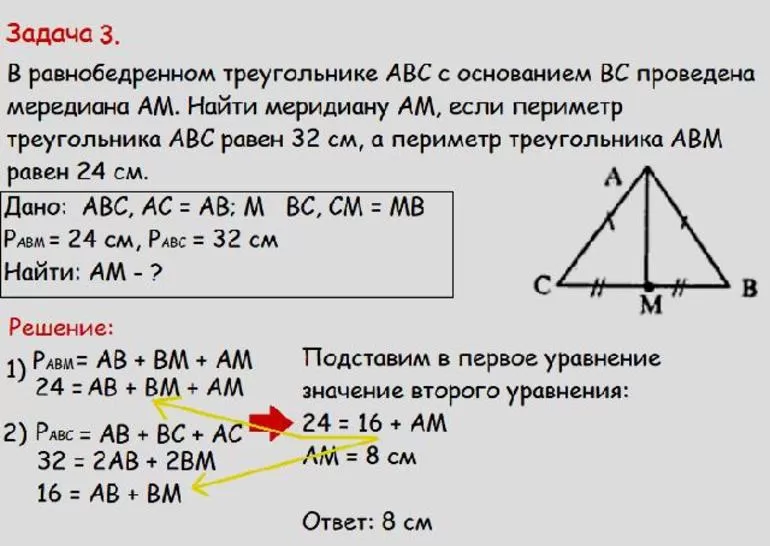
Пусть имеется равнобедренный треугольник ABC, в котором построена медиана BM. Известно, что периметр всего многоугольника 32, а фигуры ABM – 24. Нужно вычислить длину высоты. Следует понимать, что в равнобедренной фигуре медиана является высотой и биссектрисой. Сторону AB можно принять за X. Соответственно, противоположная сторона BC будет тоже равняться X. Из свойств треугольника AC разделяется в точке M на 2 одинаковых отрезка. Пусть каждый из них будет равняться Y.
По условию периметр ABC = 32, значит: 2x + 2 y = 32. Обе части равенства можно разделить на 2. В результате получится, что сумма AB и AM составляет 16. Так как периметр треугольника ABM=24, то BM = P – 16 = 24 – 16 = 8. Задача решена: длина высоты, построенная в ABC, будет равняться 8.
Источник
