Каким свойством обладает разбиение плоскости на две полуплоскости

§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.

Вопрос 3. Как обозначаются точки и прямые?
Ответ. Точки обозначаются прописными латинскими буквами: A, B, C, D, … . Прямые обозначаются строчными латинскими буквами: a, b, c, d, … .
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую a на рисунке 4 можно обозначить AC, а прямую b можно обозначить BC.
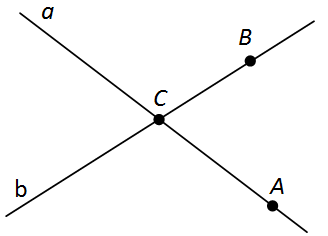
Рис.4
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
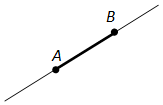
Ответ.Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: “отрезок AB”, то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Вопрос 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости.
Ответ. Прямая разбивает плоскость на две полуплоскости.
Вопрос 11. Что такое полупрямая или луч? Какие полупрямые называются дополнительными?
Ответ.Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными.
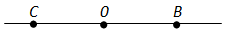
Вопрос 12. Как обозначаются полупрямые?
Ответ. Полупрямые, так же как и прямые, обозначаются строчными латинскими буквами.
Вопрос 13. Какая фигура называется углом?
Ответ. Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.
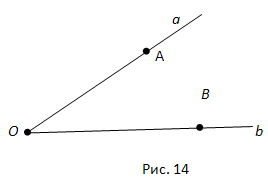
Вопрос 14. Как обозначается угол?
Ответ. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трёх точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком.
Вопрос 15. Какой угол называется развёрнутым?
Ответ. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развёрнутым.
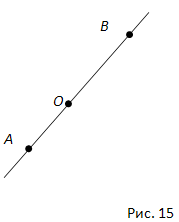
Вопрос 16. Объясните, что означает выражение: «Полупрямая проходит между сторонами угла”.
Ответ.
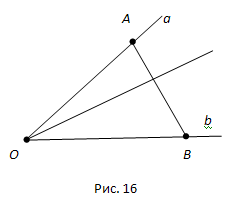
Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
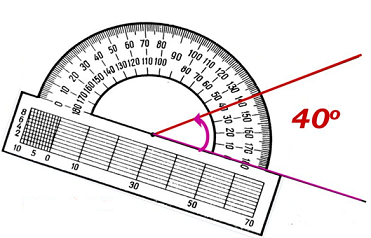
Вопрос 17. В каких единицах измеряются углы и с помощью какого инструмента? Объясните, как проводится измерение.
Ответ.Углы измеряются в градусах при помощи транспортира.
Вопрос 18. Сформулируйте основные свойства измерения углов.
Ответ. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Вопрос 19. Сформулируйте основные свойства откладывания отрезков и углов.
Ответ. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
Вопрос 20. Что такое треугольник?
Ответ.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — сторонами.

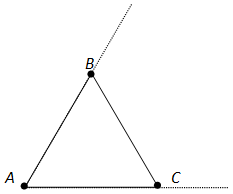
Вопрос 21. Что такое угол треугольника при данной вершине?
Ответ. Углом треугольника ABC при вершине A называется угол, образованный полупрямыми AB и AC. Так же определяются углы треугольника при вершинах B и C.
Вопрос 22. Какие отрезки называются равными?
Ответ. Отрезки называются равными, если их длины равны.
Вопрос 23. Какие углы называются равными?
Ответ. Углы называются равными, если их градусные меры равны.
Вопрос 24. Какие треугольники называются равными?
Ответ. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
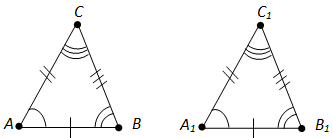
Вопрос 25. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы?
Ответ.На чертеже равные отрезки обычно отмечают одной, двумя или тремя чёрточками, а равные углы — одной, двумя или тремя дужками.
Вопрос 26. Объясните по рисунку 23 существование треугольника, равного данному.
Ответ.
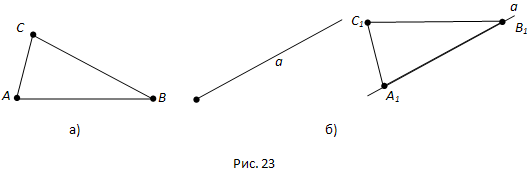
Пусть мы имеем треугольник ABC и луч a (рис. 23, а). Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча a, вершина B попала на луч a, а вершина C оказалась в заданной полуплоскости относительно луча a и его продолжения. Вершины нашего треугольника в этом новом положении обозначим A1,B1,C1 (рис. 23, б).
Треугольник A1B1C1 равен треугольнику ABC.
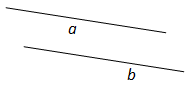
Вопрос 27. Какие прямые называются параллельными? Какой знак используется для обозначения параллельности прямых?
Ответ.Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак
Вопрос 28. Сформулируйте основное свойство параллельных прямых.
Ответ. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Вопрос 29. Приведите пример теоремы.
Ответ. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Источник
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Полуплоскости
Полуплоскости
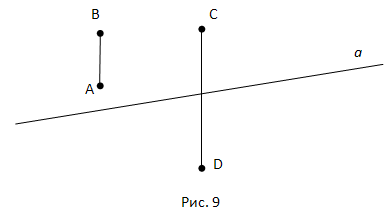
Посмотрите на рисунок 9. Прямая а разбивает плоскость на две полуплоскости. Это разбиение обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то Отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
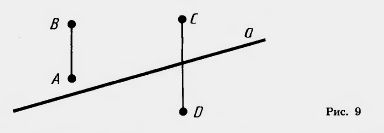
На рисунке 9 точки А и В лежат в одной из полуплоскостей, на которые прямая а разбивает плоскость. Поэтому отрезок АВ не пересекает прямую а. Точки С и D лежат в разных полуплоскостях. Поэтому отрезок CD пересекает прямую а.
Основным свойством расположения точек относительно прямой на плоскости мы будем называть следующее свойство:
IV. Прямая разбивает плоскость на две полуплоскости.
Задача (17). Даны прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее.
Пересекает ли прямую отрезок ВС? Объясните ответ.
Решение. Прямая разбивает плоскость на две полуплоскости (рис. 10).
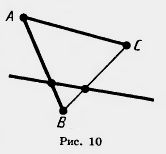
Точка А принадлежит одной из них. Отрезок АС не пересекает прямую. Значит, точка С лежит в той же полуплоскости, что и точка А.
Отрезок АВ пересекает прямую. Значит, точка В лежит в другой полуплоскости.
Таким образом, точки В и С лежат в разных полуплоскостях. А это значит, что отрезок ВС пересекает нашу прямую.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
![]() конспект урока
конспект урока
![]() опорный каркас
опорный каркас
![]() презентация урока
презентация урока
![]() акселеративные методы
акселеративные методы
![]() интерактивные технологии
интерактивные технологии
Практика
![]() задачи и упражнения
задачи и упражнения
![]() самопроверка
самопроверка
![]() практикумы, тренинги, кейсы, квесты
практикумы, тренинги, кейсы, квесты
![]() домашние задания
домашние задания
![]() дискуссионные вопросы
дискуссионные вопросы
![]() риторические вопросы от учеников
риторические вопросы от учеников
Иллюстрации
![]() аудио-, видеоклипы и мультимедиа
аудио-, видеоклипы и мультимедиа
![]() фотографии, картинки
фотографии, картинки
![]() графики, таблицы, схемы
графики, таблицы, схемы
![]() юмор, анекдоты, приколы, комиксы
юмор, анекдоты, приколы, комиксы
![]() притчи, поговорки, кроссворды, цитаты
притчи, поговорки, кроссворды, цитаты
Дополнения
![]() рефераты
рефераты
![]() статьи
статьи
![]() фишки для любознательных
фишки для любознательных
![]() шпаргалки
шпаргалки
![]() учебники основные и дополнительные
учебники основные и дополнительные
![]() словарь терминов
словарь терминов
![]() прочие
прочие
Совершенствование учебников и уроков
![]() исправление ошибок в учебнике
исправление ошибок в учебнике
![]() обновление фрагмента в учебнике
обновление фрагмента в учебнике
![]() элементы новаторства на уроке
элементы новаторства на уроке
![]() замена устаревших знаний новыми
замена устаревших знаний новыми
Только для учителей
![]() идеальные уроки
идеальные уроки
![]() календарный план на год
календарный план на год
![]() методические рекомендации
методические рекомендации
![]() программы
программы
![]() обсуждения
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Источник
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Разбиение пространства плоскостью на два полупространства
Разбиение пространства плоскостью на два полупространства
Теорема 15.4. Плоскость разбивает пространство на два полупространства. Если точки X и Y принадлежат одному полупространству, то отрезок XY не пересекает плоскость. Если же точки X uY принадлежат разным полупространствам, то отрезок XY пересекает плоскость.
Доказательство (не для запоминания). Пусть ![]() — данная плоскость. Отметим точку А, не лежащую в плоскости
— данная плоскость. Отметим точку А, не лежащую в плоскости ![]() . Такая точка существует по аксиоме C1.
. Такая точка существует по аксиоме C1.
Разобьем все точки пространства, не лежащие в плоскости ![]() , на два полупространства следующим образом. Точку X отнесем к первому полупространству, если отрезок АХ не пересекает плоскость
, на два полупространства следующим образом. Точку X отнесем к первому полупространству, если отрезок АХ не пересекает плоскость ![]() , и ко второму полупространству, если отрезок АХ пересекает плоскость
, и ко второму полупространству, если отрезок АХ пересекает плоскость ![]() . Покажем, что это разбиение пространства обладает свойствами, указанными в теореме.
. Покажем, что это разбиение пространства обладает свойствами, указанными в теореме.
Пусть точки X и Y принадлежат первому полупространству. Проведем через точки А, X и Y плоскость ![]() , . Если плоскость
, . Если плоскость ![]() , не пересекает плоскость
, не пересекает плоскость ![]() , то отрезок XY тоже не пересекает эту плоскость.
, то отрезок XY тоже не пересекает эту плоскость.
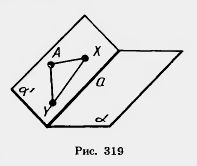
Допустим, что плоскость ![]() , пересекает плоскость
, пересекает плоскость ![]() ( рис. 319). Так как плоскости различны, то их пересечение происходит по некоторой прямой а.
( рис. 319). Так как плоскости различны, то их пересечение происходит по некоторой прямой а.
Прямая а разбивает плоскость ![]() , на две полуплоскости. Точки X и Y принадлежат одной полуплоскости, именно той, в которой лежит точка А.
, на две полуплоскости. Точки X и Y принадлежат одной полуплоскости, именно той, в которой лежит точка А.
Поэтому отрезок XY не пересекает прямую а, а значит и плоскость ![]() .
.
Если точка X и Y принадлежат второму полупространству, то плоскость ![]() , заведомо пересекает плоскость
, заведомо пересекает плоскость ![]() , так как отрезок АХ пересекает плоскость а.
, так как отрезок АХ пересекает плоскость а.
Точки X и Y принадлежат одной полуплоскости разбиением плоскости ![]() , прямой а. Следовательно отрезок XY не пересекает прямую а, значит и плоскость
, прямой а. Следовательно отрезок XY не пересекает прямую а, значит и плоскость ![]() .
.
Если , наконец, точка Х пренадлежит одному полупространству, а точка Y – другому, то плоскость ![]() , пересекает плоскость
, пересекает плоскость ![]() , а точки X и Y лежат в разных полуплоскостях плоскости
, а точки X и Y лежат в разных полуплоскостях плоскости ![]() , относительно прямой а. Поэтому отрезок XY пересекает прямую а, а значит и плоскость
, относительно прямой а. Поэтому отрезок XY пересекает прямую а, а значит и плоскость ![]() . Теорема доказана.
. Теорема доказана.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
![]() конспект урока
конспект урока
![]() опорный каркас
опорный каркас
![]() презентация урока
презентация урока
![]() акселеративные методы
акселеративные методы
![]() интерактивные технологии
интерактивные технологии
Практика
![]() задачи и упражнения
задачи и упражнения
![]() самопроверка
самопроверка
![]() практикумы, тренинги, кейсы, квесты
практикумы, тренинги, кейсы, квесты
![]() домашние задания
домашние задания
![]() дискуссионные вопросы
дискуссионные вопросы
![]() риторические вопросы от учеников
риторические вопросы от учеников
Иллюстрации
![]() аудио-, видеоклипы и мультимедиа
аудио-, видеоклипы и мультимедиа
![]() фотографии, картинки
фотографии, картинки
![]() графики, таблицы, схемы
графики, таблицы, схемы
![]() юмор, анекдоты, приколы, комиксы
юмор, анекдоты, приколы, комиксы
![]() притчи, поговорки, кроссворды, цитаты
притчи, поговорки, кроссворды, цитаты
Дополнения
![]() рефераты
рефераты
![]() статьи
статьи
![]() фишки для любознательных
фишки для любознательных
![]() шпаргалки
шпаргалки
![]() учебники основные и дополнительные
учебники основные и дополнительные
![]() словарь терминов
словарь терминов
![]() прочие
прочие
Совершенствование учебников и уроков
![]() исправление ошибок в учебнике
исправление ошибок в учебнике
![]() обновление фрагмента в учебнике
обновление фрагмента в учебнике
![]() элементы новаторства на уроке
элементы новаторства на уроке
![]() замена устаревших знаний новыми
замена устаревших знаний новыми
Только для учителей
![]() идеальные уроки
идеальные уроки
![]() календарный план на год
календарный план на год
![]() методические рекомендации
методические рекомендации
![]() программы
программы
![]() обсуждения
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Источник
Похожие вопросы:

Геометрия, 17.03.2019 07:50
Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответов: 1

Другие предметы, 17.04.2019 02:40
Сформулируйте, какими свойствами обладает сера и какими — железо.
Ответов: 2

Геометрия, 20.05.2019 19:00
Какими свойствами обладает деление плоскости на две полуплоскости?
Ответов: 2

Математика, 25.05.2019 03:30
Сформулируйте, какими свойствами обладает сера и какими – железо
Ответов: 2

Химия, 25.05.2019 09:00
Сформулируйте, какими свойствами обладает сера и какими
Ответов: 2

Геометрия, 25.05.2019 16:00
1.назовите основные фигуры на плоскости. 2.сформулируйте основное свойство расположения точек на прямой. 3.какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответов: 1

Геометрия, 12.06.2019 05:40
1)какая фигура называется четырехугольником? 2)что такое вершины, углы стороны диагонали периметр четырехугольника? 3)какие углы стороны четырехугольник называется выпуклым? 4)чему равна сумма углов выпуклого четырехугольника? 5)какой четырех угольник называется выпуклым? 6)какой четырех угольник называют параллелограмм? 7)какими свойствами обладает параллелограмм? 8)назовите признаки параллелограмма. 9)сформулируйте свойства прямоугольника. 10)какой четырехугольник называется квадратом? 11)сформулируйте свойства ромба. 12)какой четырехугольник называется ромбом? 13)какой четырехугольник называется прямоугольником? 14)какими свойствами обладает квадрат? ответьте
Ответов: 3

Геометрия, 30.06.2019 09:30
Какими свойствами обладает разбиение плоскости на 2 полуплоскости?
Ответов: 3

Биология, 03.08.2019 13:50
Все читали сказку одолень трава . напишите какими сказочными свойствами обладает растение и какими свойствами обладает растение в реальном мире .
Ответов: 1

Геометрия, 09.09.2019 18:00
1какой многоугольник называется выпуклым ? как найти сумму углов выпуклого n угольника? 2 какая фигура называется параллелограммом? какими свойствами он обладает? 3 сформулируйте признаки параллелограмма. 4 какая фигура называется ромбом, квадратом, трапецией ? какими свойствами они ? 5 какими свойствами обладает равнобедренная трапеция? 6 сформулируйте основные свойства площадей многоугольников как найти площадь прямоугольника, квадрата? 7 как найти площадь параллелограмма, треугольника, ромба, трапеции? 8 сформулируйте теорему пифагора и теорему обратную теореме пифагора
Ответов: 2

Химия, 30.09.2019 06:10
:какой оксид обладает более кислотными свойствами: а)p2o5 или so3; б) seo3 или teo3? какими свойствами гидроксиды: lioh, be(oh)2, h3aso4? какой гидроксид обладает более основными свойствами: ba(oh)2 или sr(oh)2?
Ответов: 1

Химия, 03.10.2019 21:42
1. сравните силу кислот h2so2 и н2so3 и оснований fe(oh)2 и fe(oh)3
2. придумайте какими свойствами обладает элемент 1-й группы калий, его оксид. укажите характер его оксида возможные и свойства простого вещества.
3. придумайте какими свойствами обладает элемент 4-й группы германий, его оксид.
Ответов: 3
У тебя есть свой ответ?
1) какими свойствами обладает разбиение плоскости на 2 полуплоскости? 2)сформулируйте основное свой…
Отправлено
Вопросы по другим предметам:

Литература, 18.06.2020 09:33

Литература, 18.06.2020 09:33

Геометрия, 17.06.2020 21:25

Математика, 17.06.2020 21:04

Математика, 17.06.2020 21:04

Математика, 17.06.2020 21:29

Русский язык, 17.06.2020 21:28



Другие предметы, 17.06.2020 09:40
Источник
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Прямые и точки, размещенные в пространстве, мы будем обозначать аналогично размещенным на плоскости – с помощью строчных и прописных латинских букв (B, A, d, q и др.) Если в условиях задачи у нас есть две точки, которые расположены на прямой, то можно выбрать такие обозначения, которые будут соответствовать друг другу, например, прямая DB и точки D и B.
Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α, γ или π.
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
Определение 1
В любой плоскости есть точки.
Такой вариант расположения также называется прохождением плоскости через точку. Чтобы обозначить это на письме, используется символ ∈. Так, если нам нужно записать в буквенном виде, что через точку A проходит некая плоскость π, то мы пишем: A∈π.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Определение 2
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Зная это правило, можно ввести новое обозначение плоскости. Вместо маленькой греческой буквы мы можем использовать названия точек, лежащих в ней, например, плоскость АВС.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Определение 3
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Выше мы уже отмечали, что для обозначения плоскости в пространстве будет достаточно трех точек, а четвертая может находиться как в ней, так и вне ее. Если нужно обозначить отсутствие принадлежности точки к заданной плоскости на письме, то используется знак ∉. Запись вида A∉π правильно читается как «точка A не принадлежит плоскости π»
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
Определение 4
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Чтобы записать принадлежность прямой некой плоскости, используем тот же символ, что и для точки. Если мы напишем «a∈π», то это будет означать, что у нас есть прямая a, которая расположена в плоскости π. Изобразим это на рисунке:
Второй вариант взаимного расположения – это когда прямая пересекает плоскость. В таком случае у них будет всего одна общая точка – точка пересечения. Для записи такого расположения в буквенном виде используем символ ∩. Например, выражение a∩π=M читается как «прямая a пересекает плоскость π в некоторой точке M». Если у нас есть точка пересечения, значит, у нас есть и угол, под которым прямая пересекает плоскость.
Графически этот вариант расположения выглядит так:
Если у нас есть две прямые, одна из которых лежит в плоскости, а другая ее пересекает, то они являются перпендикулярными друг другу. На письме это обозначается символом ⊥. Особенности такой позиции мы рассмотрим в отдельной статье. На рисунке это расположение будет выглядеть следующим образом:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
Определение 5
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Третий случай взаимного расположения прямой и плоскости – это их параллельность. В таком случае ни одной общей точки у них нет. Для указания таких отношений на письме используется символ ∥. Если у нас есть запись вида a∥π, то ее следует читать так: «прямая a является параллельной плоскости ∥». Подробнее этот случай мы разберем в статье про параллельные плоскости и прямые.
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Определение 6
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Определение 7
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
Определение 8
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна ?
