Каким свойством обладает точка пересечения медиан треугольника
Привет!
Сегодня мы рассмотрим часть треугольника, которая не раз поможет тебе при решении многих задач, — медиану.
Эта приятная, лёгкая и полезная теория!
Поехали!
ШПОРА ПО МЕДИАНЕ ТРЕУГОЛЬНИКА
1. Медиана делит сторону пополам.
Медиана — линия, проведенная из вершины треугольника к середине противоположной стороны.
2. Теорема: медиана делит площадь пополам
( displaystyle {{S}_{Delta ABM}}=frac{1}{2}~AMcdot BH;)( displaystyle {{S}_{Delta BMC}}=frac{1}{2}~CMcdot BH)
Но ( displaystyle AM=CM), значит,
( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}})
3. Три медианы треугольника
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.( displaystyle {{S}_{Delta ABM}}=frac{1}{2}~AMcdot BH;)
( displaystyle {{S}_{Delta BMC}}=frac{1}{2}~CMcdot BH)
Но ( displaystyle AM=CM), значит,
( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}})
4. Формула длины медианы
( displaystyle {{m}^{2}}=frac{1}{4}~left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} right))
5. Медиана в прямоугольном треугольнике
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Обратная теорема: если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.
НАЧАЛЬНЫЙ УРОВЕНЬ
Определение медианы
Это очень просто!
Возьми треугольник:
Отметь на какой-нибудь его стороне середину ( displaystyle M).
И соедини с противоположной вершиной!
Получившаяся линия ( displaystyle BM) и есть медиана.
Медиана –линия, проведённая из вершины треугольника к середине противоположной стороны.
Свойства медианы
Какие же хорошие свойства есть у медианы?
1) Вот представим, что треугольник ( displaystyle ABC) – прямоугольный. Бывают же такие, верно?
Тогда медиана равна половине гипотенузы!
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник. Зачем, спросишь?
А вот ты ходишь по Земле – ты видишь, что она круглая? Нет, конечно, для этого на Землю нужно смотреть из космоса. Вот и мы посмотрим на наш прямоугольный треугольник «из космоса».
Итак, рассмотрим прямоугольник ( displaystyle ABCD).
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD):
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»)
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC).
Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, “капканы” – все там.
Регистрируйся здесь и приходи!
Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В ( displaystyle Delta ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN). Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем, это если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
( AB=13)
Вот и ответ!
2) А теперь пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении ( 2:1), считая от вершины.
Сложно? Смотри на рисунок:
Медианы ( displaystyle AM), ( displaystyle BN) и ( displaystyle CK) пересекаются в одной точке.
И… ( доказываем это в следующем уровне теории, а пока запомни!):
- ( displaystyle AO) – вдвое больше, чем ( displaystyle OM);
- ( displaystyle BO) – вдвое больше, чем ( displaystyle ON);
- ( displaystyle CO) – вдвое больше, чем ( displaystyle OK).
Не устал ещё? На следующий пример сил хватит? Сейчас мы применим всё, о чём говорили!
Задача:
В треугольнике ( displaystyle ABC) проведены медианы ( displaystyle BM) и ( displaystyle AK), которые пересекаются в точке ( displaystyle O). Найти ( displaystyle BO), если ( displaystyle AB=3;text{ }BC=4,text{ }angle B=90{}^circ .)
Решаем:
Решение:
( displaystyle angle B=90{}^circ ) – треугольник прямоугольный!
Значит, ( BM=frac{AC}{2}).
(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).
Найдём ( displaystyle AC) по теореме Пифагора:
( A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}=9+16=25)
( AC=5)
Значит, ( BM=frac{AC}{2}=frac{5}{2}).
А теперь применим знания про точку пересечения медиан.
Давай обозначим ( displaystyle OM=x). Отрезок ( BO=2OM=2x), а ( BM=3x). Если не все понятно – посмотри на рисунок.
Мы уже нашли, что ( BM=frac{5}{2}).
Значит, ( 3x=frac{5}{2}); ( x=frac{5}{6}).
В задаче нас спрашивают об отрезке ( displaystyle BO).
В наших обозначениях ( BO=2x=frac{5}{6}cdot 2).
Значит, ( BO=frac{5}{3}).
Ответ: ( BO=frac{5}{3}).
Понравилось? Старайся теперь сам применять знания про медиану!
Нравится учебник?
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, там еще круче!
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
СРЕДНИЙ УРОВЕНЬ
Определение медианы
Медиана – линия, проведенная из вершины треугольника к середине противоположной стороны.
Посмотри на рисунок. Линия ( displaystyle BM) – медиана.
Итак,
Медиана делит сторону пополам.
И все? А может, она ещё что-нибудь делит пополам? Представь себе, что это так!
Теорема о площади
Медиана делит площадь пополам.
Почему? А давай вспомним самую простую форму площади треугольника.
( S=frac{1}{2}a~cdot h)
И применим эту формулу аж два раза!
Зарегистрируйся один раз и ты откроешь все 100 статей учебника
А также получишь доступ к видеоурокам и другим бесплатным материалам курса “Подготовка к ЕГЭ с репетитором”
* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент
Посмотри, медиана ( displaystyle BM) разделила ( displaystyle triangle ABC) на два треугольника: ( displaystyle triangle ABM) и ( displaystyle triangle BMC). Но! Высота-то у них одна и та же – ( displaystyle BH)!
Только в ( displaystyle triangle ABM) эта высота ( displaystyle BH) опускается на сторону ( displaystyle AM), а в ( displaystyle triangle BMC) – на продолжение стороны ( displaystyle CM). Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу ( S=frac{1}{2}a~cdot h).
1) B ( displaystyle triangle ABM):
“( displaystyle a)” – это ( displaystyle AM) | ( displaystyle Rightarrow {{S}_{triangle ABM}}=frac{1}{2}~AM~cdot BH) |
2) B ( displaystyle triangle BMC):
“( displaystyle a)” – это ( displaystyle CM) | ( displaystyle Rightarrow {{S}_{triangle BMC}}=frac{1}{2}~CM~cdot BH) |
Запишем ещё раз:
( displaystyle {{S}_{triangle ABM}}=frac{1}{2}~AM~cdot BH); ( displaystyle {{S}_{triangle BMC}}=frac{1}{2}~CM~cdot BH)
Но ( displaystyle AM=CM)! (Посмотри на рисунок или вспомни, что ( displaystyle BM) – медиана).
Значит, ( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}}) – площадь ( displaystyle triangle ABC) разделилась на две равные части. Ура! Доказали теорему. И получилось совсем несложно – всего-то одна формула площади.
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, “капканы” – все там.
Регистрируйся здесь и приходи!
Три медианы треугольника
Теорема.
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.
Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
Первое утверждение: медианы пересекаются в одной точке.
Второе утверждение: точкой пересечения медианы делятся в отношении ( displaystyle 2:1 ), считая от вершины.
Давай попробуем разгадать секрет этой теоремы:
Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой ( displaystyle E).
Соединим точки ( displaystyle N) и ( displaystyle K). Что получилось?
Конечно, ( displaystyle NK) – средняя линяя ( displaystyle triangle ABC). Ты помнишь, что это значит?
1
( displaystyle NK) параллельна ( displaystyle AC);
2
( displaystyle NK=frac{AC}{2}).
А теперь проведем ещё одну среднюю линию: отметим середину ( displaystyle AE) – поставим точку ( displaystyle F), отметим середину ( displaystyle EC) – поставим точку ( displaystyle G).
Теперь ( displaystyle FG) – средняя линия ( displaystyle triangle AEC). То есть:
1
( displaystyle FG) параллельна ( displaystyle AC);
2
( displaystyle FG=frac{AC}{2}).
Заметил совпадения? И ( displaystyle NK) , и ( displaystyle FG) – параллельны ( displaystyle AC). И ( displaystyle NK=frac{AC}{2}), и ( displaystyle FG=frac{AC}{2}).
Что из этого следует?
- ( displaystyle NK) параллельна ( displaystyle FG);
- ( displaystyle NK=FG)
Посмотри теперь на четырехугольник ( displaystyle NKGF). У какого четырехугольника противоположные стороны (( displaystyle NK) и ( displaystyle FG)) параллельны и равны?
Конечно же, только у параллелограмма!
Значит, ( displaystyle NKGF) – параллелограмм. Ну и что? А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
Получилось, что
- ( displaystyle AF=FE) (мы так выбирали точку ( displaystyle F))
- ( displaystyle FE=EK) (из-за того, что ( displaystyle NKGF) – параллелограмм)
То есть ( displaystyle AF=FE=EK) – медиана ( displaystyle AK) разделена точками ( displaystyle F) и ( displaystyle E) на три равные части. И точно так же ( displaystyle CG=GE=EN).
Значит, точкой ( displaystyle E) обе медианы разделились именно в отношении ( displaystyle 2:1), то есть ( displaystyle AE=2EK) и ( displaystyle CE=2NE).
Что же будет происходить с третьей медианой? Давай вернемся в начало. О, ужас?! Нет, сейчас будет все гораздо короче. Давай выбросим медиану ( displaystyle CN) и проведем медианы ( displaystyle AK) и ( displaystyle BM).
А теперь представим, что мы провели точно такие же рассуждения, как для медиан ( displaystyle AK) и ( displaystyle CN). Что тогда?
Получится, что медиана ( displaystyle BM) разделит медиану ( displaystyle AK) абсолютно точно так же: в отношении ( displaystyle 2:1), считая от точки ( displaystyle A).
Но сколько же может быть точек на отрезке ( displaystyle AK), которые делят его в отношении ( displaystyle 2:1), считая от точки ( displaystyle A)?
Конечно же, только одна! И мы её уже видели – это точка ( displaystyle E).
Что же получилось в итоге?
Медиана ( displaystyle BM) точно прошла через ( displaystyle E)! Все три медианы через неё прошли. И все разделились в отношении ( displaystyle 2:1), считая от вершины.
Вот и разгадали (доказали) теорему. Разгадкой оказался параллелограмм, сидящий внутри треугольника.
Нравится учебник?
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, там еще круче!
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
Формула длины медианы
Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно? Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем.
Итак, ( displaystyle {{m}^{2}}=frac{1}{4}~left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} right))
Медиана в прямоугольном треугольнике
Теорема.
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Как бы понять, отчего так выходит?
Давай смотреть внимательно. Только не на треугольник, а на прямоугольник.
Итак, рассмотрим прямоугольник ( displaystyle ABCD).
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD)
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, …»)
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC). Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить подумай сам: разве бывает какой – нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике. Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В ( displaystyle triangle ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN). Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем: если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
( AB=13)
Вот и ответ!
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Второе, заниматься по системе – иначе у тебя уйдет много времени и ты, что-нибудь пропустишь.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Источник
Медиана – это один из уникальных отрезков треугольника. Медиана имеет ряд свойств, полезных для решения задач, а точка пересечения медиан еще больше расширяет список этих свойств. О точке пересечения медиан, ее свойствах и пойдет речь сегодня.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики – более 33 лет.

Медиана
Медиана – это отрезок, соединяющий вершину треугольника с серединой отрезка противоположной стороны. Три медианы треугольника пересекаются в одной точке, которая зовется точкой пересечения медиан.
Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь отрезок медианы соединяет вершину и середину стороны. А середина стороны всегда лежит внутри треугольника.
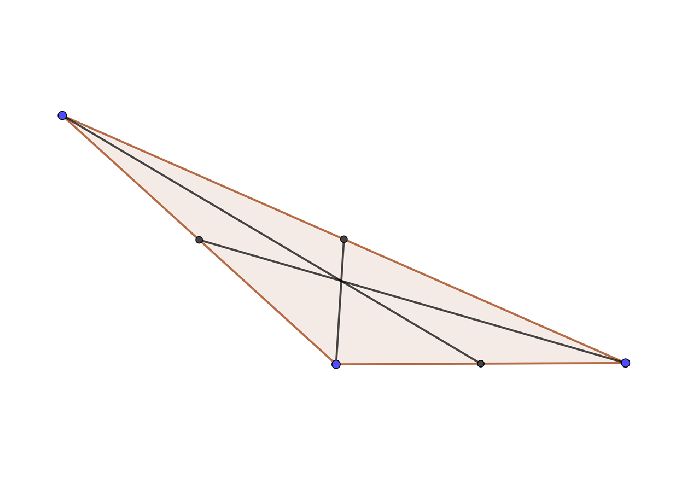
Рис. 1. Медианы в тупоугольном треугольнике.
Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2
Есть еще одно любопытное свойство медиан, которое позволит не запутаться при построении золотого сечения треугольника. Медиана в треугольнике всегда располагается между высотой и биссектрисой (исключение – равнобедренный и равносторонний треугольники).
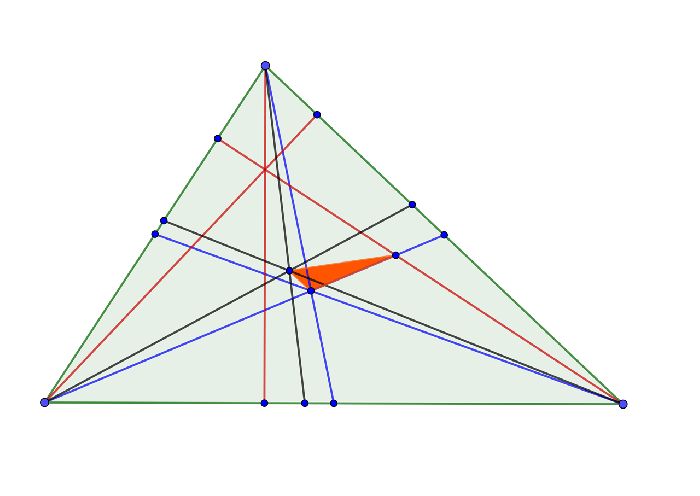
Рис. 2. Золотое сечение произвольного треугольника.
Приведем формулу вычисления длины медианы по трем сторонам. Эта формула часто используется при решении задач, и потому ее желательно запомнить.
$$m_c={{sqrt{2a^2+2b^2-c^2}}over{2}}$$
Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.
Точка пересечения медиан
Точка пересечения медиан является одной из 3 замечательных точек треугольника, которые составляют золотое сечение треугольника.
Точка пересечения медиан треугольника имеет ряд свойств, полезных при решении задач:
- Медиана точкой пересечения делится на отрезки в отношении 2:1 считая от вершины.
- Три медианы, проведенные в треугольнике, делят его на 6 равновеликих треугольников. Равновеликими называют треугольники с равной площадью. Сами по себе эти фигуры имеют мало общего, но численная характеристика площади у них совпадает.
- Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.
Точка пересечения медиан единственная из золотого сечения треугольника, имеет реальный физический смысл. Если из картона вырезать треугольник, тонким карандашом провести в нем медианы, то точка их пересечения будет центром тяжести плоской фигуры.
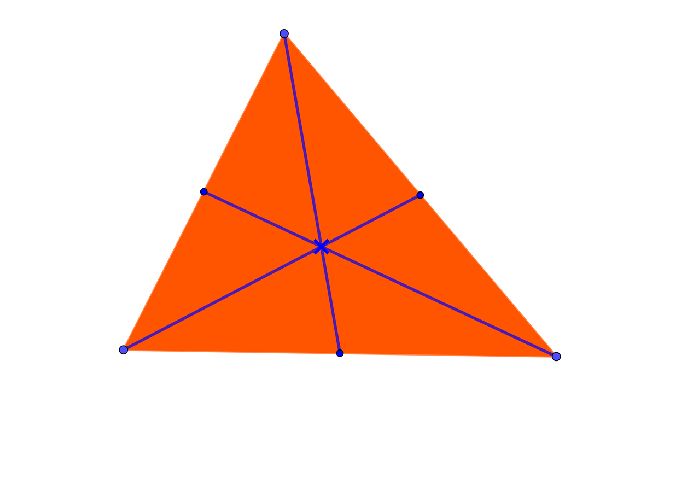
Рис. 3. Центр тяжести треугольника.
Это значит, что если установить иголку в эту точку, то фигура будет держаться на ней без прокола, исключительно за счет равновесия.
Что мы узнали?
Мы привели формулу вычисления медианы по 3 сторонам треугольника. Привели несколько свойств точки пересечения медиан в треугольнике. Поговорили о реальном физическом значение центроида треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
Средняя оценка: 4.1. Всего получено оценок: 140.
Источник
Процесс решения задачи по геометрии существенно упрощается при использовании теорем и следствий. Одной из них является утверждение о точке пересечения медиан треугольника, доказательство которой необходимо рассмотреть подробно. Специалисты в математической сфере рекомендуют изучить теоретические аспекты, а затем переходить для их закрепления к практике.
Общие сведения
Перед доказательством теорем необходимо ознакомиться с основными понятиями. Прямой называется совокупность точек, расположенных в одной плоскости, через которые можно провести линию без искажений в пространстве. Отрезок — часть прямой, ограниченной правой и левой границами.
Треугольник (обозначается «Δ») — геометрическая фигура, состоящая из трех сторон и вершин. Предпоследние являются отрезками, а последние — точками, не лежащими на одной прямой и соединяющими стороны между собой. Следует отметить, что треугольники бывают нескольких типов. К ним относятся следующие:
Первая группа состоит из сторон различной длины. При двух эквивалентных между собой сторонах фигура является равнобедренной. Обязательным условием для третьей группы считается равенство всех сторон. Кроме того, фигуры делятся по типу градусных мер таким образом:
Остроугольным называется треугольник, у которого углы (в задачах обозначается символом «∠ «) меньше 90 градусов.
Если у него один из ∠ эквивалентен 90, то этот признак свидетельствует о принадлежности его ко второму типу. Когда у фигуры хотя бы один из ∠ больше 90, тогда он принадлежит к третьему виду.
Понятие дополнительных отрезков
У любого Δ существуют дополнительные отрезки, которые используются при решении задач по геометрии. К ним относятся следующие: медиана, биссектриса и высота. Они существенно отличаются между собой в произвольных треугольниках, а также совпадают в равнобедренных и правильных геометрических телах.
Медиана (М) — некоторый отрезок, исходящий из вершины на середину стороны. Иными словами, любой геометрический элемент, опущенный из вершины на среднюю точку, является медианой. Последних в треугольнике может быть не более трех.
Биссектриса (Б) — часть прямой, которая делит угол на два равных компонента. В любом треугольнике можно провести всего три таких отрезка. Высота (В) — перпендикуляр, опущенный из вершины на противоположную сторону. Следует отметить, что высоты бывают внешними и внутренними. Первые проводятся из вершины на проекцию Δ, а вторые находятся внутри фигуры. В каждом треугольнике можно провести определенное количество дополнительных отрезков:
Во втором случае М, В и Б совпадают между собой только один раз, а в последнем — полное сходство, поскольку медианы являются биссектрисами и высотами. Их точка пересечения — центр треугольника. Далее следует перейти к непосредственному доказательству теорем.
Теорема о взаимном пересечении
Первую базовую теорему, которую следует разобрать, имеет такую формулировку: медианы любого треугольника пересекаются в одной точке, которая является центром фигуры. Ее доказательство осуществляется по такому алгоритму:
Аналогично можно доказать, что медиана UU’ также пересекается с SS’ и TT’ в точке F. Для этой цели необходимо начертить еще один треугольник с таким же обозначением, т. е. ΔSTU.
После этого выполнить все пять пунктов алгоритма, но для медиан SS’ и UU’. Затем сопоставить два доказательства для получения общей формулировки.
Утверждения о соотношении
Однако для решения задач одной теоремы о пересечении медиан недостаточно. Математики доказали несколько других утверждений, которые могут быть полезными при нахождении неизвестных величин. Первая из них гласит, что точка, в которой пересекаются медианы, пропорционально делит медианы 2:1 относительно вершины. Для доказательства утверждения необходимо воспользоваться такой методикой:
Следующим полезным утверждением является формула, позволяющая найти длину медианы. Она в словесном эквиваленте звучит таким образом: длина равна квадратному корню из суммы половины квадратов двух других сторон, не принадлежащих ей, без четвертой части квадрата стороны, на которую она опущена. Для доказательства рекомендуется использовать такой алгоритм:
Теорема имеет следствие, представленное в виде соотношения, позволяющее выявить взаимосвязь между сторонами и медианами. Оно имеет такой вид: (М{u})^2 + (М{s})^2 + (М{t})^2=3/4(s^2+t^2+u^2).
Координаты точки
При решении задач очень часто необходимо находить координаты точки пересечения медиан произвольного ΔSTU. Доказательство или выведение этой формулы является очень сложным. Однако математики решили данную проблему. Они предлагают использовать уже готовое соотношение, состоящее из двух компонентов:
Вышеописанные формулы рекомендуется применять, когда требуется определить координаты точек без чертежа. Специалисты на ранних этапах обучения рекомендуют размещать треугольник в прямоугольной декартовой системе координат. После этого отмечать каждую вершину с заданными координатами, а затем проводить медианы.
Для нахождения величины абсциссы и ординаты нужно из искомой точки опускать перпендикуляры на последние.
Нахождение координаты будет очень простым и удобным. Кроме того, в интернете существует множество приложений для этих целей. Они называются онлайн-калькуляторами.
Иногда встречаются задания со следующей формулировкой: выведите формулы, выражающие координаты точки пересечения медиан, с исходными данными (вершинами или сторонами). Для этого рекомендуется просто подставить искомые значения в соответствующие формулы нахождения абсциссы и ординаты.
Полезные свойства
Математики для облегчения учебы вывели важные свойства медианы. К ним относятся следующие:
На координатной плоскости, руководствуясь первым свойством, чертится треугольник. После этого требуется провести две медианы, обозначив общую точку (где они пересекаются). Далее необходимо поставить в нее иголку циркуля, и начертить
