Каким свойством обладает внешний угол треугольника

Основные определения
Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:
- угла и треугольника;
- смежных углов;
- параллельных прямых.
Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.
Определение 1
Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.
На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.
Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ
Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Теорема о сумме углов треугольника
Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:
Теорема 1
Сумма углов треугольника равна $180^{circ}$.
Приведём её доказательство.
Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.
Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.
Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Видим, что углы 1 и 5 – накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.
Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.
Внешний угол треугольника
В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:
Определение 2
Внешний угол треугольника – это угол, являющийся смежным с каким-нибудь углом данного треугольника.
Имеем теорему:
Теорема 2
Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.
Докажем эту теорему.
Рассмотрим следующий рисунок:
Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ
Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:
$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.
Рассмотрим пример задачи на данную тему.
Пример 1
Задача. $triangle ABC$ – равнобедренный. $AC$ – основание этого треугольника. $AC$=37 см, внешний угол при $B$ равняется $60^{circ}$. Нужно найти расстояние от точки $C$ до прямой $AB$.
Решение. Сделаем рисунок:
Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ
На рисунке прямая, обозначающая расстояние от точки $C$ до прямой $AB$ обозначена как $CD$. В математике такое расстояние называют высотой. По определению высоты треугольника, прямая высоты перпендикулярна той стороне, на которую опущена. То есть $angle ADC = 90^{circ}$.
По теореме о внешнем угле треугольника находим $angle B$: $angle B=180-60=120^{circ}$. По теореме о сумме углов треугольника получается, что $angle A + angle C = 180-120=60$. Так как треугольник равнобедренный, углы у основания равны по $30^{circ}$.
Рассмотрим $triangle ADC$. Из вышеуказанного следует, что он прямоугольный. Из свойства прямоугольных треугольников известно, что катет такого треугольника, который лежит против угла $30^{circ}$, равен половине гипотенузы. В нашем случае, $СD$ является катетом против угла $30^{circ}$, а $AC$ – гипотенуза. Поэтому справедливо утверждать, что $CD=37/2=18,5$ см.
Ответ: 18,5 см.
Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.
Источник
Ðåçóëüòàò ñëîæåíèÿ äâóõ âíóòðåííèõ óãëîâ òðåóãîëüíèêà áóäåò ðàâíÿòüñÿ âíåøíåìó óãëó, íå ñìåæíîìó ñ íèìè.
Ïðîàíàëèçèðóåì óãëû ïðîèçâîëüíîãî òðåóãîëüíèêà ÀÂÑ.
Êàê èçâåñòíî, ñóììà âñåõ óãëîâ òðåóãîëüíèêà 2 d, èç ýòîãî ïîëó÷àåì òîæäåñòâî / 1 + / 2 = 2d – / 3, íî è / ÂÑD, âíåøíèé óãîë ýòîãî òðåóãîëüíèêà, íå ñìåæíûé ñ / 1 è / 2, â ñâîþ î÷åðåäü ìîæíî âûðàçèòü òîæäåñòâîì 2d — / 3.
Èç ýòîãî ìîæíî ñäåëàòü âûâîä:
/ 1 + / 2 = 2d — / 3;
/ ÂÑD = 2d — / 3.
Çíà÷èò âåðíûì áóäåò / 1 + / 2 = / ÂÑD.
Óñòàíîâëåííîå ñâîéñòâî âíåøíåãî óãëà òðåóãîëüíèêà êîíêðåòèçèðóåò ôîðìóëèðîâêó òåîðåìû î âíåøíåì óãëå òðåóãîëüíèêà, â êîòîðîé îáîñíîâûâàëîñü ëèøü, ÷òî âíåøíèé óãîë òðåóãîëüíèêà áîëüøå âñÿêîãî âíóòðåííåãî óãëà òðåóãîëüíèêà, íå ñìåæíîãî ñ íèì; òåïåðü æå ïîäòâåðæäåíî, ÷òî âíåøíèé óãîë ðàâíÿåòñÿ ñóììå îáîèõ âíóòðåííèõ óãëîâ, íå ñìåæíûõ ñ íèì.
Ðàñ÷åò òðåóãîëüíèêà îíëàéí | |
| Ðàñ÷åò âñåõ óãëîâ, ñòîðîí è ïëîùàäè ïî èçâåñòíûì óãëàì è ñòîðîíàì òðåóãîëüíèêà, ÷åðòåæ òðåóãîëüíèêà | |
| Ðàñ÷åò òðåóãîëüíèêà îíëàéí | |
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Òðåóãîëüíèê | |
| Òðåóãîëüíèê, ñòîðîíû, óãëû, âûñîòà òðåóãîëüíèêà, ìåäèàíû, áèññåêòðèñû. Ïðÿìîóãîëüíûé òðåóãîëüíèê, ïëîùàäü òðåóãîëüíèêà. | |
| Òðåóãîëüíèê | |
Òèïû òðåóãîëüíèêîâ. | |
| Íåêîòîðûé òðåóãîëüíèê, â êîòîðîì âñå ñòîðîíû íå îäèíàêîâîé äëèíû, ïðèíÿòî íàçûâàòü ðàçíîñòîðîííèìè. | |
| Òèïû òðåóãîëüíèêîâ. | |
Источник
Цели.
Знакомство учащихся с понятием внешнего угла
треугольника, с формулировкой определения;
рассмотреть свойство внешнего угла
треугольника; закрепить знания учащихся о сумме
углов треугольника и о внешнем угле треугольника
при решении задач.
Задачи.
1. Обучающая: обеспечить усвоение
материала всеми учащимися; учить и научить
каждого ученика самостоятельно добывать знания;
формировать навыки, умения, которые обеспечивают
успешное выполнение деятельности.
2. Развивающая: способствовать
развитию математического кругозора, мышления:
умения анализировать, выделять главное,
сравнивать, обобщать и систематизировать,
развивать устную и письменную речи, внимание и
память; продолжить работу по развитию умения
самостоятельно приобретать новые знания;
использование для достижения поставленной
задачи уже полученных знаний.
3. Воспитывающая: содействовать
воспитанию интереса к математике, активности,
дисциплинированности, честности,
ответственности за свой труд и труд
одноклассника, воспитание навыков самоконтроля
и взаимоконтроля.
Оборудование:
- линейка, карандаш, треугольник;
- компьютер, мультимедийный проектор,
интерактивная доска; - презентация.
Литература
- Учебник Геометрия 7-9 классы: учеб. для
общеобразоват. учреждений Л.С. Атанасян, В.Ф.
Бутузов. - Уроки геометрии с применением информационных
технологий. 7-9 классы. Методическое пособие с
электронным приложением, / Е.М.Савченко. – 2-е
издание, стереотипное. Москва “Планета”, 2012.
Ход урока
I. Организационный момент
ІI. Активизация познавательной деятельности
- Один из учащихся доказывает теорему о сумме
углов треугольника. - Второй учащийся решает на доске задачу № 230.
- Устно со всем классом решаем задачи по готовым
чертежам.
Вычислить все неизвестные углы треугольника
- Найдите неизвестный угол треугольника, если у
него два угла равны 50° и 60°. (Слайд 2, рисунок 1). Презентация - Найдите неизвестный угол треугольника, если у
него один угол прямой, а другой равен 20°. (Слайд 2,
рисунок 2) - Найдите угол при основании равнобедренного
треугольника, если угол между боковыми сторонами
40°. (Слайд 2, рисунок 3) - Найдите угол между боковыми сторонами
равнобедренного треугольника, если угол при
основании у него равен 30°. (Слайд 2, рисунок 4) - Вычислить все неизвестные углы прямоугольного
равнобедренного треугольника. (Слайд 3, рисунок 1) - Вычислить все неизвестные углы равностороннего
треугольника. (Слайд 3, рисунок 2) - Вычислите все неизвестные углы треугольников
(Слайд 4) - Определите вид треугольника (Слайды 5, 6, 7)
III. Изучение нового материала.
Вступительное слово учителя (постановка
проблемы урока).
Ребята, сегодня перед нами стоит такая
проблема: нам нужно познакомиться ещё с одним
углом, с которым мы раньше не встречались, у
которого так же есть своё свойство. Мы сегодня
повторили многие углы, которые мы знаем, и
некоторые из них помогут нам в решении нашей
поставленной задачи.
1. Ввести понятие внешнего угла треугольника:
Ребята, давайте выполним следующую
практическую работу, а именно:
- Постройте произвольный треугольник АВС
- Проведите луч ВД так, чтобы полученный угол
был смежным с углом В треугольника АВС.
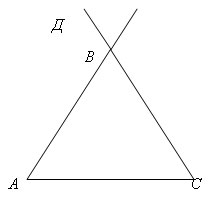
варианта АВД
или СВД)
внутри или вне его?
называются внешними углами треугольника.
треугольника и его свойство”
этого треугольника построить внешние углы?
внешнего угла треугольника.
Вывод: Внешним углом треугольника называется
угол, смежный с каким-нибудь углом этого
треугольника.
IV. Физкультминутка.
а) Дыхательное упражнение.
б) Упражнение для позвоночника.
в) Упражнение для глаз.
Вывод: Внешний угол треугольника равен сумме
двух других углов треугольника, не смежных с ним.
Это и есть свойство внешнего угла треугольника,
и мы его вместе доказали.
V. Решение задач
1. Устно решить задачу: в треугольнике АВС =110°.
Чему равны:
а) сумма остальных внутренних углов
треугольника?
б) внешний угол при вершине С?
2. По готовому чертежу на доске устно решить
задачу:
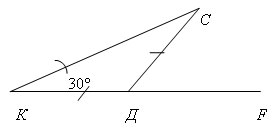
Найдите внутренние и внешний угол СДF
треугольника КСД.
3. Решить задачу № 232 под руководством учителя
на доске и в тетрадях.
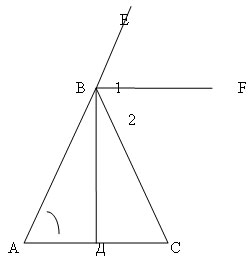
Дано: внешний угол треугольника АВС; .
Доказать: равнобедренный.
Решение
Проведем биссектрисы ВF и ВД смежных
углов СВЕ и АВС, тогда ВF || АС, так как , а углы 1 и А
соответственные при пересечении прямых ВF и АС секущей
АВ, ВД , так
как ВД , а
BF || AC.
В треугольнике АВС биссектриса ВД
является высотой, следовательно, треугольник АВС
– равнобедренный (см. задачу № 133)
2. Обратное утверждение также верно, а именно:
если треугольник равнобедренный, то внешний угол
при вершине, противолежащей основанию
треугольника, в два раза больше угла при
основанию Действительно, этот внешний угол равен
сумме двух углов при основании равнобедренного
треугольника, с так как углы при основании равны,
то данный внешний угол в два раза больше угла при
основании треугольника.
VI. Самостоятельная работа обучающего характера
(на четыре варианта)
Вариант 1
1. Один из углов равнобедренного треугольника
равен 96°. Найдите два других угла.
2. В треугольнике СДЕ с углом проведена биссектриса СF, . Найдите
Вариант 2
1. Один из углов равнобедренного треугольника
равен 108°. Найдите два других угла.
2. В треугольнике СДЕ проведена биссектриса СF,
,.
Найдите
Вариант 3
1. В равнобедренном треугольнике МNP c
основанием MP и углом проведена высота MH. Найдите .
2. В треугольнике СДЕ проведены биссектрисы СК
и ДР, пересекающиеся в точке F, причем Найдите
Вариант 4
1. В равнобедренном треугольнике СДЕ c
основанием СЕ и углом проведена высота СH. Найдите .
2. В треугольнике АВС проведены биссектрисы АМ
и BN, пересекающиеся в точке K, причем Найдите
VII. Домашнее задание: изучить пункты 30-31;
ответить на вопросы 1-5 на стр. 84; решить задачи №
233, 235.
VIII. Итоги урока
С чем мы сегодня познакомились?
– Что такое внешний угол треугольника?
– Какое свойство внешнего угла мы сегодня
доказали?
– Чему вы сегодня научились?
– Какие теоремы сегодня на уроке мы
использовали при решении задач?
IX. Рефлексия
Источник
Определение. Треугольник – фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами.
Типы треугольников
По величине углов

Остроугольный треугольник – все углы треугольника острые.

Тупоугольный треугольник – один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник – один из углов треугольника прямой (равен 90°).
По числу равных сторон

Разносторонний треугольник – все три стороны не равны.

Равнобедренный треугольник – две стороны равны.

Равносторонним треугольник или правильный треугольник – все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 – 2bc·cos α
b2 = a2 + c2 – 2ac·cos β
c2 = a2 + b2 – 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 23√2(mb2 + mc2) – ma2
b = 23√2(ma2 + mc2) – mb2
c = 23√2(ma2 + mb2) – mc2
Медианы треугольника

Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, – центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc’ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p – a)b + c
lb = 2√acp(p – b)a + c
lc = 2√abp(p – c)a + b
где p = a + b + c2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться
- внутри треугольника – для остроугольного треугольника;
- совпадать с его стороной – для катета прямоугольного треугольника;
- проходить вне треугольника – для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc =
1a
:
1b
:
1c
= (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:
ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:
Окружность вписанная в треугольник

Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру:
r = Sp
Радиус вписанной в треугольник окружности через три стороны:
r = (a + b – c)(b + c – a)(c + a – b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:
1r = 1ha + 1hb + 1hc
Окружность описанная вокруг треугольника

Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь:
R = abc4S
Радиус описанной окружности через площадь и три угла:
R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):
R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.
d2 = R2 – 2Rr
= 4 sin
α2
sin
β2
sin
γ2
= cos α + cos β + cos γ – 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.

Средняя линия треугольника параллельна основанию и равна его половине.
MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника
S∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок – средняя линия.
Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS =
12
a · ha
S =12
b · hb
S =12
c · hc
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
где p =
a + b + c2
– полупериметр треугльника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S =
12
a · b · sin γ
S =12
b · c · sin α
S =12
a · c · sin β
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их
соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников

Определение. Подобные треугольники – треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK = k2
Источник
