Каким свойством обладают односторонние углы

Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.

Углы по определению

Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.

Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.

Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.

Доказательство теоремы

Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.

Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.

Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.

Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.

Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.

Следствие из свойства прямых

На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.

Далее можно провести через С1 линию с, перпендикулярную а.

Затем через точку А нужно начертить АС2, которая параллельна с.

После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.

Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.

Построение параллелограмма

Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.

Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.

Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:

По построению AB=BD=AD.

Следовательно, AB=CD.

Точки C и D равноудалены от A и B.

Отрезки AB и CD параллельны.

Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.

Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.

Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.

ГеометрияКак провести перпендикуляр к прямой – правило построения

ГеометрияПериметр равностороннего треугольника – формула и примеры нахождения

Источник

Внутренние односторонние углы

Углы по определению

Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.

Доказательство теоремы

Доказательство теоремы внутренних односторонних углов

Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.

Следствие из свойства прямых

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.
Далее можно провести через С1 линию с, перпендикулярную а.
Затем через точку А нужно начертить АС2, которая параллельна с.
После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.
Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.

Построение параллелограмма

По построению AB=BD=AD.
Следовательно, AB=CD.
Точки C и D равноудалены от A и B.
Отрезки AB и CD параллельны.
Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.

Источник

Что такое параллельные прямые

Определение

Параллельные прямые — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.

Основные признаки:

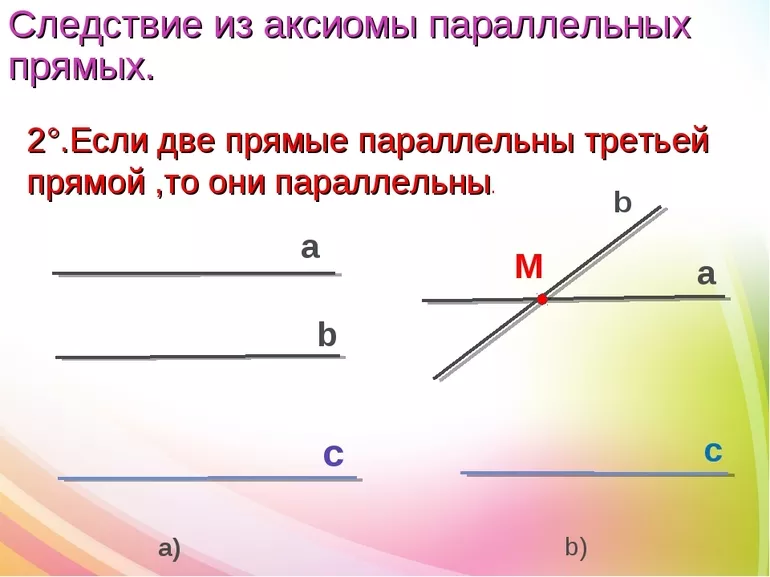
В случае, если две прямые параллельны третьей, они являются параллельными между собой. Так, если а || c и также b || c, то и a || b.
Если они перпендикулярны по отношению к третьей, то они не пересекаются: т.е., если а ⊥ с и b ⊥ c, то a || b.

Свойства параллельных прямых с доказательством

Определение

Свойства параллельных прямых — это утверждения, являющиеся обратными по отношению к признакам, упомянутым ранее.

Они обладают следующими свойствами:

Через любую точку, которая, что немаловажно, не лежит на прямой, можно провести параллель, притом лишь одну. Данное утверждение является Евклидовой аксиомой.
Если прямая, лежащая на плоскости, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой: если a || b и c ⊥ a, то c ⊥ b.

Дано: a || b и c ⊥ a

Доказать: c ⊥ b

Доказательство:

с пересекает а, следовательно, с пересекает также прямую, параллельную а, т.е. b.
Исходя из этого, можно утверждать, что с — это секущая по отношению к а и b.
При секущей с ∠1 и ∠2 являются накрест лежащими.
Из свойств углов при параллельных прямых, пересеченных секущей, нам известно о равенстве накрест лежащих углов: следовательно, ∠1 = ∠2.
Как следствие, ∠2 = 90 градусов, что означает, что c ⊥ b. Что и требовалось доказать.

Признаки при пересечении секущей

Определение

Секущей называется прямая, пересекающая:

кривую в двух точках;
или две прямые, которые лежат в этой же плоскости, в двух разных точках.

Рассмотрим признаки, которые характерны для параллельных прямых при пересечении их секущей.

Если соответственные углы равны, то прямые не пересекаются. Если ∠2 = ∠4, следовательно, a || b.

Если сумма внутренних односторонних углов равняется 180 градусам, то прямые являются параллельными. Если ∠1 + ∠2 = 180°, следовательно, a || b.

Если внутренние накрест лежащие углы равны, то прямые также являются параллельными. Если ∠1 = ∠3, следовательно, a || b.

Свойства углов при параллельных прямых и секущей

Кроме того, следует охарактеризовать основные свойства углов, образованных при пересечении секущей прямой. Данные свойства являются обратными рассмотренным выше признакам.

При пересечении двух параллельных прямых третьей, сумма внутренних односторонних углов, образованных ими, равняется 180 градусам: если a || b, то ∠1 + ∠2 = 180°.

В случае, когда две параллельные прямые пересечены третьей, соответственные углы, образованные ими, равны: если a || b, то ∠2 = ∠4.

Если две параллельные прямые пересекаются третьей, накрест лежащие углы, образованные ими, равны: если a || b, то ∠1 = ∠3.

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Ёжику Понятно

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол AOB

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.

Величину угла измеряют в градусах. ∠AOB=24°.

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180°.

Пример:

Пары углов

(1) и (3)
(2) и (4)

называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB
∠BOD=∠AOC

Пары углов

(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)

называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

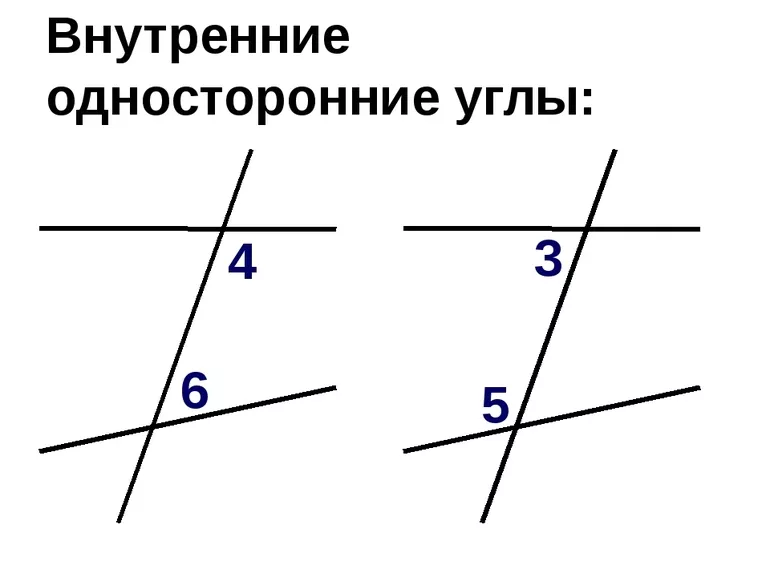
Пары углов:

(3) и (5)
(4) и (6)

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:

(1) и (7)
(2) и (8)

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

(3) и (6)
(4) и (5)

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

(1) и (8)
(2) и (7)

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

Соответственные углы равны.
Внутренние накрест лежащие углы равны.
Внешние накрест лежащие углы равны.
Сумма внутренних односторонних углов равна 180°.
Сумма внешних односторонних углов равна 180°.

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: S3=180°⋅(3−2)=180°

Сумма углов четырехугольника: S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n

Модуль геометрия: задания, связанные с углами

Скачать домашнее задание к уроку 2.

Источник

Что такое параллельные прямые в пространстве

Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться. Мы рассмотрим первое свойство.

Впервые теорию о параллельности научно обосновал греческий ученый Евклид в своей работе под названием «Начала».

Определение

Параллельные прямые в пространстве — прямые, лежащие в одной плоскости и не имеющие пересечений друг с другом.

Обозначение параллельных прямых

Сами прямые обозначаются латинскими буквами. Например, l и k. Параллельность обозначается символом: ||

Теорема о параллельных прямых, формулировка

Теорема

Если любая точка в пространстве не расположена на рассматриваемой прямой, то через нее проводима лишь одна прямая, которая будет параллельна рассматриваемой.

Доказательства закона представим в заключительном разделе статьи.

Типы углов при параллельных прямых

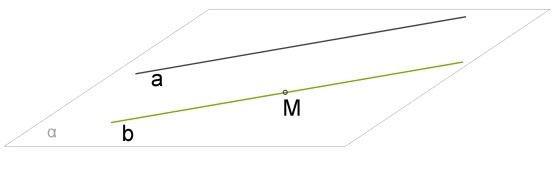
Когда прямая пересекает две другие параллельные друг другу прямые, образуется восемь углов. В геометрии они имеют свои названия и свойства. Для дальнейшего разбора темы этой статьи достаточно разобраться в трех видах. Далее при рассмотрении каждого вида в отдельности ориентируйтесь на рисунок ниже:

Односторонние

На рисунке выше это ∠1 и ∠6, а также ∠4 и ∠7. Они расположены с одной стороны относительно прямых.

Соответственные

Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8. Их расположения отличается тем, что они как бы разделены между собой одной из прямых.

Накрест лежащие

На данном рисунке это ∠3 и ∠5, ∠2 и ∠8, ∠1 и ∠7, ∠4 и ∠6. Их расположение легко запомнить, так как они размещаются по принципу «крест-накрест».

Условия параллельности

Чтобы доказать параллельность прямых, нужно знать признаки, по которым она определяется. Достаточно соблюдения хотя бы одного из нижеследующих условий.

Накрест лежащие углы равны

Дано: (a;vertvert b), AB является секущей, углы 1 и 2 — накрест лежащими.

Доказать: равенство ∠1 и ∠2.

Доказательство: допустим, что ∠1 и ∠2 не равные. Тогда проведем угол PAB, причем он будет накрестлежащим с ∠2.

Накрест лежащие углы равны. Из этого следует, что AP (vertvert) b. Но это невозможно, потому что через точку a может проходить только одна прямая, согласно аксиоме, а у нас получилось две — b и A. Поэтому наше предположение неправильное и ∠1=∠2. Ч.т.д.

Соответственные углы равны

∠1 и ∠2 являются соответственными.

Задача

MN (vertvert) AD. Доказать, что( angle NMC=angle BAD).

Решение: (angle NMC=angle DAC) (как соотв.), а (angle DAC=angle BAD) (AD — биссектриса). Следовательно, (angle NMC=angle BAD).

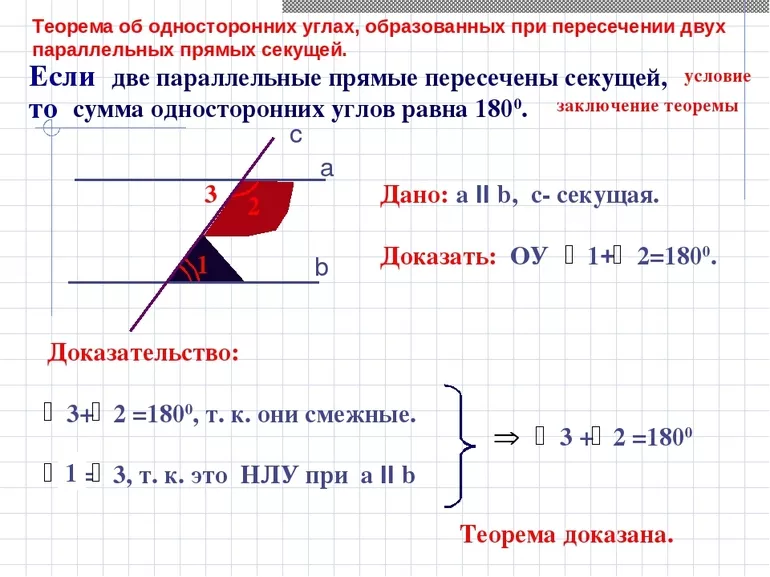
Сумма односторонних углов равна 180 градусов

Сумма ∠1 и ∠2 равна 180º

Доказательство:

a (vertvert) b, поэтому ∠1=∠3 (соотв.). ∠2+∠3=180º (смеж.). Поэтому при сложении получаем 180º.

Если обе прямые параллельны третьей

Этот признак называют также теоремой о трех параллельных прямых на плоскости. Если a (vertvert) b и c (vertvert) b, то a (vertvert) c.

Доказательство

Есть a (vertvert) b. Допустим, что существует еще c (vertvert) a. Согласно условию, a не пересекает b и наоборот.

В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом

Здесь то же самое, что в предыдущем пункте: в случае, когда a и c ||, а b и c также ||, то a и b тоже ||.

Две прямые, перпендикулярные третьей, параллельны

Обозначение перпендикулярных прямых: ⊥

На картинке видно, что a (perp) c и b (perp) c. Отсюда, согласно этому признаку-теореме, следует, что a (vertvert) b.

Доказательство

Допустим, что a (perp) c и b (perp) c, но a не (vertvert;)b. Тогда a и b пересекаются в какой-то точке. Рассмотрим треугольник ABC. Сумма его углов будет равна 180º+∠C. Но так быть не может. Значит, наше предположение неверно, и a (vertvert) b.

Доказательство параллельности прямых

Ниже представлено доказательство теоремы из первого раздела статьи.

Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа ((alpha)). Известно, она единственная.Прямая b проходит через т.М и (vertvert;) а. Она существует, что доказывает аксиома о (;vertvert.)
Предположим, что существует прямая с, которая тоже проходит через т.М, причем c (vertvert) a. В этом случае потребуется другая плоскость (beta), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость ((alpha) совпала с (beta)) и одна и та же прямая (b совпал с c). Единственность прямой доказана.

Теорема доказана.

Уравнение параллельной прямой

Если известно, что прямая проходит через какую-то точку с координатами и параллельна другой прямой y=kx+a, то ее уравнение можно найти по формуле:

(gamma-gamma_0=kappaleft(chi-chi_0right))

где k — угловой коэффициент.

Источник