Каким свойством обладают точки

- Главная
- Вопросы & Ответы
- Вопрос 12859546
Васян Коваль
более месяца назад
Просмотров : 21
Ответов : 1
Лучший ответ:
Таня Масян
1)все точки окружности находятся на одинаковом расстояние от центра.
2)расстояние от центра до любой точки вне этой окружности больше радиуса.
Радиус-отрезок соединяющий центр окружности с любой точки, лежащей на этой окружности.
диаметр-отрезок, соединяющий две точки окружности и проходящий через центр окружности.
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Таня Масян
Два поезда одновременно отошли в противоположных направлениях. Их скорости 60 км/ч и 70 км/ч
более месяца назад
Смотреть ответ
Просмотров : 5
Ответов : 1
Энджелл
образование в природе у озона
более месяца назад
Смотреть ответ
Просмотров : 4
Ответов : 1
Пармезан Черница
В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведения получившихся чисел оказалась равным 2007.Какая отметка выходит у Вовочки в четверти по пению?(“Колов” учительница пения не ставит) умоляю такое решить сложн…
более месяца назад
Смотреть ответ
Просмотров : 4
Ответов :
Главный Попко
помогите пж пж помогите пж
более месяца назад
Смотреть ответ
Просмотров : 6
Ответов : 1
Картинок: 1
Васян Коваль
Детскую библиотеку за 4 дня посетили 423 человека.В 1день её посетили 43 человека.Во второй день -в 2 раза больше,чем в первый,но на 117 человек меньше,чем в третий день.Сколько человек посетили библиотеку в четвёриый день?
более месяца назад
Смотреть ответ
Просмотров : 7
Ответов : 1
Источник
ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 1811
Назад к содержанию
Условие
Каким свойством обладают точки окружности? Какой отрезок называют радиусом окружности? Диаметром окружности? Начертите окружность и проведите три радиуса этой окружности и её диаметр.
Решение 1
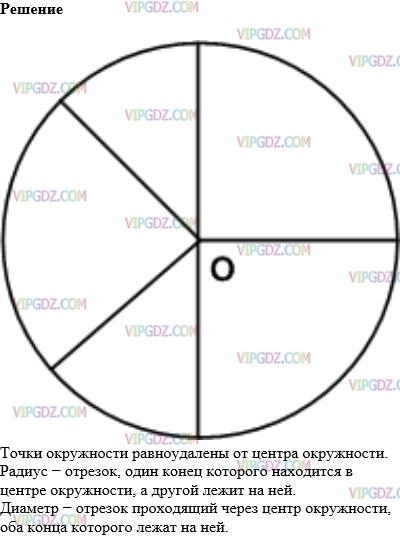
Решение 2

Решение 3

Другие задачи из этого учебника
- 1808
- 1809
- 1810
- 1811
- 1812
- 1813
- 1814
Поиск в решебнике
Популярные решебники
ГДЗ по Математике за 5 класс: Виленкин Н.Я
Издатель: Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. 2013г.
ГДЗ по Математике за 5 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.
ГДЗ по Математике за 5 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.
ГДЗ по Математике за 5 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017г.
ГДЗ по Математике за 5 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2013г.
Источник
Этой статьей начинаем с Вами изучение одного из самых сложных и запутанных, но одновременно прекрасных, выверенных, наглядных и точных направлений математики – общей топологии. Название – не игра слов, к концу этой заметки Вы поймете, как математика относится ко всему роду homo sapiens. Начинаем!
Это так называемая бутылка Клейна – не правда ли завораживает? Какими свойствами обладает это фигура, можно ли ее построить в нашем трехмерном мире, как пройти из одной точки бутылки Клейна в другую?
Тополо́гия (от др. греч τόπος — место и λόγος — слово, учение) – наука, изучающая качественные свойства фигур не только в привычном нам трехмерном мире, но и в мирах с большим и меньшим количеством измерений (уж поверьте все вы сталкивались с ними, только может быть не догадывались).
Самый простой пример пространства меньшей размерности – это плоскость у которой размерность равна 2, подобно тому, как у прямоугольника есть ширина и длина.
Проделаем такой эксперимент: возьмем на плоскости квадрат и начнем его сжимать по краям, как бы сглаживая углы. После некоторого количества движений и выравниваний мы сможем получить круг – другую геометрическую фигуру. Процесс обратим – из этого круга мы всё так же можем получить квадрат. Значит ли это, что квадрат равен кругу, а круг квадрату? Конечно нет, но обычный человек сказал бы: “Они подобны”, а тополог скажет: “Они гомеоморфны или получены гомеоморфным преобразованием”.
Стрелки – направление растягивания.
Страшное слово? Как бы не так! Каждый из Вас (во всяком случае женская половина моей аудитории)за свою жизнь проводил гомеоморфные преобразования: “отщипнул тесто – сделал из него шар – раскатал в блин”.
Гомеоморфное преобразование – это ни что иное, как растягивание или сжатие точек какой-либо фигуры без образования разрывов и склеек одинаковых точек. Возьмите раскатанный блин и порвите его по центру – получите негомеоморфное преообразование.
Возникает резонный вопрос, а какие свойства остаются неизменными при гомеоморфизме? Математики называют такие свойства качественными или топологическими и если мы хотим говорить о них, то должны как-то охарактеризовать эти свойства, хотя бы интуитивно-наглядно. Очередной эксперимент:
Возьмем сферу – поверхность точек, равноудаленную от другой точки, называемой центром сферы. Сфера – пуста, если наполнить сферу любым веществом (в нашем случае мягким и эластичным) получится шар. Попытаемся понять, чем “топологически” отличается сфера от шара?
1) Зададимся вопросом: как наикратчайшим образом добраться из одной точки сферы в другую, противоположную ей (например. с северного на южный полюс)? Правильно, пойти как нормальный человек по поверхности. А для шара? Теоретически мы могли бы “срезать” добрую часть путь проникнув через его центр и прошив его насквозь. Есть отличие!
Напоминаю, что по “пустоте” мы не перемещаемся, а внутри шара – пустота.
2) Представьте, что вы решили прокатить по поверхности сферы колесо и вернуться в ту же точку. Изменится ли направление его вращения после Вашего с ним кругосветного приключения? Очевидно и для сферы и для шара, что нет.
Именно поэтому у кругосветных путешественников-автомобилистов колеса по приезду в родной город не крутятся в одну сторону
Но есть фигуры, прокатив колесо по которым и вернувшись в ту же точку мы изменим направление его вращения! Пример – широко известный лист Мёбиуса.
Источник: https://ds04.infourok.ru/uploads/ex/01a0/001892af-c470c37a/1/hello_html_m1ce4bf27.jpg
Это свойство фигур называется ориентируемость. Шар и сфера – ориентируем, а вот лист Мёбиуса – нет. Здесь отличий между шаром и сферой не выявлено.
3) Из определения следует, что под поверхностью сферы пустота. В шаре такого нет, он заполнен полностью.
Именно в третьем различии вся “соль”. Что же из него следует?
Представьте, что Вы взяли комок мокрого снега и хотите придать ему идеальную форму.
Снег еще рыхлый, поэтому сжимая снег со всех сторон Вы начнете “стягивать” точки этого шара к одной из его точек – центру.
А теперь попробуйте стянуть футбольный мяч хотя бы к одной его точке. Попробуем стянуть северный (N) и южный полюса (S). Суть в том, что в предельном приближении мяч порвется в точках W и E, а разрыв, как мы помним из определения, недопустим при гомеоморфизме.
Таким образом, мы не смогли гомеоморфно стянуть сферу к какой-либо из своих точек (зато сферу мы можем вывернуть наизнанку – видео в конце статьи), а шар смогли. В этом и заключается топологическое различие между этими фигурами: шар не гомеоморфен сфере. Остается открытым вопрос: чему же тогда гомеоморфен шар и сфера? Ответ: кубу.
Источник: https://ruread.net/bookimages/45203/img_41.jpg
Со сферой всё намного интереснее. Топологи различают сферу без ручки (тогда это просто сфера) и сферу с n-ручками, где n=1,2… Например, сфера с ручкой получается с помощью гомеоморфных преобразований из тора (бублика).
Так выглядит ручка – как подрезанный бублик.
Источник: https://habr.habrastorage.org/post_images/539/bb8/785/539bb878571fb370ff85bc9c70f4e8af.gif
Что же общего у кружки и тора? Ответ: количество дырок, и это ключевое топологическое свойство фигур. Фигуры с разным количеством дырок не могу быть гомеоморфны другу другу, не могут быть получены друг из друга посредством сжатия/растягивания. И это главный вывод нашего вводного экскурса. Где-то мог ошибиться, я думаю, найдутся корифеи. которые исправят в комментариях.
Стой, стой, а что же с человеком, который – шар с ручками?
Ах да, знакомьтесь – это человек-Шар и он попал в передрягу: у него руки закреплены между собой как два кольца.
Ему нужно помочь распутать руки не разрывая пальцы. Вы скажете невозможно, топологи скажут: элементарно.
Обещанное видео про выворачивание сферы наизнанку (завораживает):
Часть 1
Часть 2
Подведем итог:
1) Топология изучает качественные свойства геометрических фигур.
2) Топология не нарушается при гомеоморфном преобразовании: сжатии, растягивании или склейке.
3) Важнейшим топологическим свойством фигур является количество дырок.
4) Фигуры с разным количеством дырок не гомеоморфны.
На этом ознакомительная статья подходит к концу, но приступать к изучению топологии не на интуитивно-бытовом уровне еще рано. Необходимо дать и другие основополагающие понятия. а именно множества и расстояния. Этим категориям и будут посвящены следующие статьи этого цикла.
ПРОДОЛЖЕНИЕ (МОЖЕТ, НУДНОЕ, НО НУЖНОЕ)
Часть 2. Определения множества и подмножества.
Часть 3. Бинарные операции над множествами.
Часть 4. Унарные операции над множествами
Часть 5. Законы де Моргана и диаграммы Эйлера-Венна (выйдет вечером 24.05) – подпишитесь на телеграмм-канал, чтобы не пропустить.
************************************************************************
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.
**************************************************************************
О чем я еще пишу:
Теорема неслучайности: неравенство Чебышева
Про факториал
Ответ тем, кто отрицает пользу математики в обычной жизни
Правда интересные числа, “мамой клянусь”
Экзотические тригонометрические формулы, которые не дают в школе
Источник
