Каким свойством обладают точки окружности что называют радиусом окружности

ГДЗ по классам
2 класс
- Математика
3 класс
- Математика
4 класс
- Математика
5 класс
- Математика
- Русский язык
- Английский язык
6 класс
- Математика
- Русский язык
- Английский язык
7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
10 класс
- Геометрия
- Химия
11 класс
- Геометрия
ГДЗ и решебники
вип уровня
- 2 класс
- Математика
- 3 класс
- Математика
- 4 класс
- Математика
- 5 класс
- Математика
- Русский язык
- Английский язык
- 6 класс
- Математика
- Русский язык
- Английский язык
- 7 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- 8 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 9 класс
- Русский язык
- Английский язык
- Алгебра
- Геометрия
- Физика
- Химия
- 10 класс
- Геометрия
- Химия
- 11 класс
- Геометрия
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 1811

Назад к содержанию
Условие
Каким свойством обладают точки окружности? Какой отрезок называют радиусом окружности? Диаметром окружности? Начертите окружность и проведите три радиуса этой окружности и её диаметр.
Решение 1
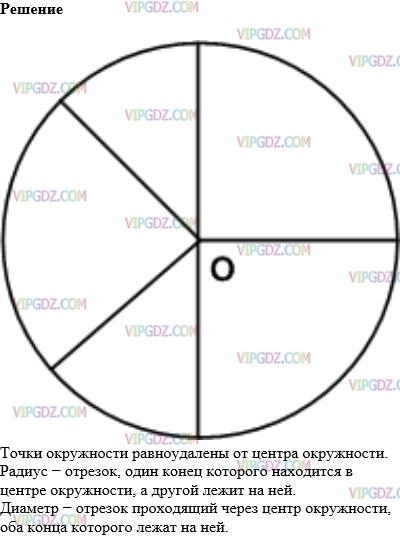
Решение 2

Решение 3

Другие задачи из этого учебника
- 1808
- 1809
- 1810
- 1811
- 1812
- 1813
- 1814
Поиск в решебнике
Популярные решебники
 ГДЗ по Математике за 5 класс: Виленкин Н.Я
ГДЗ по Математике за 5 класс: Виленкин Н.Я
Издатель: Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. 2013г.
 ГДЗ по Математике за 5 класс: Мерзляк А.Г.
ГДЗ по Математике за 5 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.
 ГДЗ по Математике за 5 класс: Никольский С.М.
ГДЗ по Математике за 5 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.
 ГДЗ по Математике за 5 класс: Дорофеев Г.В.
ГДЗ по Математике за 5 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017г.
 ГДЗ по Математике за 5 класс: Зубарева, Мордкович
ГДЗ по Математике за 5 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2013г.
Источник
- Главная
- Вопросы & Ответы
- Вопрос 12859546

Васян Коваль
более месяца назад
Просмотров : 16
Ответов : 1
Лучший ответ:


Таня Масян
1)все точки окружности находятся на одинаковом расстояние от центра.
2)расстояние от центра до любой точки вне этой окружности больше радиуса.
Радиус-отрезок соединяющий центр окружности с любой точки, лежащей на этой окружности.
диаметр-отрезок, соединяющий две точки окружности и проходящий через центр окружности.
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:

Таня Масян
Два поезда одновременно отошли в противоположных направлениях. Их скорости 60 км/ч и 70 км/ч
более месяца назад
Смотреть ответ
Просмотров : 3
Ответов : 1

Энджелл
образование в природе у озона
более месяца назад
Смотреть ответ
Просмотров : 3
Ответов : 1

Пармезан Черница
В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведения получившихся чисел оказалась равным 2007.Какая отметка выходит у Вовочки в четверти по пению?(“Колов” учительница пения не ставит) умоляю такое решить сложн…
более месяца назад
Смотреть ответ
Просмотров : 2
Ответов :

Главный Попко
помогите пж пж помогите пж
более месяца назад
Смотреть ответ
Просмотров : 4
Ответов : 1
Картинок: 1

Васян Коваль
Детскую библиотеку за 4 дня посетили 423 человека.В 1день её посетили 43 человека.Во второй день -в 2 раза больше,чем в первый,но на 117 человек меньше,чем в третий день.Сколько человек посетили библиотеку в четвёриый день?
более месяца назад
Смотреть ответ
Просмотров : 6
Ответов : 1
Источник
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
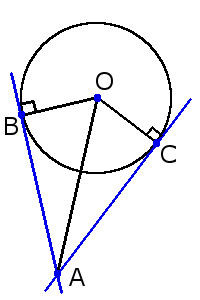
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
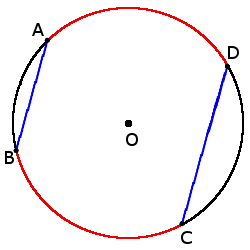
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
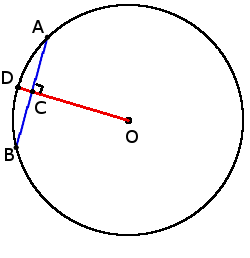
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
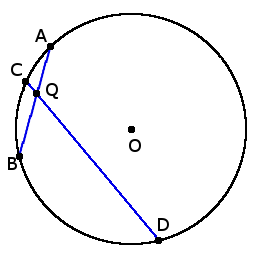
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
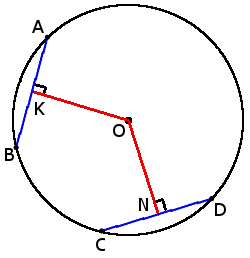
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
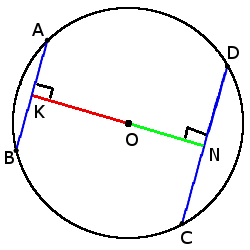
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
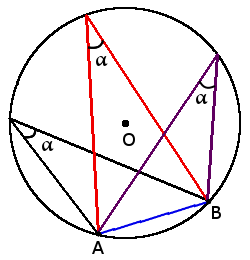
1. Все вписанные углы, которые опираются на одну дугу – равны.
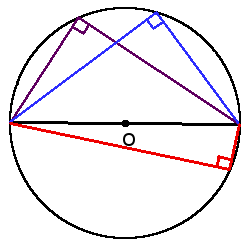
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
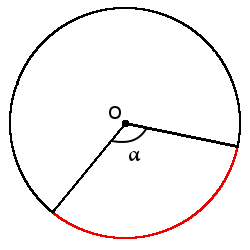
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
Окружность (C), её центр (O), радиус (R) и диаметр (D)
Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.
Построение окружности циркулем
Практическое построение окружности возможно с помощью циркуля.
Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква обозначает радиус окружности.
Хорды, дуги и касательные[править | править код]
Секторы круга
Прямая может иметь с окружностью не более двух общих точек.
Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды[3].
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности[5].
Углы[править | править код]
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Говорят, что центральный или вписанный углы опираются на дугу, высекаемую на окружности их лучами, или же на хорду, стягивающую эту дугу.
Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.
Из определения радиана следует, что длина любой дуги окружности связана с центральным углом , опирающимся на эту дугу, простым соотношением[6]: (при этом длина хорды, стягивающей ту же дугу, равна ). Поскольку длина окружности равна , с ростом угла значение его радианной меры меняется от 0 до
Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.
Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.
Свойства вписанных углов:
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
- Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Другие свойства:
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
- Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.
Свойства[править | править код]
Формулы[править | править код]
Если радиус круга равен 1, то его окружность равна 2π.
Длина окружности:
Радиус окружности:
Диаметр окружности:
Площадь круга радиуса R:
Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:
Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:
История[править | править код]
Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.
Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.
Окружность получается как сечение конуса плоскостью, перпендикулярной его оси
Аналитическая геометрия окружностей[править | править код]
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.
Декартовы координаты[править | править код]
Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)
Общее уравнение окружности записывается как:
или
где
Точка — центр окружности, — её радиус.
Уравнение окружности радиуса с центром в начале координат:
Уравнение окружности, проходящей через точки не лежащие на одной прямой (с помощью определителя):
Тогда в явном виде координаты центра окружности определяются по формулам:
Окружность также можно описать с помощью параметрического уравнения:
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
Если центр окружности совпадает с началом координат, функции принимают вид:
Полярные координаты[править | править код]
Окружность радиуса с центром в точке :
Если полярные координаты центра окружности то проходящая через начало координат окружность описывается уравнением:
Если же центр является началом координат, то уравнение будет иметь вид
Комплексная плоскость[править | править код]
На комплексной плоскости окружность задаётся формулой:
или в параметрическом виде
Окружности в пространстве[править | править код]
В пространстве окружность радиуса с центром в точке можно определить как контур диаметрального сечения сферы
плоскостью
,
где — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы
Например, при решения этой системы можно задать параметрически следующим образом:
Касательные и нормали[править | править код]
Уравнение касательной к окружности в точке определяется уравнением
Уравнение нормали в той же точке можно записать как
Концентрические и ортогональные окружности[править | править код]
Концентрические окружности
Окружности с общим центром, но разными радиусами, называются концентрическими. Две окружности, заданные уравнениями:
являются концентрическими в том и только в том случае, когда и
Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие
Дополнительные сведения[править | править код]
Определение треугольников для одной окружности[править | править код]
- Треугольник ABC называется вп

