Какими свойствами не обладает вектор
Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
Определение 8
Суммой векторов $overline{a+b}$ будем называть вектор $overline{c}=overline{AC}$, который построен следующим образом: От произвольной точки A отложем $overline{AB}=overline{a}$, далее от точки $B$ отложем $overline{BC}=overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Определение 9
Произведением вектора $overline{a}$ на $k∈R$ будем называть вектор $overline{b}$ который будет удовлетворять условиям:
- $|overline{b}|=|k||overline{a}|$;
- $overline{a}↑↑overline{b}$ при $k≥0$ и, $overline{a}↑↓overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$:
Коммутативность сложения векторов:
$overline{α}+overline{β}=overline{β}+overline{α}$
Ассоциативность трех векторов по сложению:
$(overline{α}+overline{β})+overline{γ}=overline{α}+(overline{β}+overline{γ})$
Сложение с нулевым вектором:
$overline{α}+overline{0}=overline{α}$
Сложение противоположных векторов
$overline{α}+(overline{-α})=overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $overline{α}$, $overline{β}$ и чисел $a$ и $b$.
- $a(overline{α}+overline{β})=aoverline{α}+aoverline{β}$
- $overline{α}(a+b)=overline{α}a+overline{α}b$
- $(ab)overline{α}=a(boverline{α})=b(aoverline{α})$
- $1cdot overline{α}=overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Пример 1
Провести сложение векторов
$2overline{AB}+(2overline{BC}+3overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2overline{AB}+(2overline{BC}+3overline{AC})=(2overline{AB}+2overline{BC})+3overline{AC}$
Используя свойство умножения на число 1, получим:
$(2overline{AB}+2overline{BC})+3overline{AC}=2(overline{AB}+overline{BC})+3overline{AC}=2overline{BC}+3overline{AC}=5overline{AC}$
Ответ: $5overline{AC}$.
Источник
Содержание:
- Действия над векторами
- Свойства операции сложения:
- Свойства умножения вектора на число:
- Свойства скалярного произведения:
- Свойства векторного произведения:
- Свойства смешанного произведения:
В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.
Действия над векторами
Определение
Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ – начало, точка
$B$ – конец вектора.
Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец – с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.
Свойства операции сложения:
1 $overline{a}+overline{b}=overline{b}+overline{a}$ – коммутативность
2 $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ – ассоциативность
3 $overline{a}+overline{0}=overline{a}$
4 $overline{a}+(-overline{a})=overline{0}$
Определение
Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.
Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:
- $overline{b} | overline{a}$
- $|overline{b}|=|alpha||overline{a}|$
- $overline{a} uparrow uparrow overline{b}$, если
$alpha>0$,
$overline{a} uparrow downarrow overline{b}$, если
$alpha lt 0$.
Свойства умножения вектора на число:
1 $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$
2 $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$
3 $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$
4 $1 cdot overline{a}=overline{a}$
5 $-1 cdot overline{a}=-overline{a}$
6 $0 cdot overline{a}=overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:
$$bar{a} bar{b}=bar{a} cdot bar{b}=(bar{a}, bar{b})=|bar{a}||bar{b}| cos (bar{a}, bar{b})$$
Свойства скалярного произведения:
1 $(overline{a}, overline{b})=(overline{b}, overline{a})$ – симметричность.
2 $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.
3 Если $overline{a} neq overline{0}$, то $(bar{a}, bar{b})=|bar{a}| cdot Пр_{bar{a}} bar{b}$
4 Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.
5 $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$
6 $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$
7 $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$
Определение
Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
$|bar{c}|=|bar{a}||bar{b}| sin (bar{a}, bar{b})$.
Свойства векторного произведения:
1 $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$
2 $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$
3 Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.
$$S=|[bar{a}, bar{b}]|=|bar{a}||bar{b}| sin (bar{a}, bar{b})$$
4 $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$
5 $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Свойства смешанного произведения:
1 $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2 $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3 Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4 Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c}) lt 0$, то векторы $overline{a}$, $overline{b}$ и $overline{c}$ образуют левую тройку векторов. lt /p> lt p>5 $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6 $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7 $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8 $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9 $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10 Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
Источник
Скалярные и векторные величины
Векторные величины – величины, для характеристики которых указывается как числовое значение, так и направление в пространстве. Например, сила, скорость, ускорение, напряженность поля (магнитного, электромагнитного) и т. п.
Скалярные величины – это величины, для характеристики которых достаточно только числовое значение в соответствующих единицах измерения. Например, масса, температура, длина, площадь, объём, количества тепла и т. д.
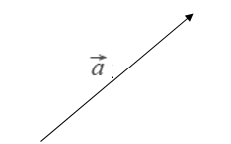
Рис. 1
Вектор – это геометрическое изображение векторной величины в заданном масштабе.
На рис. 1 А – начальная точка вектора, В – конец вектора. Вектор обычно обозначается стрелочками, которые ставят вверху букв, но многие люди для удобства ставят обычные чёрточки. Иногда вектор обозначают одной буквой: . Расстояние от точки к точке называют длиной или модулем вектора, а обозначается так: или
Если начало и конец вектора совпадают, тогда такой вектор называется нулевым и обозначается Направление нулевого вектора может быть произвольным.
Два ненулевых вектора, которые лежат на параллельных прямых или на одной прямой называются коллинеарными, а обозначаются
Нулевой вектор считается коллинеарным производного вектора.
Векторы, которые параллельны одной и той же плоскости, или те, которые лежат в одной плоскости, называются компланарными.
Равными называются векторы, если они удовлетворяют такие условия:
1) они коллинеарны;
2) их модули равны;
3) они направлены в одну сторону, то есть:
= = ,
Например, на рис. 2, где ABCD – параллелограмм,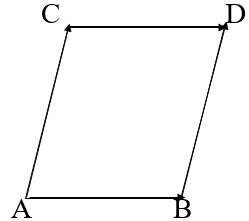
Рис. 2
где векторы = , = .
Если = , , тогда векторы и – противоположные.
Вектор противоположный вектору обозначают . Вектор противоположен вектору и записывается =
Из определения равенства векторов следует, что вектор можно переносить в пространстве параллельно самому себе, такие векторы называются свободными.
Вектор, модуль которого равен единице называется единичным, или ортом, и обозначается :
= ,
Линейные операции над векторами: сложение векторов, вычитание и умножение
Линейные операции над векторами или ещё говорят действия над векторами – это сложение векторов, вычитание и умножение вектора на число (скаляр).
Сложение векторов
Пусть заданы два вектора и . Отложим с некоторой точки вектор = , а тогда из точки отложим вектор = и рассмотрим вектор = .
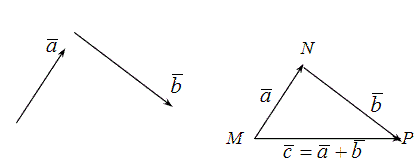
Рис. 3
Согласно рис. 3 вектор = и замыкает ломаную MNP, направление вектора берётся в конец последнего слагаемого .
По принципу замыкания находится сумма большего числа слагаемых.
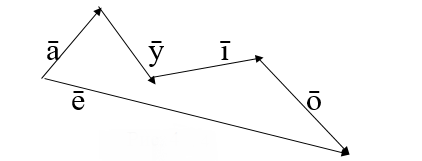
Рис. 4
Вычитание векторов
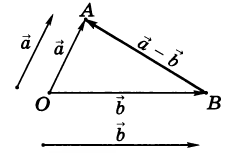
Рис. 5
Посмотрите на рис. 5. Мы поместили начало векторов и в одну точку , и построили замыкающий вектор .
Умножение вектора на число
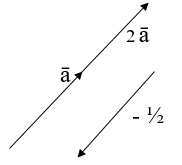
Направление вектора совпадает с направлением вектора , если , и противоположному направлению вектора , если .
При , или считается, что – нулевой вектор.
Рис. 6
Свойства векторов
Мы рассмотрели линейные операции над векторами и теперь можно рассмотреть свойства векторов, без которых невозможно решить многие задачи.
1).
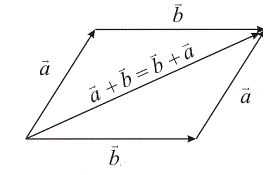
Рис. 7
Свойство 1 называется переставным или коммутативным, понятно с рис. 7, что разрешается прибавлять векторы по правилу параллелограмма.
2). – ассоциативное или соединительное свойство (см. рис. 8).
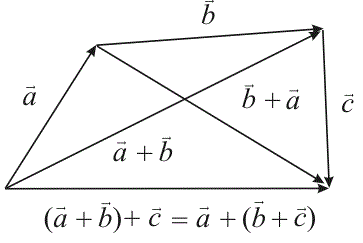
Рис. 8
3). .
4). .
5). x .
6). = .
7). x .
8). .
Свойства 3 – 8 вы уже сможете проверить самостоятельно.
Примеры
За данными вектора и построить векторы:
а) ,
б) .
Решение покажем на рисунке:
Первый рисунок решения a:
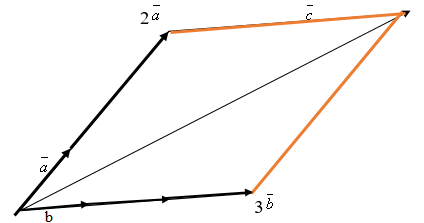
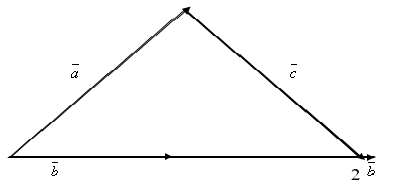
Второй рисунок решения б:
Источник
Прежде чем приступить к тематике статьи, напомним основные понятия.
Определение 1
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Определение 2
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Определение 3
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Определение 4
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Определение 5
Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
– для неколлинеарных векторов:
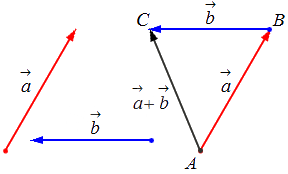
– для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
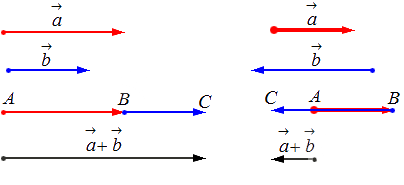
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Определение 6
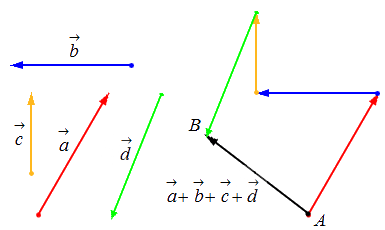
Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Определение 7
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и – b→.
Умножение вектора на число
Определение 8
Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
– еслиk>1, то это число приведет к растяжению вектора в k раз;
– если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
– если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
– если k=1, то вектор остается прежним;
– если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
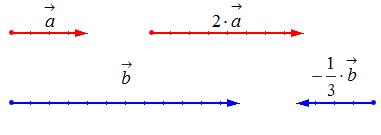
Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.
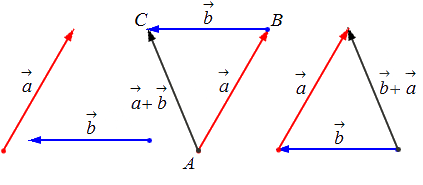
- Свойство коммутативности: a⇀+b→=b→+a→ .
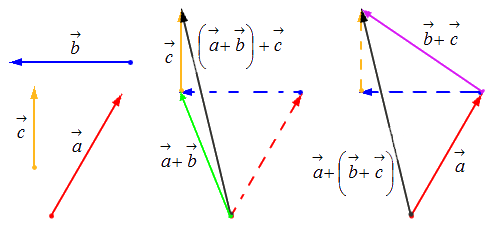
- Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство – очевидное.
- Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
- Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
Геометрически это свойство определяется подобием треугольников: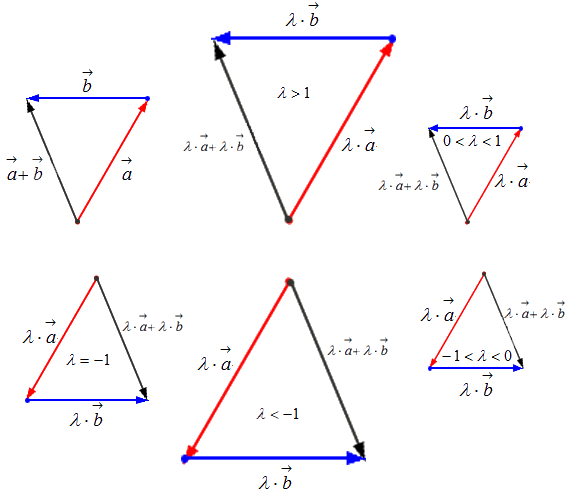
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Пример 1
Задача: упростить выражение a→-2·(b→+3·a→)
Решение
– используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
– задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
– используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
– затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→
Источник
ОПРЕДЕЛЕНИЕ
Вектор представляет собой направленный сегмент, который обозначается (
A B
) (начиная с точки (
A
), заканчивается в точке (
B
)) или (
overline{a}
)
Если концы вектора задаются по их координатам в пространстве (
A=left(a_{1}, a_{2}, a_{3}right)
), (
B=left(b_{1}, b_{2}, b_{3}right)
) , то координаты вектора
(
A B=left(b_{1}-a_{1}, b_{2}-a_{2}, b_{3}-a_{3}right)
)
ОПРЕДЕЛЕНИЕ
Модуль (длина) вектора (
overline{c}=left(c_{1}, c_{2}, c_{3}right)
) представляет собой число, равное расстоянию от начала до конца вектора, оно вычисляется по формуле:
(
overline{c}=sqrt{c_{1}^{2}+c_{2}^{2}+c_{3}^{2}}
)
Вектор называется одиночным, если его длина равна единице. Вектор называется нулевым, если его длина равна нулю.
Векторы (
overline{a}
) и
(
overline{b}
) называются коллинеарными, если они либо лежат на одной прямой, либо на параллельных прямых.
ОПРЕДЕЛЕНИЕ
Суммой векторов (
overline{a}
) и (
overline{b}
) (конец вектора (
overline{a}
) совпадает с началом (
overline{b}
) называется вектор (
overline{c}
) , начало которого совпадает с началом вектора (
overline{a}
), конец – с концом вектора (
b
).Графически это выглядит так, как показано на рисунке (правило треугольника)
Операция сложения векторов обладает такими свойствами
1.(
overline{a}+overline{b}=overline{b}+overline{a}
)
(
(overline{a}+overline{b})+overline{c}=a+(overline{b}+overline{c})
)
ОПРЕДЕЛЕНИЕ
Разностью векторов (
overline{a}
) и (
b
) называется такой вектор (
overline{c}
) , который в сумме с вектором (
overline{b}
) дает вектор (
overline{a}
).
Если векторы (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) заданы своими координатами, то сумма/разность этих векторов
(
overline{a} pm overline{b}=left(a_{1} pm b_{1}, a_{2} pm b_{2}, a_{3} pm b_{3}right)
)
ОПРЕДЕЛЕНИЕ
Произведением вектора (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) на число (
alpha
) называется вектор (
alpha cdot overline{a}=left(alpha a_{1}, alpha a_{2}, alpha a_{3}right)
) , который параллелен вектору (
overline{a}
) , сонаправлен (
overline{a}
) , если (
alpha>0
) , и противоположно направлен, если (
alphaОПРЕДЕЛЕНИЕ
Скалярным произведением векторов (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) называется число (
(overline{a}, overline{b})
), равное сумме произведений соответствующих координат:
(
(overline{a}, overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}
)
Также скалярное произведение векторов можно вычислить как произведение модулей векторов на косинус угла между ними:
(
(overline{a}, overline{b})=|overline{a}||overline{b}| cos (overline{a}, overline{b})
)
Свойства скалярного произведения
1.(
(overline{a}, overline{b})=(overline{b}, overline{a})
)
2.(
(overline{a}, overline{b}+overline{c})=(overline{a}, overline{b})+(overline{a}, overline{c})
)
3.(
(lambda overline{a}, overline{b})=(overline{a}, lambda overline{b})=lambda(overline{a}, overline{b})
)
4.(
(overline{a}, overline{a}) geq 0
)
5.(
(overline{a}, overline{a})=|overline{a}|^{2}
)
6.(
(overline{a}, overline{b})=0 Leftrightarrow overline{a} perp overline{b}
)
Векторным произведением векторов (
a
) и (
overline{b}
) называется вектор (
overline{c}=overline{a} times overline{b}
) (или (
overline{c}=[overline{a}, b]
) )такой, что:
1) вектор (
overline{c}
) ортогонален векторам (
overline{a}
) и (
overline{b}
) :
(
overline{c} perp overline{a}, overline{c} perp overline{b}
)
2) векторы (
overline{a}
), (
overline{b}
) и (
overline{c}
) образуют правую тройку;
3) модуль векторного произведения равен площади параллелограмма построенного на векторах (
overline{a}
) и (
overline{b}
) :
(
|overline{c}|=|overline{a}| cdot|overline{b}| cdot sin (overline{a}, overline{b})
)
Если векторы (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) заданы своими координатами, то векторное произведение находится по формуле:
(
[overline{a}, overline{b}]=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {k} \ {a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}}end{array}right|
)
Свойства векторного произведения
1.(
[overline{a}, overline{b}]=-[overline{b}, overline{a}]
)
2.(
[overline{a}, overline{b}+overline{c}]=[overline{a}, overline{b}]+[overline{a}, overline{c}]
)
3.(
[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]
)
4.(
[overline{a}, overline{b}]=overline{0}
) если векторы (
a
) и (
overline{b}
)коллинеарные
ОПРЕДЕЛЕНИЕ
Смешанным произведением (
overline{a}
), (
overline{b}
) и (
overline{c}
) векторов называется скалярное произведение вектора (
overline{a}
) на векторное произведение векторов (
overline{b}
) и (
overline{c}
) :
(
(overline{a}, overline{b}, overline{c})=(overline{a}, overline{b} times overline{c})
)
Свойства смешанного произведения
1. Смешанное произведение равно нулю, если векторы (
overline{a}
), (
overline{b}
) и (
overline{c}
) – компланарны
2. Модуль смешанного произведения трех некомпланарных векторов (
overline{a}
), (
overline{b}
) и (
vec{C}
) равен объему параллелепипеда, построенного на этих векторах
3. Смешанное произведение векторов (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
), (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
), (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
), (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) и (
overline{c}=left(c_{1}, c_{2}, c_{3}right)
) , заданных своими координатами, равно значению определителя, составленного из координат этих векторов:
(
(overline{a}, overline{b}, overline{c})=left|begin{array}{lll}{a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}} \ {c_{1}} & {c_{2}} & {c_{3}}end{array}right|
)
4. Если тройка векторов (
overline{a}
), (
overline{b}
) и (
overline{c}
) правая, то смешанное произведение (
(overline{a}, b, overline{c})>0
) , если левая, то (
(overline{a}, overline{b}, overline{c})5.(
(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})
)
6.(
(overline{a}+d, overline{b}, overline{c})=(overline{a}, overline{b}, overline{c})+(d, overline{b}, overline{c})
)
(
(overline{a}, overline{b}, overline{c})+(overline{b}, overline{c}, overline{a},)+(overline{c}, overline{a}, overline{b})=0
)
Примеры решения задач
ПРИМЕР 1
Для векторов (
overline{a}=(3,6,-2)
) и (
overline{b}=(2,-1,5)
) найти вектор (
5 overline{a}-3 overline{b}
)
Найдем векторы
(
5 overline{a}=5 cdot(3,6,-2)=(15,30,-10)
); (
3 overline{b}=3 cdot(2,-1,5)=(6,-3,15)
)
Найдем разность:
(
5 overline{a}-3 b=(15,30,-10)-(6,-3,15)=(15-6,30-(-3),-10-15)=(9,33,-25)
)
(
5 overline{a}-3 overline{b}=(9,33,-25)
)
ПРИМЕР 2
Найти скалярное и векторное произведение векторов (
overline{a}=(1,-3,5)
) и (
overline{b}=(1,2,0)
)
Скалярное произведение векторов равно сумме произведений соответствующих координат:
(
(overline{a}, overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=1 cdot 1+(-3) cdot 2+5 cdot 0=-5
)
Векторное произведение векторов, заданных своими координатами равно
(
[overline{a}, overline{b}]=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}}end{array}right|=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {1} & {-3} & {5} \ {1} & {2} & {0}end{array}right|=-10 overline{i}+5 overline{j}+5 overline{k}
)
т.е. (
[overline{a}, overline{b}]=(-10,5,5)
)
(
(overline{a}, overline{b})=-5,[overline{a}, overline{b}]=(-10,5,5)
)
Источник